4.22. Условные экстремумы числовой функции нескольких переменных

Введем новый тип экстремумов. Для этого рассмотрим целевую функцию , для которой x и y будем считать связанными функциональной зависимостью (x, y) = 0.

Г еометрический смысл такой ситуации по казан на рис. 22.1, из которого ясно, что в этом случае можно рассматривать новый тип экстремальной задачи: найти точку ( ), лежащую на кривой (x, y) = 0, в которой функция принимает максимальное (минимальное) значение. Такого рода экстремумы называют условными экстремумами.

Если уравнение  (x, y) = 0 разрешить относительно y, то поиск условного сведется к поиску обычного экстремума для функции . Однако такая процедура часто бывает нерациональной или невозможной. Поэтому для поиска условных экстремумов был разработан специальный алгоритм – метод множителей Лагранжа, который мы сейчас рассмотрим.

Продифференцируем как сложную функцию, помня, что :

Отсюда с помощью необходимого условия экстремума получаем

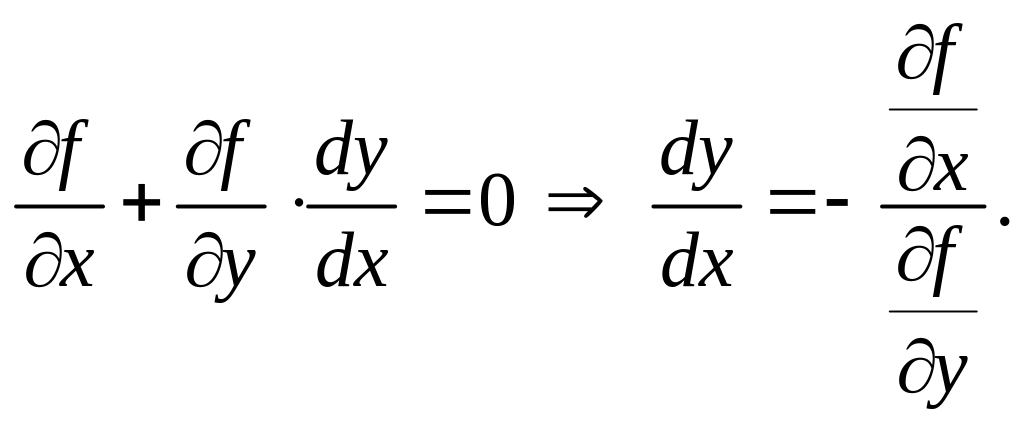(4.22.1)

С другой стороны, х и у связаны функциональной зависимостью , с помощью которой находим

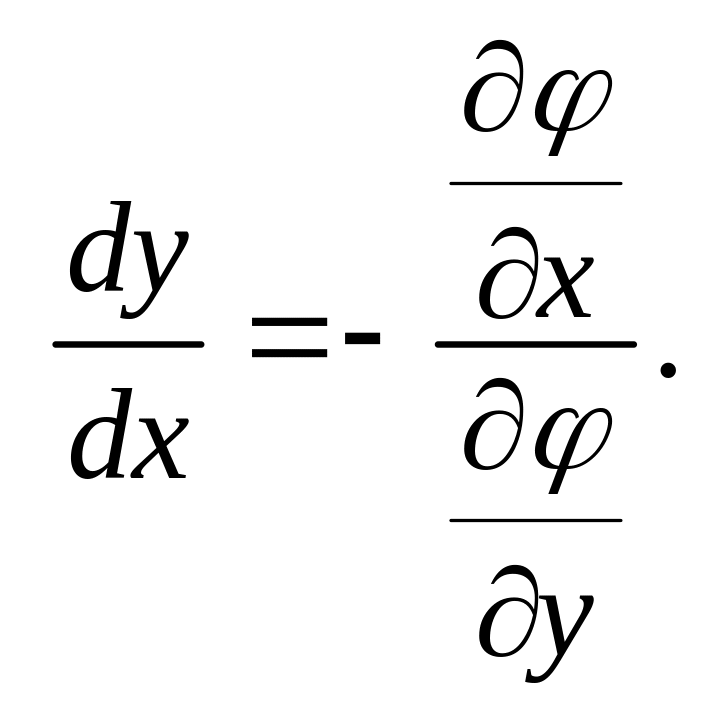(4.22.2)

Сравнивая производные (4.22.1) и (4.22.2), получаем равенство

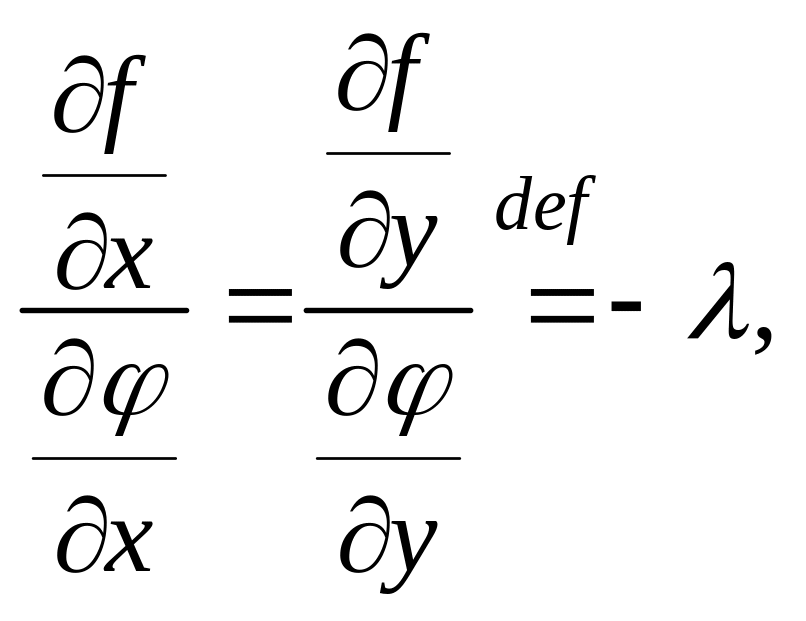
равносильное системе двух уравнений

(4.22.3)

относительно неизвестных х, у, .

Введем так называемую функцию Лагранжа:

F(x, y, )=f (x, y)+ (x, y). (4.22.4)

Тогда необходимые условия экстремума для (4.22.4)

п риводят нас к уравнениям (4.22.3) и условию  (х, у) = 0. Решая эти три уравнения, мы найдем точку условного экстремума.

Таким образом, с помощью функции Лагранжа задача о поиске условного экстремума сводится к задаче о локальных экстремумах для функции Лагранжа.

Для общего случая, когда z = f ,

функция Лагранжа строится по аналогии с (4.22.4):

П р и м е р

Найти кратчайшее расстояние от начала координат до кривой .

Целевая функция здесь имеет вид . Составляем функцию Лагранжа

,

а затем записываем необходимые условия локального экстре­мума:

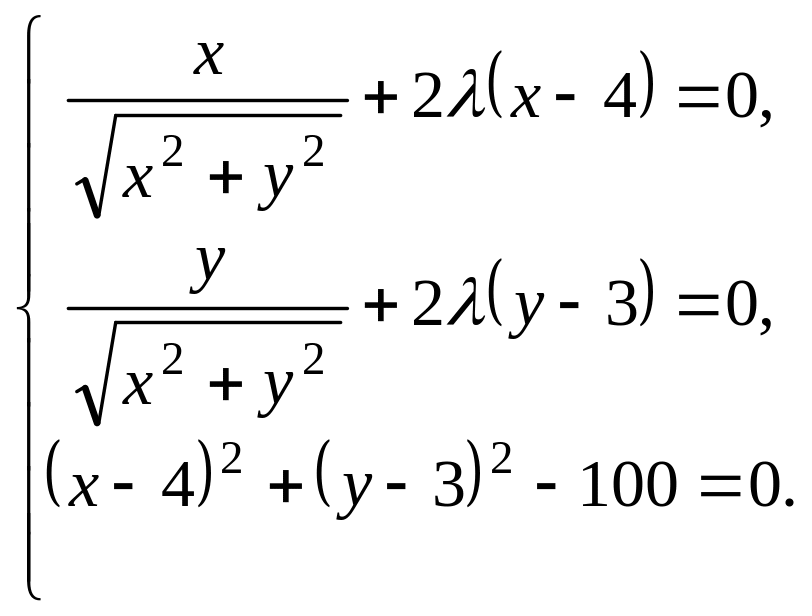(4.22.5)

Используя первые два уравнения системы (4.22.5), находим

.

Подставляем это выражение в последнее уравнение системы (4.22.5)

Интерпретация полученных результатов ясна из рис. 4.22.2: в первой точке целевая функция достигает максимума, а во второй – миниму­ма, причем

;

Достаточные условия условного экстремума используются очень редко и в нашем курсе не рассматриваются.

Задание для самостоятельного решения

1. Найти экстремумы функции z = x³ при условии

2. Найти экстремумы функции z = xy при условии 2х+3у=1.

4.23. Глобальные экстремумы числовой функции нескольких переменных

Вспомним теорему Вейерштрасса о том, что всякая непрерывная на ограниченном замкнутом множестве функция принимает на этом множестве наибольшее и наименьшее значения:

.

Говорят, что в точках M₁, М₂ функция имеет глобальные экстремумы (в точке M₁ – глобальный минимум, в точке М₂ – глобальный максимум).

В R в качестве замкнутого множества обычно рассматривается отрезок [a, b], в R² – замкнутая связная (т.е. состо­ящая из одного «куска») область на плоскости, в R³ – замкнутое тело.

Точки глобальных экстремумов могут располагаться:

1) внутри [А] (тогда они совпадают с точками локальных экстремумов);

2) на границе [А] (совпадают с точками условных экстремумов).

Рассмотрим, например, схему поиска глобальных экстремумов для функции двух переменный в криволинейном треугольнике ( см. рисунок):

1) найти точки локальных экстремумов P_i внутри [А];

2) найти точки условных экстремумов Q_i на граничных кривых _k(x, y)=0;

3) вычислить и сравнить значения целевой функции в точках P_i , Q_i и R_i .

С увеличением количе­ства переменных и усложне­нием формы множества [А] поиск глобальных экстремумов сопровождается возрастанием количества вычислений. В связи с этим для решения подобных экстремаль- ных задач частного вида разработаны специальные методы математического программирования (не путать с компьютерным программированием): линейного программирования, целочисленного программирования и т. д.