4.15. Представление некоторых функций по формуле Тейлора

Рассмотрим функцию f (x)=e^x. Ее производные выглядят особенно просто:

Формула Тейлора в окрестностях точки = 0⁹ имеет вид:

(4.15.1)

где

Можно доказать, что для т.е. функцию e^x можно аппроксимировать многочленом Тейлора с любой степенью точности при x. При этом чем выше степень, тем выше точность.

Аналогично для f (x) = cos x, = 0 получим:

(4.15.2)

где

Точно также для f (x) = sin x, = 0 имеем

(4.15.3)

где

Далее рассмотрим функцию f (x) = ln (1+x) (по-прежнему х₀ = 0):

(4.15.4)

где

В данном случае необходимо считать, что . В дальнейшем мы увидим, что здесь лишь при

Для функции f (x)= при = 0 находим:

(4.15.5)

где

Если аN, то (l + x)^а — многочлен и формула (4.15.5), начиная с некоторого слагаемого, обрывается (все последующие слагаемые и остаточный член равны нулю). Величина при и любом , если (это будет установлено позднее — в теории рядов).

Следует отметить, что разложения (4.15.1) — (4.15.5) можно использовать для вычисления значений соответствующих функций. Формулы для остаточного члена следует использовать при этом для оценки погрешностей. Такой подход широко используется при составлении компьютерных микропрограмм для вычисления значений различных функций.

Задание для самостоятельного решения

1. Написать формулу Тейлора для функции в точке = 2. Построить графики данной функции и ее многочлена Тейлора третьей степени.

2. Многочлен разложить по степеням двучлена (x + 1).

3. Аппроксимировать функции многочленами четвертой степени относительно х, определить возникающую погрешность и установить, при каких значениях х она может быть сколь угодно малой.

4. Записать формулу Тейлора ( = 0) для функций tg x; xcosx; ln(1– x + x²).

4.16. Приложения формулы Тейлора к исследованию функций

Формула Тейлора — одно из крупнейших открытий математики. Она позволяет представлять произвольную функцию в виде многочлена плюс остаточный член, который в достаточно малой окрестности точки не играет существенной роли. Напомним, что (остаточный член в форме Пеано). В связи с этим многие свойства произвольной функции можно свести к изучению свойств многочлена, которые хорошо исследованы. Рассмотрим наиболее важные примеры использования формулы Тейлора, которыми, конечно, не ограничиваются ее приложения.

4.16.1. Главная часть бм

Пусть функция имеет в точке все производные нужного порядка и . Тогда при x = функция является БМ и ее можно представить в виде

(4.16.1)

Если f ' (x₀)0, то главная часть совпадает с первым слагаемым правой части равенства (4.16.1); если , но , то — со вторым и т.д. Таким образом, главная часть БM равна

где m — наименьший порядок производной, которая отлична от нуля, т.е. при xx₀

(4.16.2)

Напомним, что главная часть БМ определяется неоднозначно. Здесь она представлена наиболее просто — в виде степенной функции.

Например, для функции

f (x) = tg x – x

при x0 имеем:

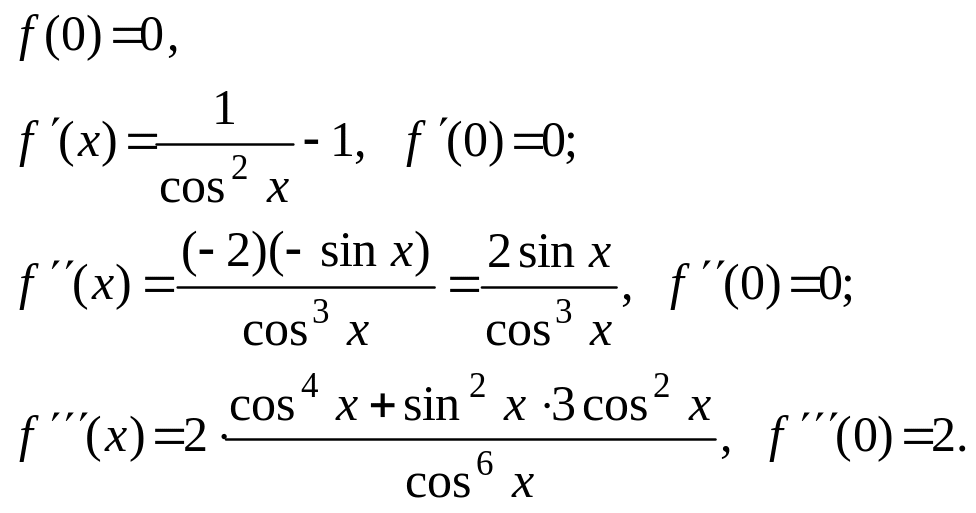
Таким образом, по формуле (4.16.2) получим

tg x – x