Глава пятая. Интегральное исчисление для числовой функции одной переменной.
Первообразная и неопределенный интеграл.
Пусть дана функция
Тогда производная
Оператор, сопоставляющий функции её
производную, называется, как известно,
оператором дифференцирования D
:
Рассмотрим обратную задачу: зная функцию
найти функцию
,
производная которой равна
(5.1.1)
Говорят, что функция F(x) является первообразной для функции f(x).
П р и м е р:
Из последнего примера следует, что задача об отыскании первообразной не имеет единственного решения.
Теорема 1 (о виде первообразных). Любые две первообразные для одной и той же функции различаются лишь на постоянную величину.
Доказательство:
Последняя
импликация получается с помощью теоремы
Лагранжа: если
для всех
то
для любых
Таким образом, любая первообразная для заданной функции имеет вид
здесь
-
какая-либо первообразная, С –
произвольная постоянная.
Общий вид первообразных для функции f(x) называется неопределённым интегралом от функции f(x):
(5.1.2.)
В (5.1.2.) f(x) называется подынтегральной функцией, f(x)dx – подынтегральным выражением.
Геометрический смысл неопределённого интеграла ясен из рис. 5.1, где показано множество кривых, каждая из которых может быть получена сдвигом одной кривой y=F(x) в направлении оси ординат. Неопределённый интеграл есть произвольный элемент y=F(x)+С указанного семейства.
y
0
y=F(x)
x
Рис. 5.1
Процедура вычисления неопределённого интеграла называется интегрированием функции f(x).
На неопределённый
интеграл можно смотреть как на оператор,
действующий из С в
Оператор интегрирования иногда обозначают следующим образом:
имея ввиду, что если заменить точку функцией f(x), то получится значение оператора на функции f(x).
Теорема 2 (о существовании неопределённого интеграала).
Для всякой функции класса
существует неопределённый интеграл на
том же отрезке
.
В данном курсе доказательство этой теоремы не рассматривается.
5.2.Основные свойства неопределённого интеграла.
Производная от неопределённого интеграла равна подынтегральной функции:
(5.2.1)
Доказательство:
Дифференциал от неопределённого интеграла равен подынтеграль-ному выражению:
(5.2.2)
Доказательство:
Неопределённый интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная:
(5.2.3)
Доказательство:
Постоянный множитель можно выносить за знак неопределённого интеграла:
(5.2.4)
Знак равенства в (5.2.4) понимается как совпадение производных для левой и правой частей. Отсюда следует очень простое доказательство:
Неопределённый интеграл от суммы функций равен сумме интегралов от этих функций, если интегралы существуют:
(5.2.5)
Доказательство:
Из равенств (5.2.4), (5.2.5) следует, что оператор интегрирования является линейным оператором.
Таблица основных интегралов.
Приведём основные формулы для интегрирования элементарных функций. Часть этих формул известна из школьного курса математики.
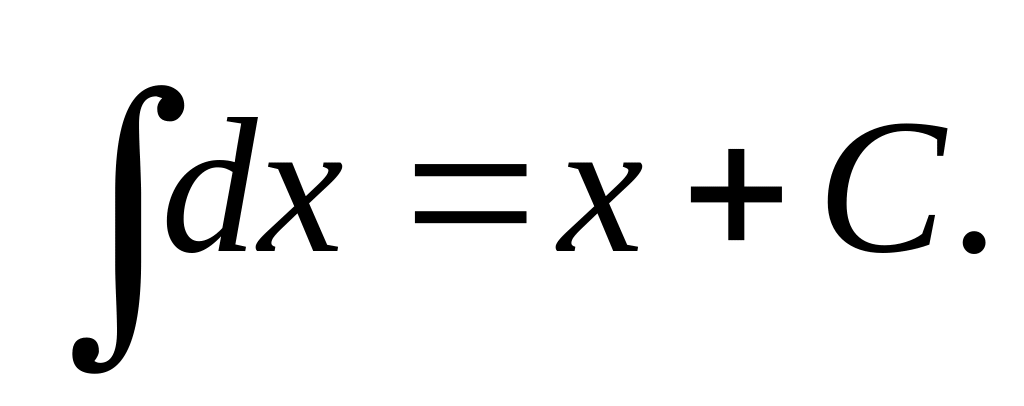
Частный случай
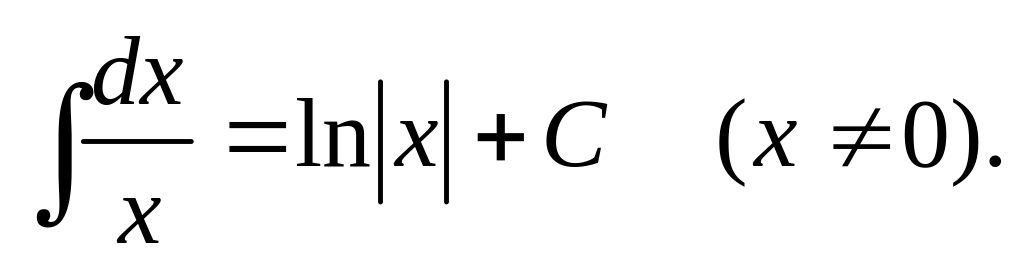
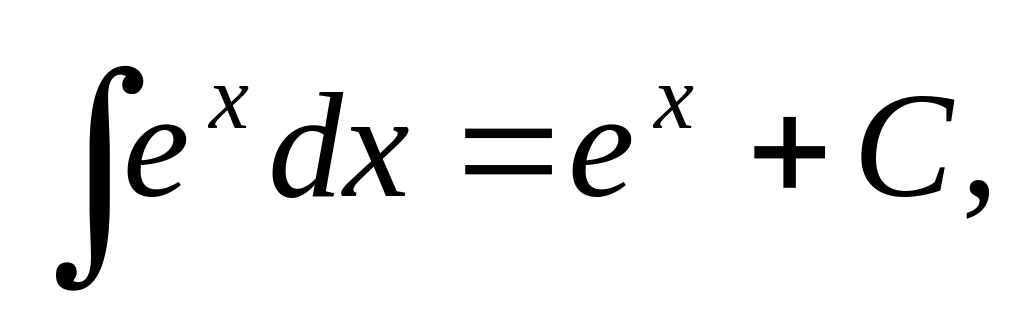
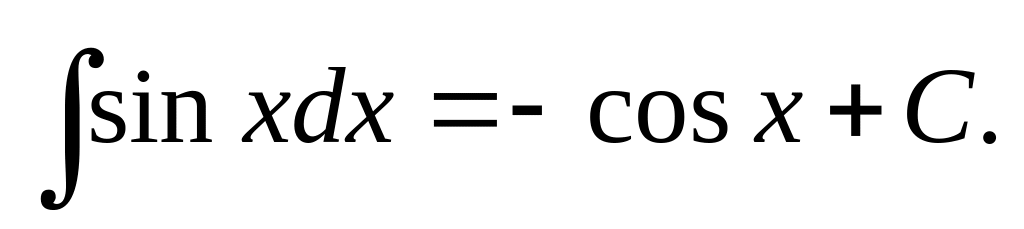
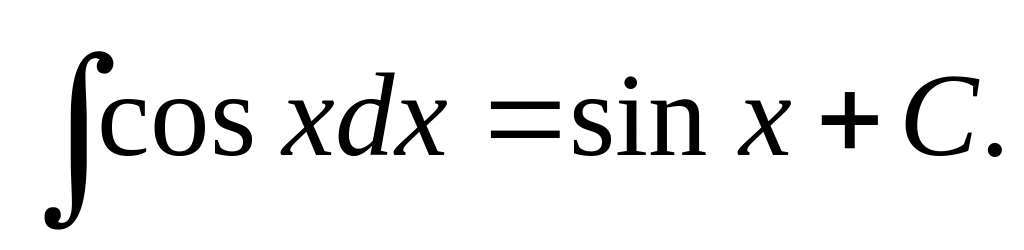
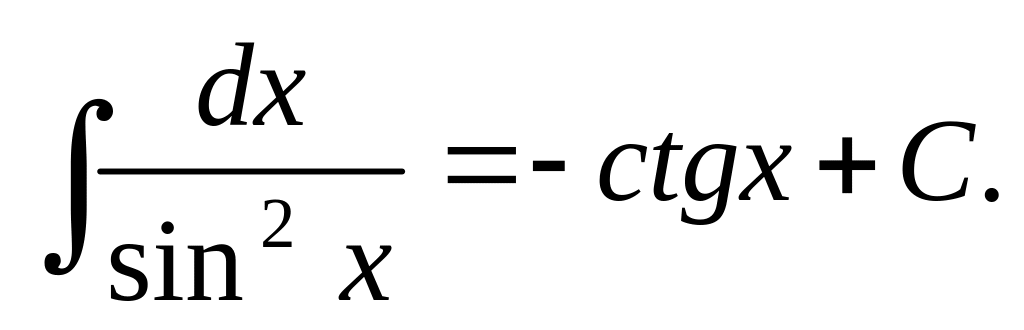
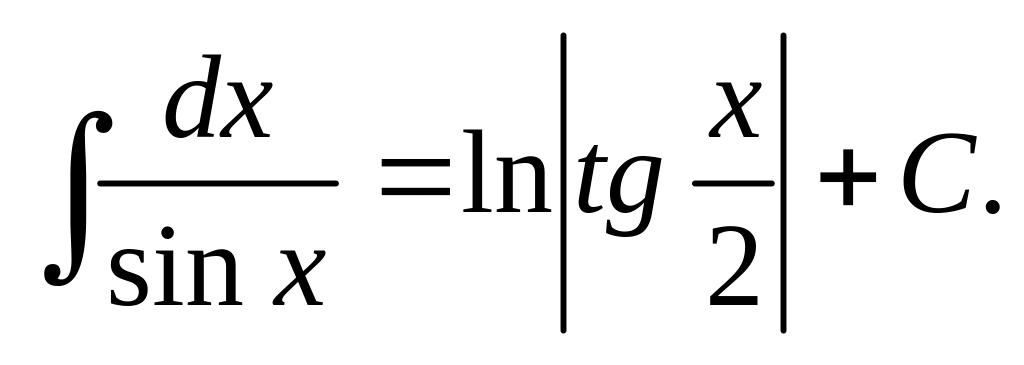
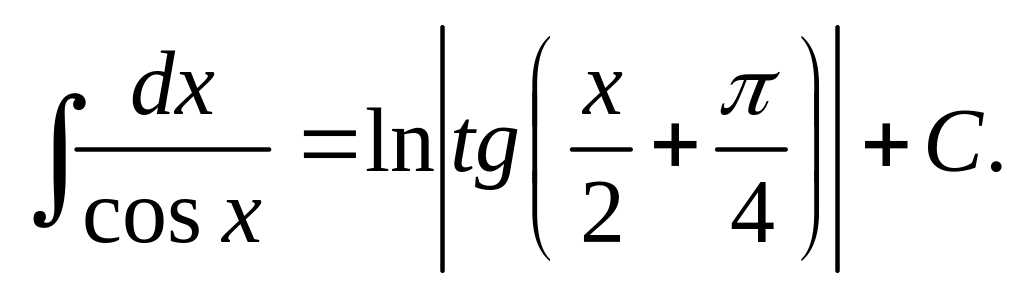
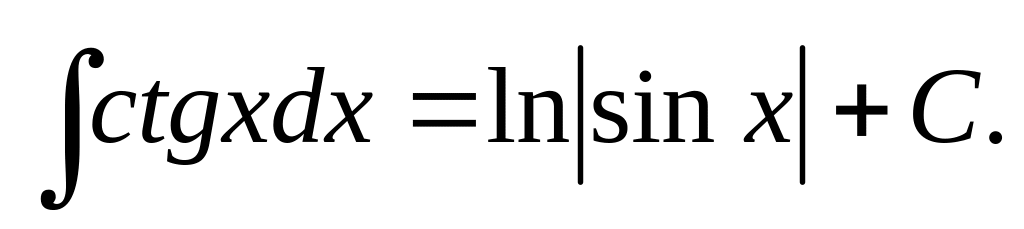
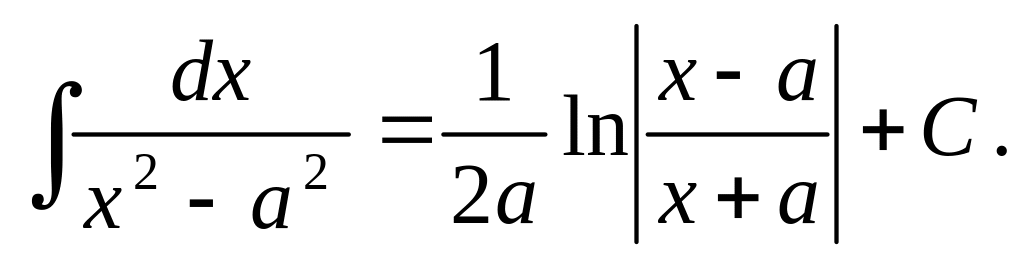
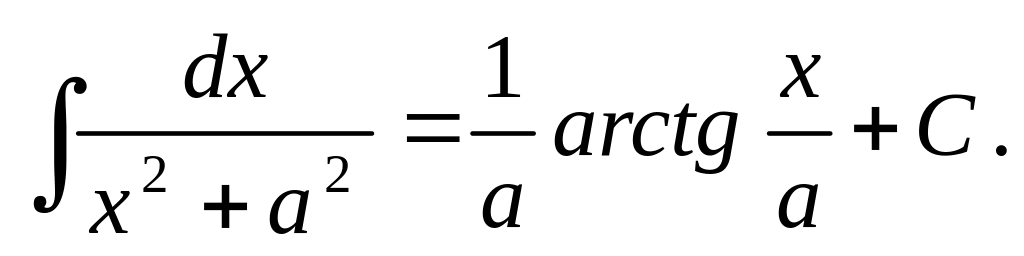
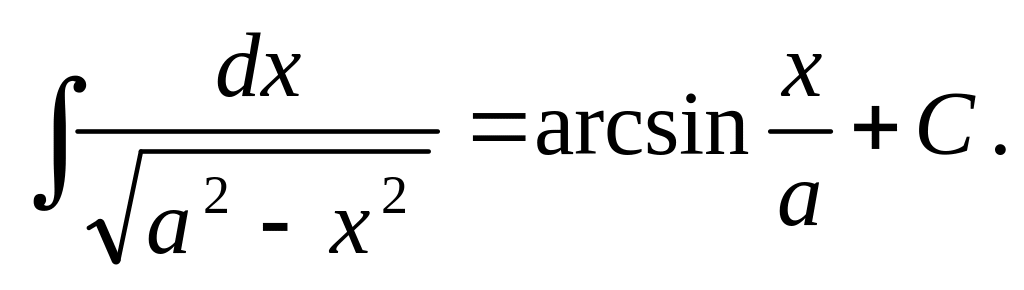
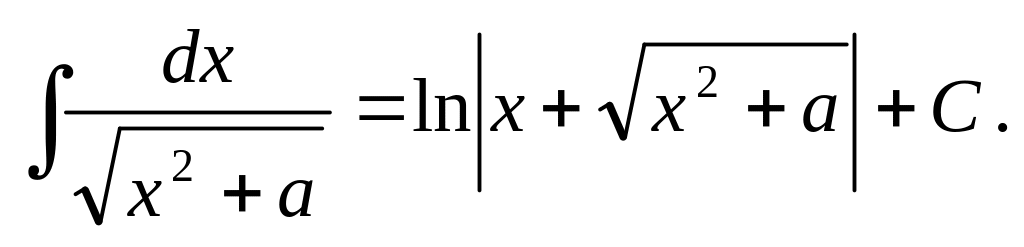
Приведенные формулы проверяют с помощью дифференцирования. Например, проверим формулу 15:
Аналогично убеждаемся в справедливости формулы 3:
.
В качестве упражнения докажите справедливость формул 13,14, 16.
Задание для самостоятельного решения.
Вычислите следующие интегралы:
1.
2.
3.
4.
5.
6.
7.
8.
9.
