
- •4.12. Кривизна плоской кривой. Эволюта и эвольвента
- •4.13. Формула Тейлора7
- •Вопросы
- •4.14. Остаточный член формулы Тейлора в форме Лагранжа
- •4.15. Представление некоторых функций по формуле Тейлора
- •4.16. Приложения формулы Тейлора к исследованию функций
- •4.16.1. Главная часть бм
- •Вопросы
- •4.16.2 Возрастание и убывание функции
- •4.16.3. Экстремумы функции
- •4.16.4. Выпуклость и вогнутость кривой
- •4.16.5. Точки перегиба кривой
- •Вопросы
- •4.17. Формула Тейлора для числовой функции нескольких переменных
- •4.18. Локальные экстремумы функции нескольких переменных
- •4.19. Аппроксимация опытных данных по методу наименьших квадратов
- •4.20. Производная скалярного поля по направлению. Градиент
- •Вопросы
- •Задание для самостоятельного решения
- •4.21. Понятие о приближенных методах поиска локальных экстремумов
- •4.21.1. Релаксационный13 метод
- •4.21.2. Градиентный метод
- •4.21.3. Метод крутого восхождения (наискорейшего спуска)
- •4.21.4. Метод последовательного поворота симплекса
- •4.22. Условные экстремумы числовой функции нескольких переменных
- •4.23. Глобальные экстремумы числовой функции нескольких переменных
- •Задание для самостоятельного решения
- •4.24. Формулировка задачи линейного программирования
- •4.25. Понятие о задачах нелинейного и целочисленного программирования
- •4.26. Дифференциал и производная вектор-функции скалярного аргумента
- •Задание для самостоятельного решения
- •4.27. Кривизна пространственной кривой
- •Вопросы
- •Задание для самостоятельного решения
Вопросы
Каковы главные части БМ, определяемые с помощью формулы Тейлора:
1) cosx – 1; 2) sinx – x; 3) ln (1+ x) – x; 4) (l + x)а–1–аx ?
Задание для самостоятельного решения
1. Вычислить пределы с помощью выделения главной части функций по формуле Тейлора:
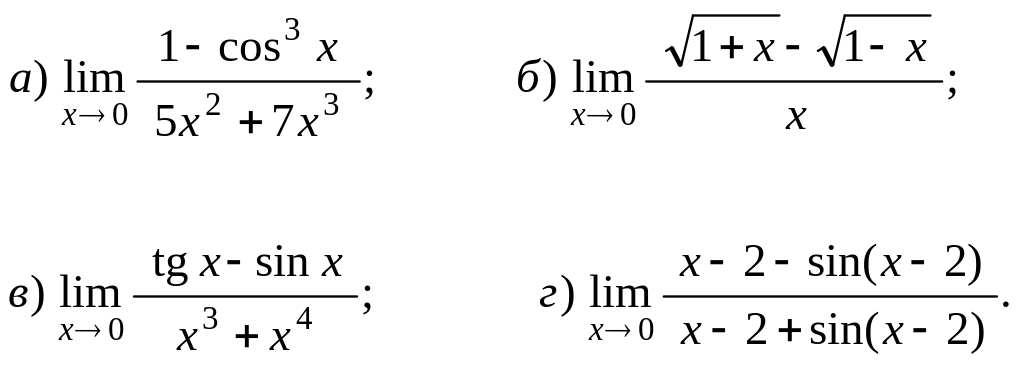
4.16.2 Возрастание и убывание функции
Пусть
![]() 0,
тогда
0,
тогда
![]()
Таким образом, в окрестности
точки
произвольная функция
аппроксимируется линейной функцией,
причем степень аппроксимации тем выше,
чем х ближе к
.
Отсюда ясно, что при
> 0 функция
в окрестности точки
![]() возрастает,
а при
<
0 убывает (рис.
4.16.1). Если
=
0, то точка
называется стационарной. Такие
точки мы рассмотрим особо.
возрастает,
а при
<
0 убывает (рис.
4.16.1). Если
=
0, то точка
называется стационарной. Такие
точки мы рассмотрим особо.

4.16.3. Экстремумы функции
Пусть
=
0, а
![]()
0. Тогда вблизи точки
0. Тогда вблизи точки
![]()
Так как
![]()
0, то знак разности f
(x) –
0, то знак разности f
(x) –![]() всецело определяется знаком второй
производной
:
всецело определяется знаком второй
производной
:
![]()
Аналогично рассматривается случай, когда
![]()
Здесь вблизи точки x0
![]() (4.16.3)
(4.16.3)
Неизменность знака правой части равенства
(4.16.3) возможна лишь в том случае,
когда m —
четное число. Поэтому справедлив
следующий вывод: если наименьший порядок
m производной, отличной
от нуля в точке
,
является четным, то в точке
функция имеет экстремум (при
![]() >
0 — минимум, при
)
< 0 — максимум). Если m
— нечетное число, то экстремума в
точке
не будет (рис. 4.16.2).
>
0 — минимум, при
)
< 0 — максимум). Если m
— нечетное число, то экстремума в
точке
не будет (рис. 4.16.2).

Пусть, например, требуется найти экстремум функции
![]() .
.
Для решения этой задачи последовательно вычисляем
![]() ;
;
![]() ;
;
![]()
Результат можно было предвидеть, если
учесть, что
![]() .
.
4.16.4. Выпуклость и вогнутость кривой
 Рассмотрим
кривые, изображенные на рис.
4.16.3. Пусть для произвольной точки
М лежащей на кривой, построена
касательная к этой кривой. Если обозначить
ординату точки на кривой через yкр,
а соответствующей (т.е. имеющей ту же
абсциссу
Рассмотрим
кривые, изображенные на рис.
4.16.3. Пусть для произвольной точки
М лежащей на кривой, построена
касательная к этой кривой. Если обозначить
ординату точки на кривой через yкр,
а соответствующей (т.е. имеющей ту же
абсциссу![]() )
точки на касательной —
через yкас,
то можно рассмотреть разность
)
точки на касательной —
через yкас,
то можно рассмотреть разность
![]() (4.16.4)
(4.16.4)
Если > 0
для любых
![]() (a, b),
,
то это означает, что на интервале (a, b)
кривая лежит «не ниже» любой из своих
касательных. Такая кривая называется
вогнутой (выпуклой вниз) (рис.
4.16.3 а). Если
< 0, то кривая называется выпуклой
(выпуклой вверх) (рис. 4.16.3 б).
(a, b),
,
то это означает, что на интервале (a, b)
кривая лежит «не ниже» любой из своих
касательных. Такая кривая называется
вогнутой (выпуклой вниз) (рис.
4.16.3 а). Если
< 0, то кривая называется выпуклой
(выпуклой вверх) (рис. 4.16.3 б).
Оказывается, что знак выражения (4.16.4) очень просто устанавливается с помощью формулы Тейлора:
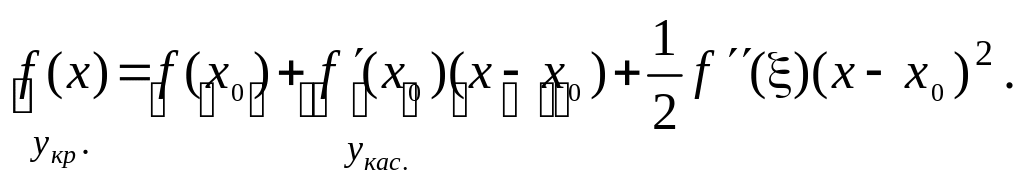 (4.16.5)
(4.16.5)
Из (4.16.5) сразу следует,
что при
![]()
![]()
откуда имеем
![]() вогнутость
вогнутость
![]() ;
;
![]() выпуклость
выпуклость
![]() .
.
4.16.5. Точки перегиба кривой
Точку, лежащую на кривой10 называют точкой перегиба, если она отделяет участок выпуклости кривой от участка вогнутости (рис. 4.16.4).
 Если
функция
Если
функция
![]() ,
т.е. дважды непрерывно дифференцируема,
то по одну сторону от точки перегиба f
''(х) < 0, а по другую f
''(х) > 0. Следовательно, для абсциссы
точки перегиба
,
т.е. дважды непрерывно дифференцируема,
то по одну сторону от точки перегиба f
''(х) < 0, а по другую f
''(х) > 0. Следовательно, для абсциссы
точки перегиба
![]() имеем
=0.
Таким образом, точки перегиба находятся
среди точек с такими абсциссами
,
для которых
=
0 или
не существует.
имеем
=0.
Таким образом, точки перегиба находятся
среди точек с такими абсциссами
,
для которых
=
0 или
не существует.
Это условие является необходимым, но не достаточным. Достаточное условие состоит в том, чтобы производная f "(x) при переходе через значение изменяла свой знак.
Очевидно, что кривая в точке перегиба
переходит с одной стороны касательной
на другую, т.е. величина
![]() должна изменять свой знак. Поскольку
должна изменять свой знак. Поскольку
 то
то
![]()
Если
![]() 0,
то
0,
то
![]() и
изменяет знак при переходе х через
значение
и
изменяет знак при переходе х через
значение
![]() ,
т.е. имеем точку перегиба с абсциссой
.
,
т.е. имеем точку перегиба с абсциссой
.
Если
=0,
![]() ,
то
знака не изменяет и точки перегиба не
будет:
,
то
знака не изменяет и точки перегиба не
будет:
![]()
Отсюда ясно, что достаточное условие
точки перегиба состоит в том, что младшая
из производных
![]() ,
отличных от нуля, имеет
нечетный порядок. Это согласуется с уже
выполненным анализом стационарных
точек: если m
— четное, то в стационарной точке
будет экстремум, если m
— нечетное, то стационарная точка
отвечает точке перегиба.
,
отличных от нуля, имеет
нечетный порядок. Это согласуется с уже
выполненным анализом стационарных
точек: если m
— четное, то в стационарной точке
будет экстремум, если m
— нечетное, то стационарная точка
отвечает точке перегиба.
П р и м е р
![]() .
.
Находим абсциссы возможных точек перегиба:
![]() .
.
Проверяем это значение:
![]() ,
,
т.е. = 0 отвечает точке перегиба.
