5.7. Формула Ньютона-Лейбница.

Формула, найденная Ньютоном и Лейбницем (независимо друг от друга), устанавливает связь между определённым и неопределённым интегралами. Она позволяет эффективно вычислять определенные интегралы и является основной формулой интегрального исчисления.

Для введенного ранее разбиения отрезка на n частей

очевидно, справедливо равенство

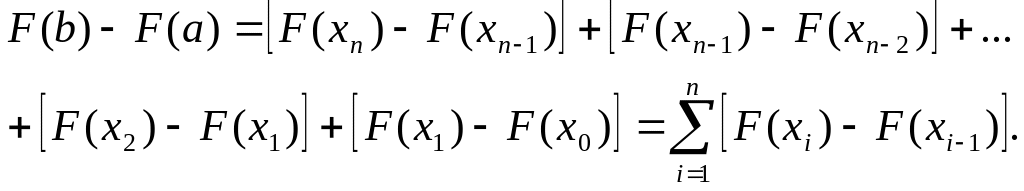(5.7.1)

Пусть Тогда по формуле Лагранжа

и формуле (5.7.1) можно придать вид

(5.7.2)

Формула (5.7.2) показывает, что при соответствующем выборе точек величина интегральной суммы при любом n постоянна и равна Поэтому при получим

(5.7.3)

(5.7.3) называют формулой Ньютона-Лейбница.

Для обозначения приращения функции часто используют знак двойной подстановки

П р и м е р. Вычислить площадь криволинейной трапеции, ограниченной кривой

Решение таково:

Задание для самостоятельного решения.

1. Вычислить интегралы:

2. Вычислить площади фигур, ограниченных линиями:

а)

б)

в)

3. Вычислить интеграл 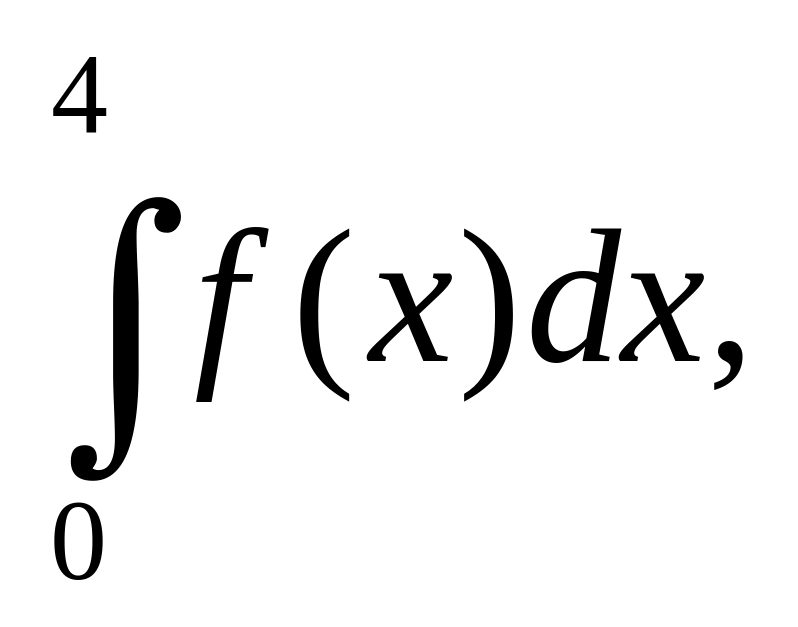если

а) б)

5.8. Основные свойства определённого интеграла.

1) Определенный интеграл является линейным функционалом

т.е. (5.8.1)

(5.8.2)

где

Равенство (5.8.1) вытекает из очевидного свойства соответствующих интегральных сумм

Аналогично проверяется равенство (5.8.2):

2. Изменение обозначения переменной интегрирования не отражается на величине определенного интеграла:

(5.8.3)

Поэтому переменную интегрирования в определенном интеграле называют «немой» по аналогии с «немыми» индексами суммирования, не попадающими в конечный результат.

(индекс i здесь “немым” не является).

Равенство (5.8.3) очевидно из структуры формулы для интегральной суммы (5.6.1).

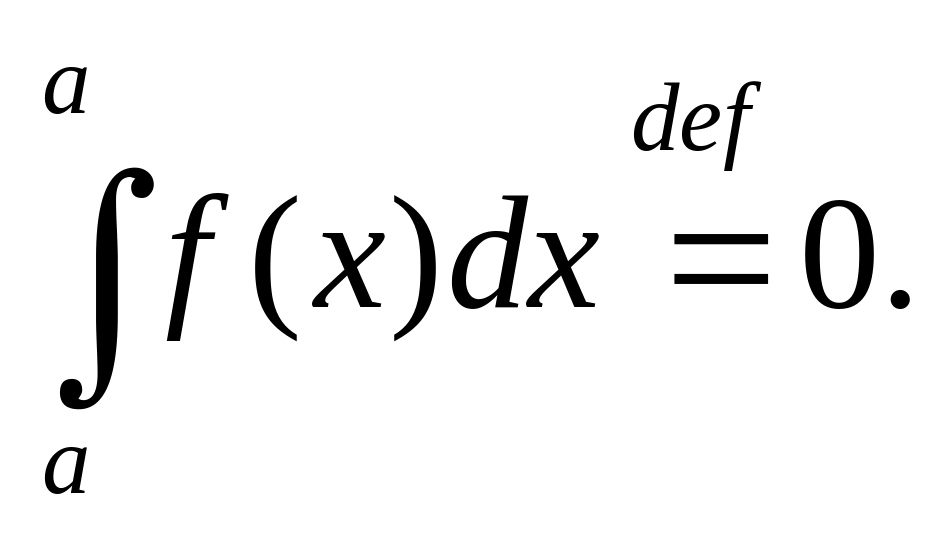2. (5.8.4)

Равенство (5.8.4) следует понимать как естественное определение интеграла по «отрезку нулевой длины»:

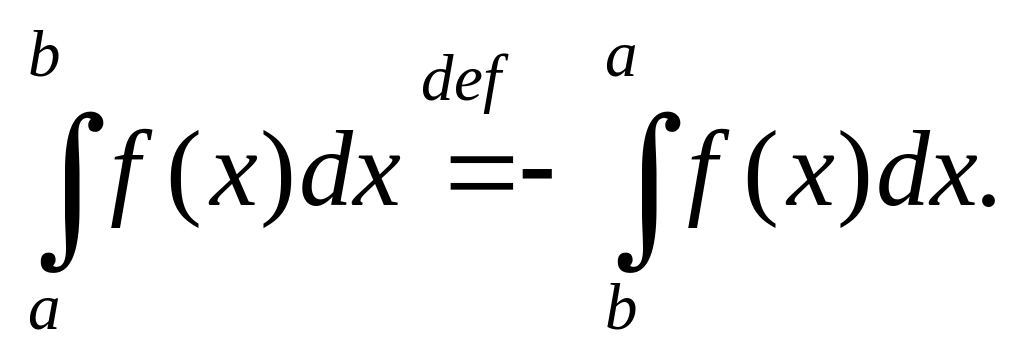2. (5.8.5)

Формула (5.8.5) представляет собой определение интеграла по направленному отрезку Это определение целесообразно принять в связи с формулой Ньютона-Лейбница, распространив последнюю на случай любых пределов интегрирования:

5) (5.8.6)

Говорят, что равенство (5.8.6) выражает аддитивность определённого интеграла относительно области интегрирования: значение интеграла на равно сумме его значений на причём Ø.

Доказательство нетрудно выполнить, записав соответствующие интегральные суммы. Однако, в данном случае мы воспользуемся формулой Ньютона-Лейбница:

Формула (5.8.6) с учетом определения (5.8.5) справедлива не только для В ней a, b, c могут быть любыми действительными числами (лишь бы существовали все рассматриваемые интегралы).