
- •Глава пятая. Интегральное исчисление для числовой функции одной переменной.
- •Первообразная и неопределенный интеграл.
- •5.2.Основные свойства неопределённого интеграла.
- •Интегрирование подстановкой.
- •5.5. Интегрирование по частям.
- •5. 6. Понятие определенного интеграла как предела интегральной суммы.
- •5.7. Формула Ньютона-Лейбница.
- •5.8. Основные свойства определённого интеграла.
- •5.9. Оценки определенного интеграла.
- •5.10. Теорема о среднем значении.
- •5.11. Вычисление определённых интегралов с помощью подстановки.
- •5.12. Вычисление определённых интегралов путём интегрирования по частям.
- •5.13. Практическая схема применения определенных интегралов для решения прикладных задач.
- •5.13.1. Вычисление площадей плоских областей.
- •5.13.2. Вычисление длины дуги плоской кривой.
- •5.13.3. Вычисление объёма и площади поверхности тела вращения.
- •5.13.4 Вычисление объёма тела с заданными площадями параллельных сечений.
- •5.14. Примеры физических приложений определённых интегралов.
- •5.15. Приближениое вычисление определённых интегралов.
- •5.15.1. Формула прямоугольников.
- •5.15.2. Формула трапеций.
- •5.15.3. Формула парабол.
- •5.16. Несобственные интегралы.
- •5.16.1. Несобственные интегралы с бесконечными пределами интегрирования
- •5.16.2 Несобственные интегралы от разрывных функций.
- •5.16.3. Теоремы о сходимости несобственных интегралов
- •Интеграл как функция пределов интегрирования. Понятие о специальных функциях, определяемых интегралами с переменным верхним пределом.
- •5.18. Понятие об интегралах, зависящих от параметра
- •5.19. Понятие о гамма-функции
- •Комплексные числа.
- •5.1. Основные понятия о комплексных числах.
- •5.2. Запись комплексных чисел в тригонометрической и
- •5.3. Разложение многочлена на множители в случае действительных и мнимых корней.
- •5.4. Разложение правильной рациональной дроби на простейшие дроби
- •Глава шестая. Кратные, криволинейные и поверхностные интегралы; элементы теории поля.
- •Понятие об интеграле по замкнутой ограниченной области
Интегрирование подстановкой.
Выполним в
интеграле
![]() формальную замену переменной интегрирования
формальную замену переменной интегрирования
![]()
![]() (5.4.1)
(5.4.1)
Проверим полученную формулу, вычислив производные по x от левой и правой частей равенства:
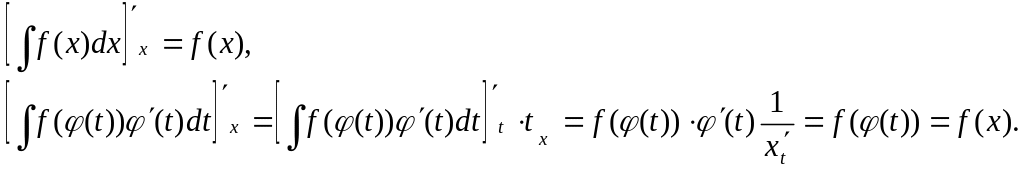
Таким образом, формула (5.4.1) доказана. При этом считалось, что
![]()
Формула (5.4.1) выражает метод
интегрирования подстановкой, или
метод замены переменной интегрирования.
Этот метод целесообразно использовать
в тех случаях, когда интеграл в правой
части равенства (5.4.1) проще, чем в левой
части. После вычисления нового интеграла
приходится возвращаться к старой
переменной, для чего находят обратную
функцию
![]()
П р и м е р:
Подстановки, использованные в приведенных примерах, весьма просты, и их следует научиться выполнять «в уме» не производя записей с переменной t.
Заметим, что формула (5.4.1) оправдывает казалось бы излишне сложное обозначение неопределённого интеграла (сравнить с обозначением производной).
Задание для самостоятельного решения.
Вычислить следующие интегралы методом подстановки:
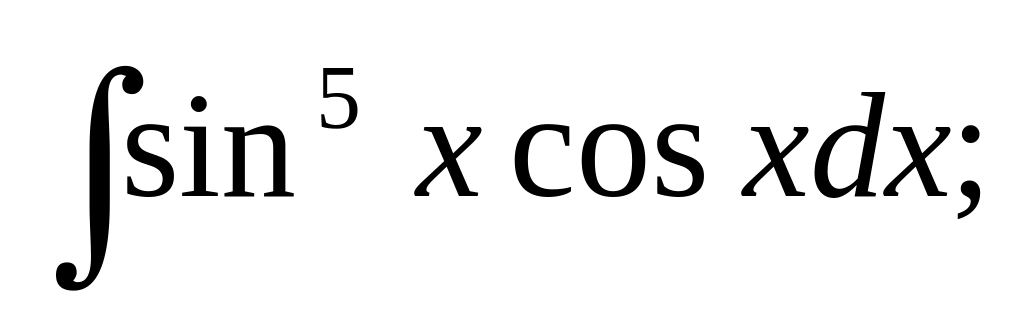
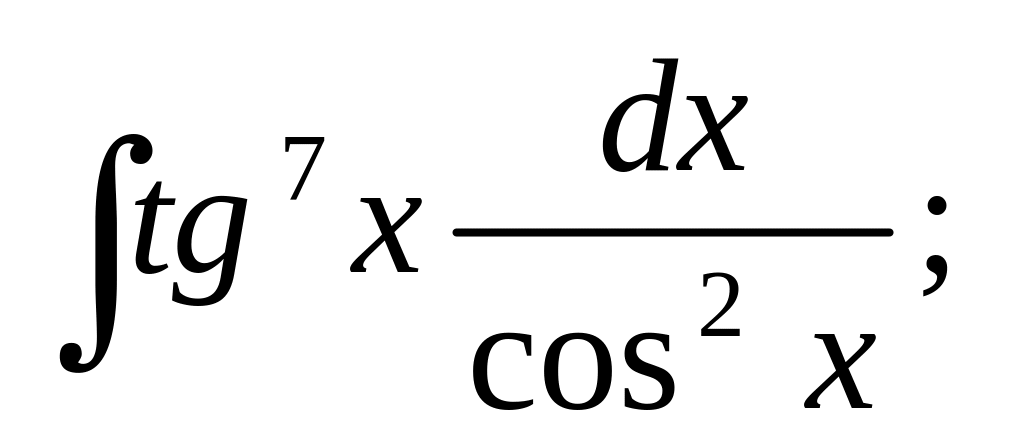
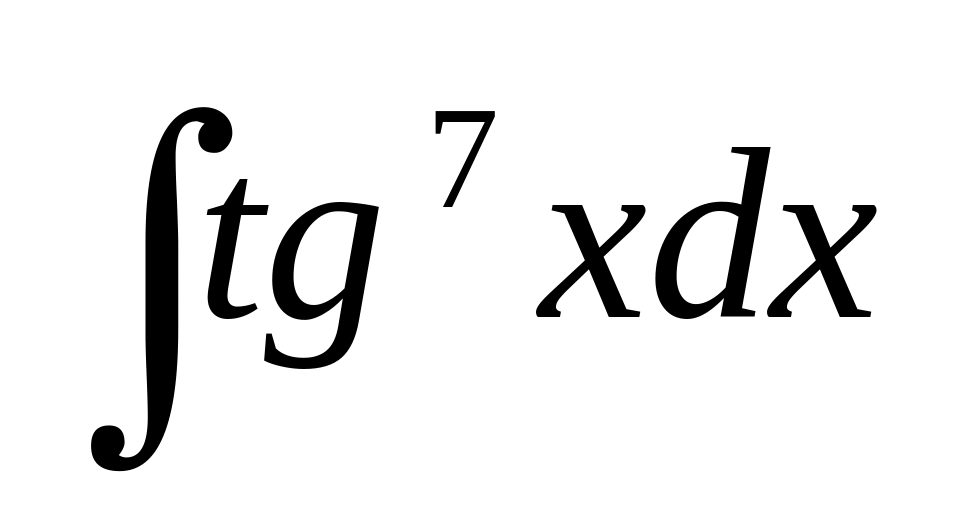 (подстановка
(подстановка
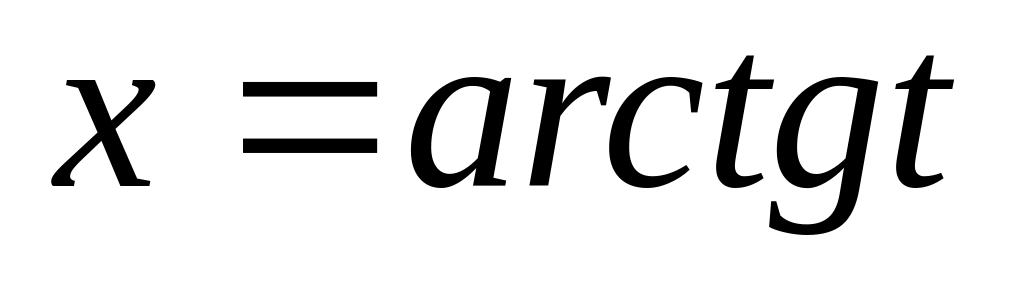 );
);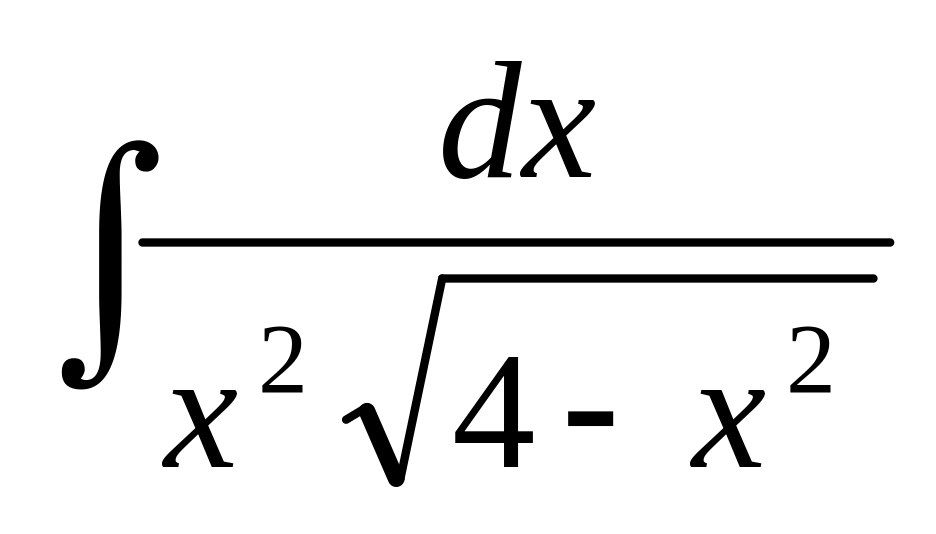 (подстановка
(подстановка
 );
);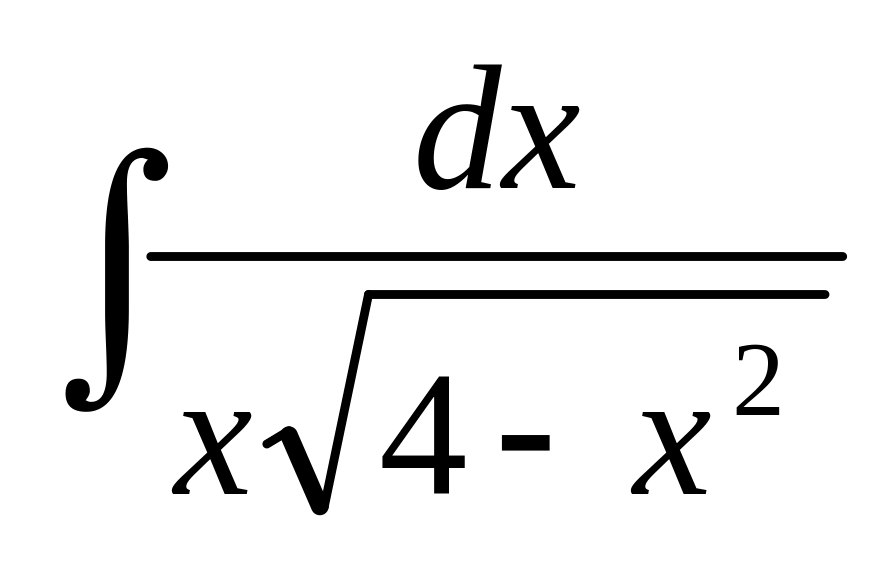 (подстановка
(подстановка
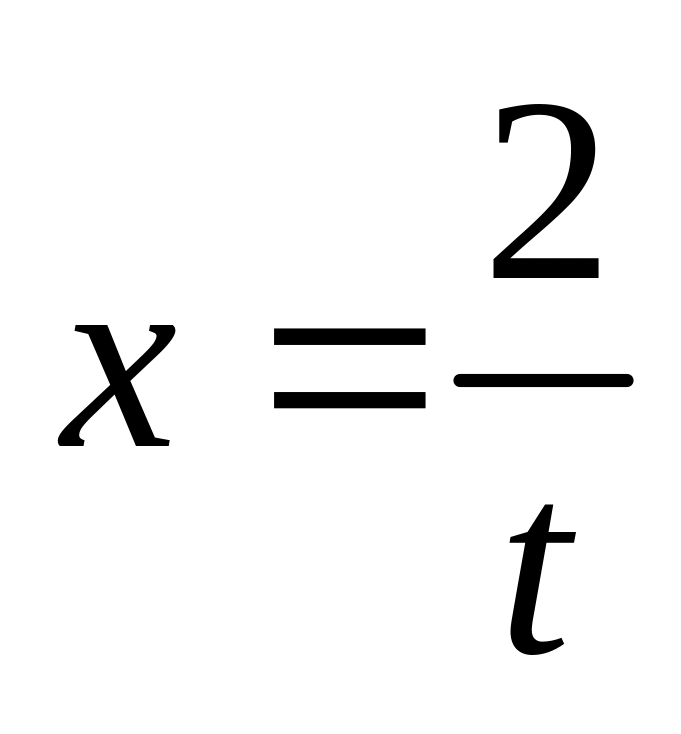 );
);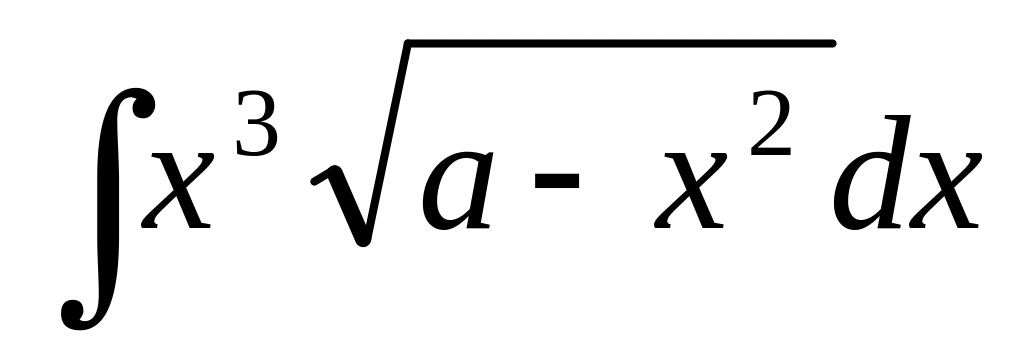 (подстановка
(подстановка
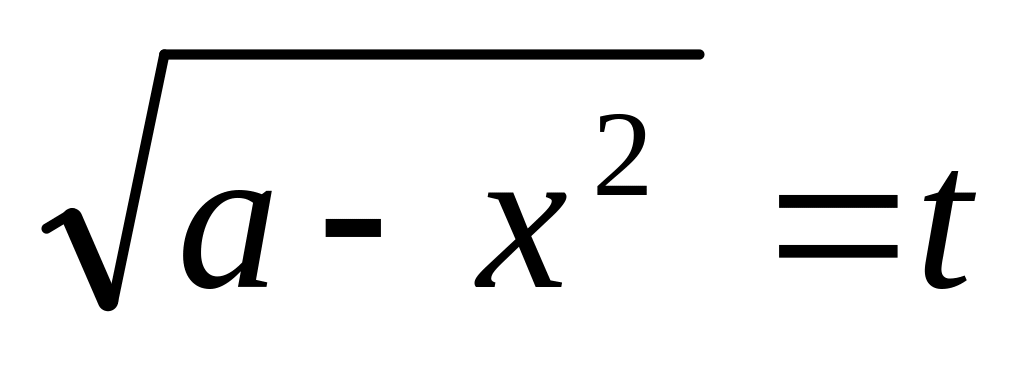 );
);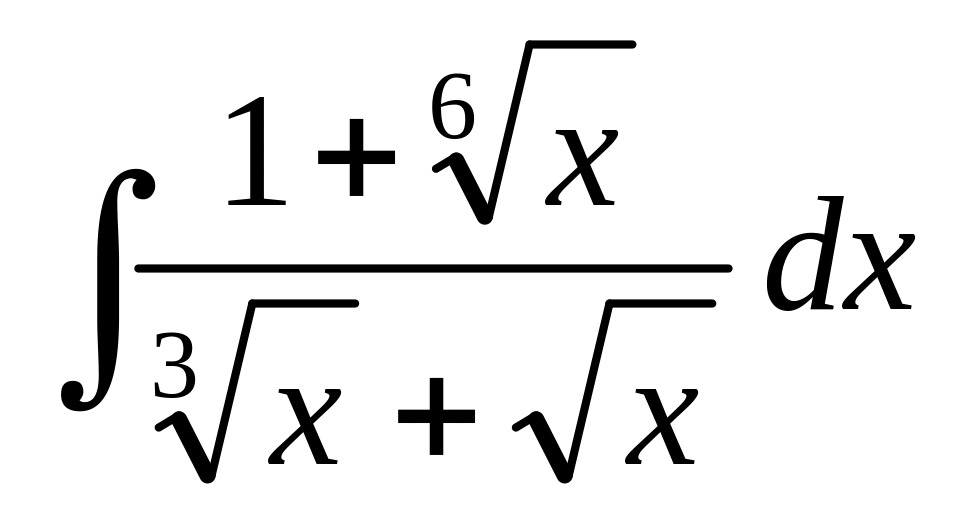 (подстановка
(подстановка
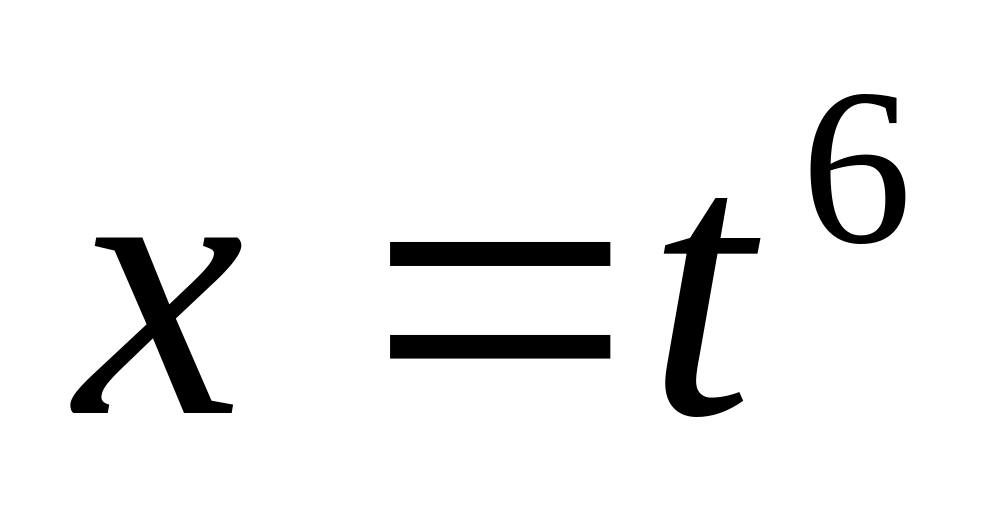 );
);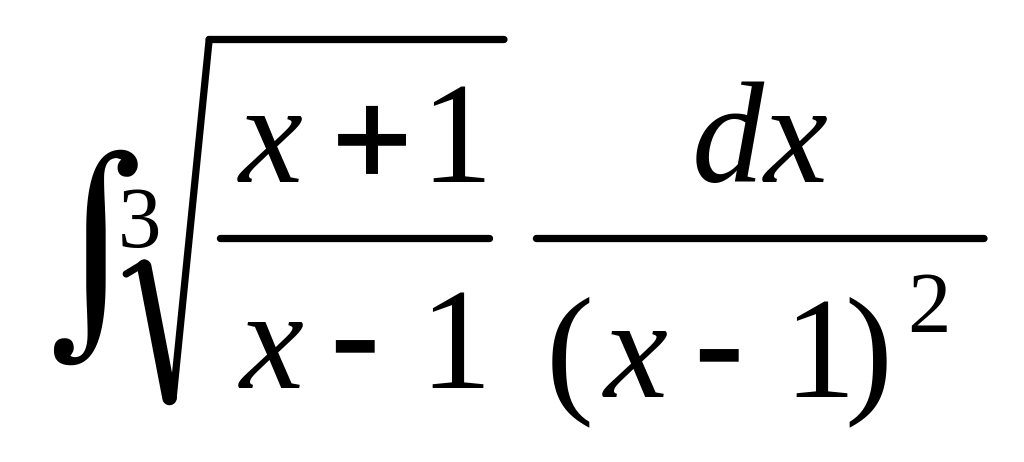 (подстановка
(подстановка
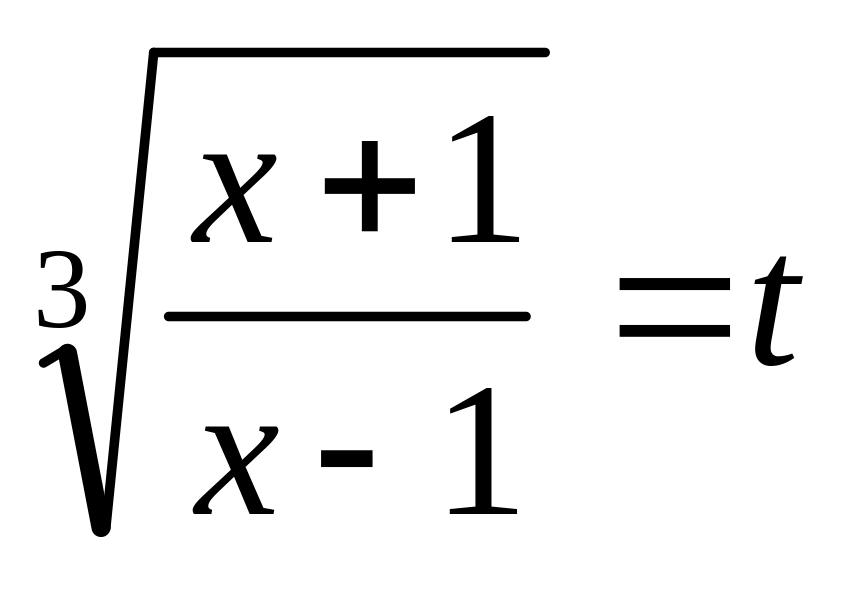 );
);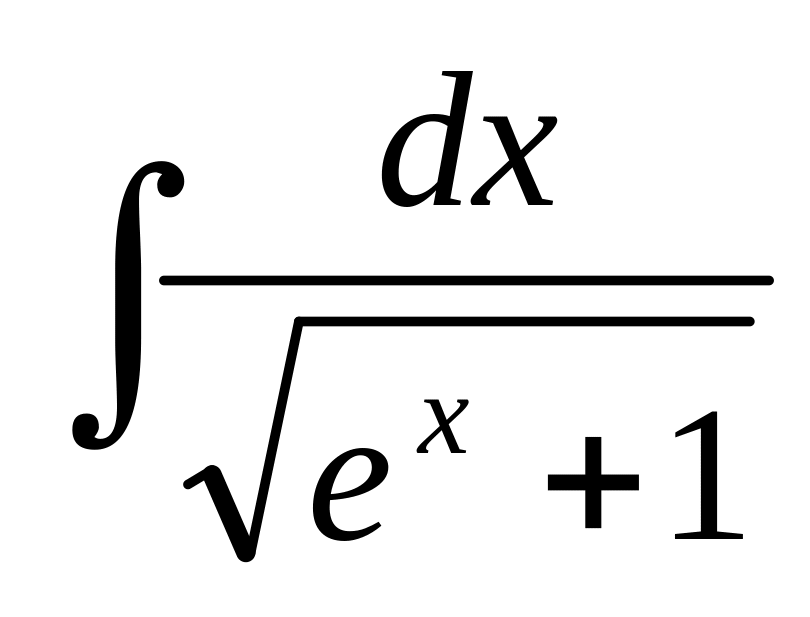 (подстановка
(подстановка
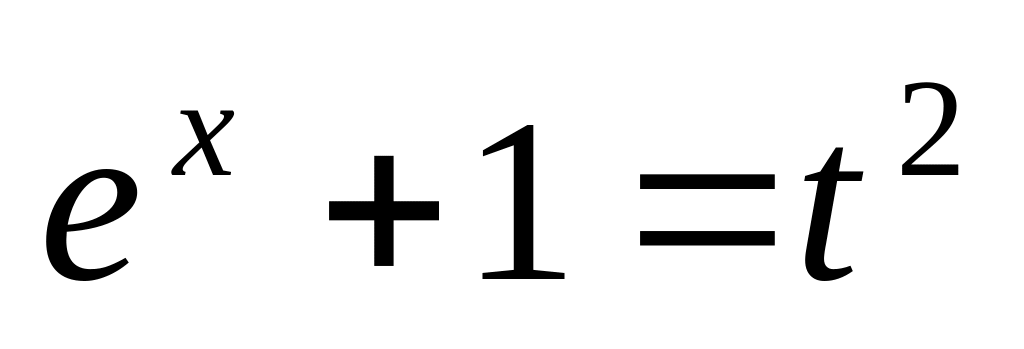 );
);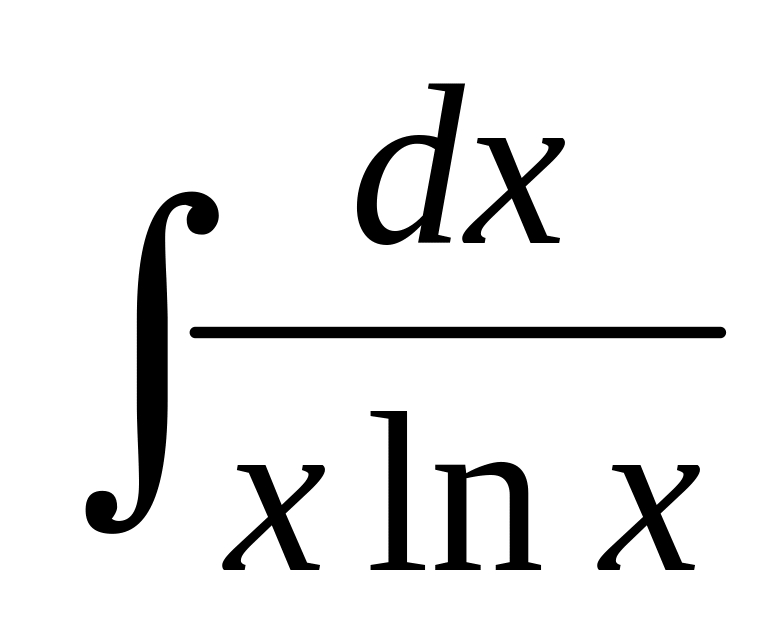 (подстановка
(подстановка
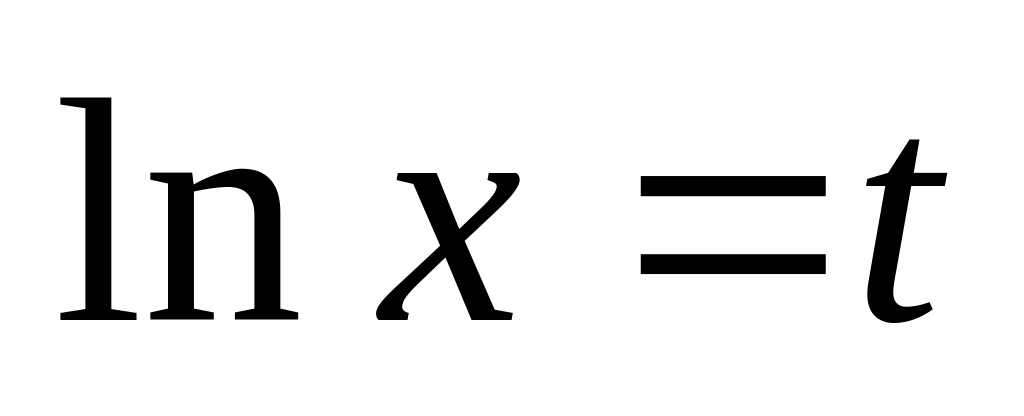 );
);
Вычислить интегралы и проверить результаты дифференцированием:
1)
![]() 2)
2)
![]()
3)
![]() 4)
4)
![]()
Используя «универсальную тригонометрическую» подстановку, вычислите интегралы:
1)
![]() 2)
2)
![]()
(подстановка
![]()
5.5. Интегрирование по частям.
Второй из основных методов интегрирования базируется на формуле, выражающей дифференциал произведения:
![]()
Отсюда имеем
![]()
или рассматривая левую и правую части равенства как подынтегральные выражения, получаем
![]() (5.5.1)
(5.5.1)
Произвольная постоянная в правой части равенства не пишется (почему?).
Формула (5.5.1)
выражает метод интегрирования по
частям. Этот метод уместно использовать
в тех случаях, когда функция u(x)
при дифференцировании упрощается.
Поэтому в качестве u(x)
выбирают функции
![]() и
т.п.
и
т.п.
П р и м е р. Вычислить интеграл
![]()
Решение выглядит следующим образом:
![]() =
=![]()
![]()
=![]()
Следует обратить внимание на то, как усложняется вид функции при действии на неё оператора интегрирования. Это явление является типичным.
Задание для самостоятельного решения.
Интегрированием по частям найти следующие интегралы:
1)
![]() 2)
2)
![]() 3)
3)
![]()
4)
![]() 5)
5)
![]() 6)
6)
![]()
Как вычислить интегралы вида:
![]()
![]()
![]()
если
степень многочлена
![]() выше
единицы?
выше
единицы?
5. 6. Понятие определенного интеграла как предела интегральной суммы.
Пусть
![]() и поставлена известная из школьного
курса задача о вычислении площади
криволинейной трапеции (рис. 5.2).
и поставлена известная из школьного
курса задача о вычислении площади
криволинейной трапеции (рис. 5.2).

y=f(x)








О
а b x
y
Разобьем отрезок
![]() на n частей (не
обязательно равных по длине). Абсциссы
границ полученных частей обозначим
через
на n частей (не
обязательно равных по длине). Абсциссы
границ полученных частей обозначим
через
![]() (рис. 5.3). Выберем, далее, точки
(рис. 5.3). Выберем, далее, точки
![]() где
где
![]() ,
и образуем выражение
,
и образуем выражение
![]() (5.6.1)
(5.6.1)
З
у= f(x)
![]() - длина i – ой части
отрезка
.
- длина i – ой части
отрезка
.
y
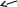








x
0

![]()
![]()
![]()
![]()
![]()
Рис. 5.3
Величина
![]() называется интегральной суммой.
Очевидно, что
выражает площадь ступенчатой фигуры
(рис. 5.3), которая заштрихована.
называется интегральной суммой.
Очевидно, что
выражает площадь ступенчатой фигуры
(рис. 5.3), которая заштрихована.
Если выбрать точки
![]() так, что
так, что
![]()
ступенчатая фигура окажется вложенной в криволинейную трапецию. Если же, наоборот, подобрать таким образом, чтобы
![]()
то криволинейная трапеция окажется вложенной в такую ступенчатую фигуру.
При
![]() разности
разности
![]() тоже стремятся к нулю, и интуитивно
ясно, что величина
тоже стремятся к нулю, и интуитивно
ясно, что величина
![]() независимо от того, как x
независимо от того, как x
производится разбиение отрезка на части и каким образом выбираются точки для каждой из этих частей. Величина
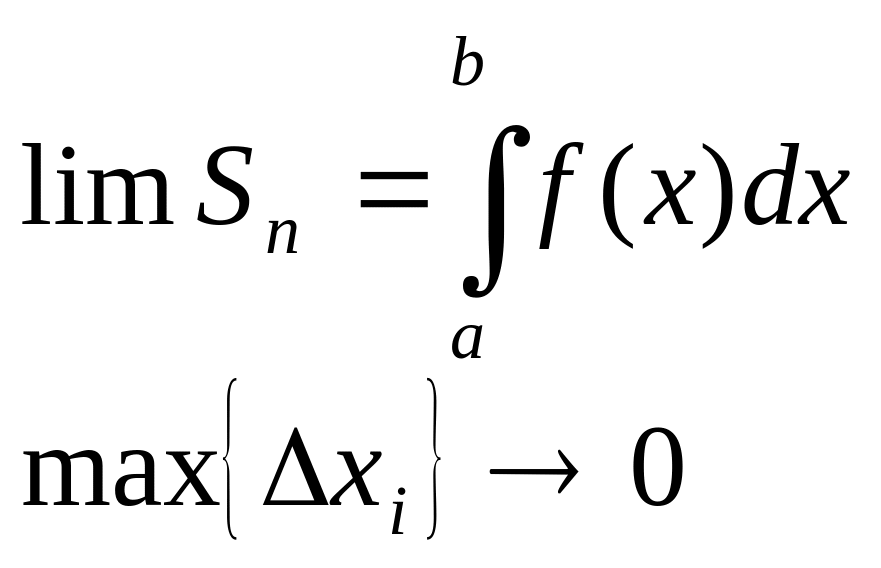 (5.6.2)
(5.6.2)
называется определённым интегралом от функции f(x) по отрезку , а –называется нижним пределом интегрирования, b – верхним пределом интегрирования.
В формуле (5.6.2) понятие предела уточнить, так как зависит от переменного количества аргументов:
![]()
Делается это следующим образом:
![]()
Определенный
интеграл отображает функцию
![]() на число
на число
![]() т.е. является функционалом из С в
R.
т.е. является функционалом из С в
R.
Если
![]() то величину определенного интеграла
естественно принять за площадь
криволинейной трапеции
то величину определенного интеграла
естественно принять за площадь
криволинейной трапеции
![]() ,
так как
,
так как
![]()
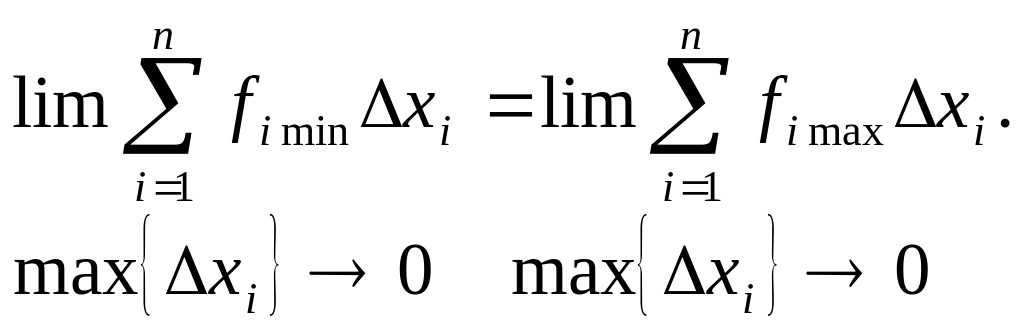
Можно доказать, что если , то определенный интеграл (5.6.2) существует.
Задание для самостоятельного решения.
Запишите выражение площади полукруга радиуса r с центром в начале координат в виде определенного интегралаю
Приведите примеры из физики, химии, механики, когда приходится рассматривать определенный интеграл.
Подумайте, существует ли определенный интеграл от функции Дирихле
![]()
