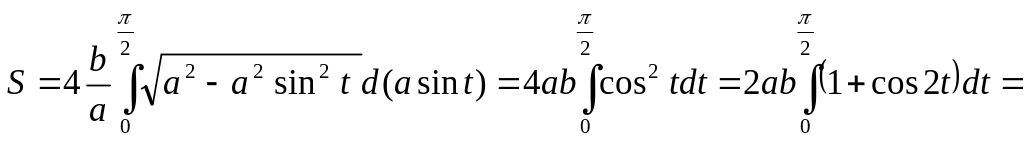- •Глава пятая. Интегральное исчисление для числовой функции одной переменной.
- •Первообразная и неопределенный интеграл.
- •5.2.Основные свойства неопределённого интеграла.
- •Интегрирование подстановкой.
- •5.5. Интегрирование по частям.
- •5. 6. Понятие определенного интеграла как предела интегральной суммы.
- •5.7. Формула Ньютона-Лейбница.
- •5.8. Основные свойства определённого интеграла.
- •5.9. Оценки определенного интеграла.
- •5.10. Теорема о среднем значении.
- •5.11. Вычисление определённых интегралов с помощью подстановки.
- •5.12. Вычисление определённых интегралов путём интегрирования по частям.
- •5.13. Практическая схема применения определенных интегралов для решения прикладных задач.
- •5.13.1. Вычисление площадей плоских областей.
- •5.13.2. Вычисление длины дуги плоской кривой.
- •5.13.3. Вычисление объёма и площади поверхности тела вращения.
- •5.13.4 Вычисление объёма тела с заданными площадями параллельных сечений.
- •5.14. Примеры физических приложений определённых интегралов.
- •5.15. Приближениое вычисление определённых интегралов.
- •5.15.1. Формула прямоугольников.
- •5.15.2. Формула трапеций.
- •5.15.3. Формула парабол.
- •5.16. Несобственные интегралы.
- •5.16.1. Несобственные интегралы с бесконечными пределами интегрирования
- •5.16.2 Несобственные интегралы от разрывных функций.
- •5.16.3. Теоремы о сходимости несобственных интегралов
- •Интеграл как функция пределов интегрирования. Понятие о специальных функциях, определяемых интегралами с переменным верхним пределом.
- •5.18. Понятие об интегралах, зависящих от параметра
- •5.19. Понятие о гамма-функции
- •Комплексные числа.
- •5.1. Основные понятия о комплексных числах.
- •5.2. Запись комплексных чисел в тригонометрической и
- •5.3. Разложение многочлена на множители в случае действительных и мнимых корней.
- •5.4. Разложение правильной рациональной дроби на простейшие дроби
- •Глава шестая. Кратные, криволинейные и поверхностные интегралы; элементы теории поля.
- •Понятие об интеграле по замкнутой ограниченной области
5.9. Оценки определенного интеграла.
Рассмотрим свойства определенных интегралов, которые выражаются неравенствами и могут служить для оценки значений этих интегралов.
Теорема 1 (интегрирование неотрицательной функции):
![]()
Доказательство:
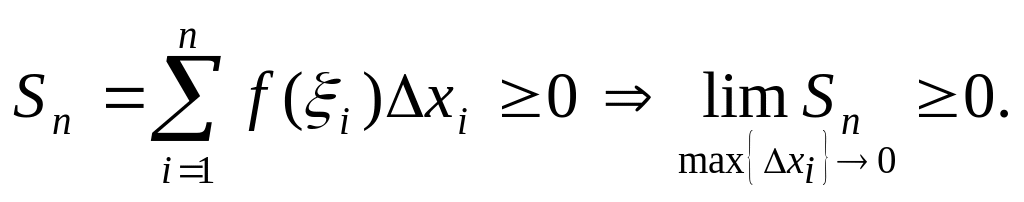
Теорема 2 (интегрирование неравенств):
![]()
Доказательство:
![]()
Теоремы
1 и 2 показывают, что неравенства можно
интегрировать (a![]()
Теорема 3 (двойная оценка определенного интеграла):
![]() (5.9.1)
(5.9.1)
Доказательство основано на возможности интегрирования неравенств:
![]()
C![]()
y![]()
y=f(x)


B
A
![]()
x
a
b
O
Рис. 5.4
Неравенства (5.9.1) дают двойную оценку определенного интеграла:снизу и сверху.
Теорема 4 (оценка модуля определенного интеграла):
![]() (5.9.2)
(5.9.2)
Доказательство:
![]() Неравенство
(5.9.2) напоминает известное свойство
модуля суммы нескольких чисел:
Неравенство
(5.9.2) напоминает известное свойство
модуля суммы нескольких чисел:
![]()
Если
![]() ,
то из (5.9.2) получаем ещё одну оценку
модуля определенного интеграла:
,
то из (5.9.2) получаем ещё одну оценку
модуля определенного интеграла:
![]() (5.9.3)
(5.9.3)
Неравенства (5.9.1), (5.9.2), (5.9.3) используются при доказательстве различных теорем, а также для грубой оценки значения определенного интеграла.
5.10. Теорема о среднем значении.
Введём понятие о среднем
значении функции
![]() Для этого разобьём отрезок
Для этого разобьём отрезок
![]() на n частей
одинаковой длины
на n частей
одинаковой длины
![]() Далее выберем точки
Далее выберем точки
![]() и введём соответствующие им значения
функции
и введём соответствующие им значения
функции
![]() Тогда
в качестве среднего значения функции
Тогда
в качестве среднего значения функции
![]() на
естественно принять величину
на
естественно принять величину
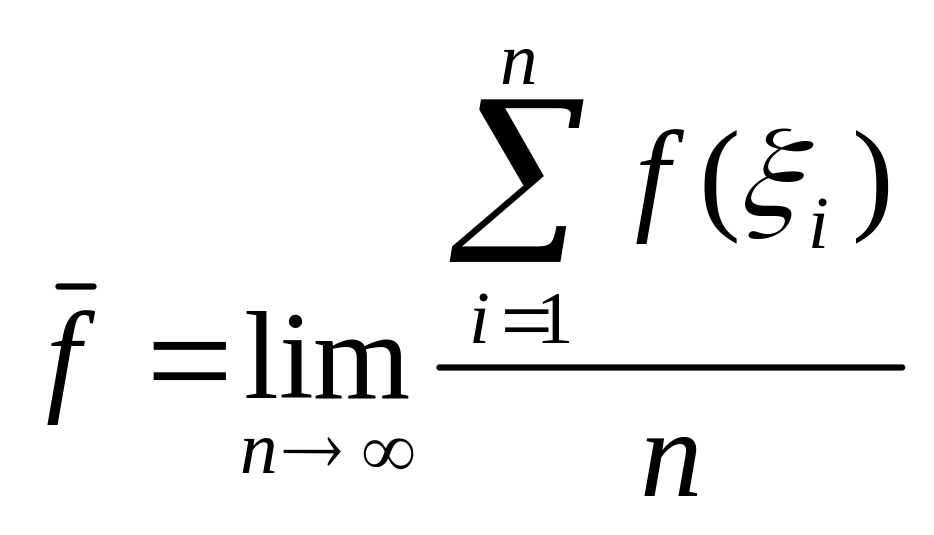 или
или
 т.е.
т.е.
![]() (5.10.1)
(5.10.1)
Величину
![]() называют ещё средним интегральным
значением функции
на
.
называют ещё средним интегральным
значением функции
на
.
Теорема (о
среднем значении). Если
![]() С
,
то существует такая точка
С
,
то существует такая точка
![]() ,
в которой
,
в которой
![]() =
.
=
.
Для доказательства воспользуемся двойным неравенством (5.9.1), записав его в виде
![]()
откуда в силу (5.10.1)
![]()
Если в качестве
m и M
выбрать наименьшее и наибольшее
значение функции
на
,
то в силу теоремы Вейерштрасса существует
точка
![]() ,
в которой
=
(число
расположено между m
и M, а непрерывная
функция “не пропускает” ни одного
значения между m и M
).
,
в которой
=
(число
расположено между m
и M, а непрерывная
функция “не пропускает” ни одного
значения между m и M
).
Геометрический
смысл теоремы о среднем значении состоит
в том, что существует точка
,
в которой
![]() или
в соответствии с обозначениями рис. 5.6
или
в соответствии с обозначениями рис. 5.6
![]()
A
B
D

C

y
x
0
a
b
ξ
Рис. 5.6
5.11. Вычисление определённых интегралов с помощью подстановки.
Теорема. Если
С
,
![]() причём функция
причём функция
![]() отображает
отрезок
отображает
отрезок
![]() на
отрезок
,
на
отрезок
,
![]()
![]() то
то
![]() (5.11.1)
(5.11.1)
Доказательство:
![]()
![]()
(здесь
![]()
При вычислении определённого интеграла с помощью подстановки возвращаться к прежней переменной интегрирования не нужно. Однако не следует забывать о необходимости изменения пределов интегрирования.
П р и м е р: Вычислить площадь эллипса
![]()
Очевидно, что искомая площадь
![]()
С помощью подстановки
![]()
![]()
![]()
п![]() олучаем
олучаем