5.18. Понятие об интегралах, зависящих от параметра
Рассмотрим интеграл
(5.18.1)
Здесь величина
х при интегрировании постоянна, но
её значение можно выбирать по-разному,
т.е. х является параметром. Очевидно,
что в случае непрерывной по t
функции
формула (5.18.1) определяет некоторую
функцию
при
Таким
образом, функцию
считаем определенной в прямоугольнике
Количество параметров может быть и большим. Например,
Интегралы, зависящие от параметров, обладают следующими свойствами (приводятся без доказательства):
если функция
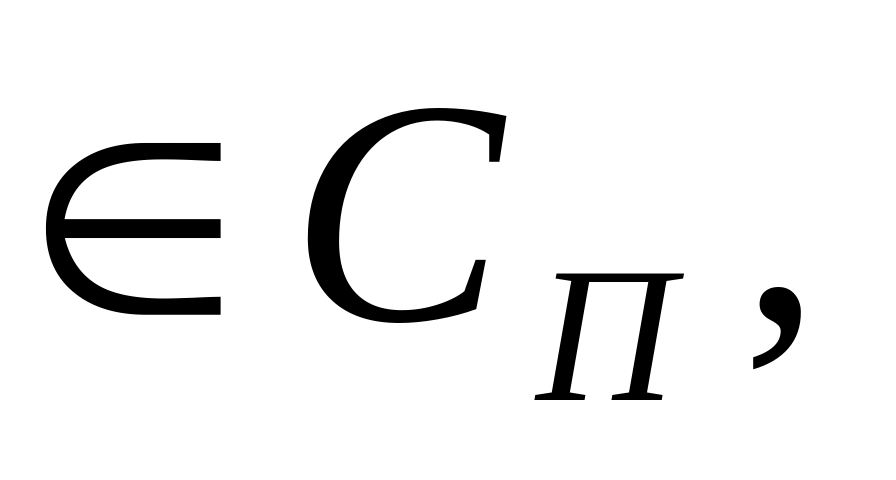то интеграл (5.18.1) определяет функцию
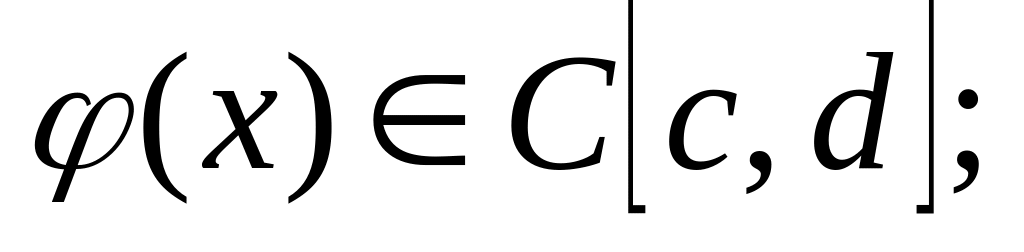
если частная производная
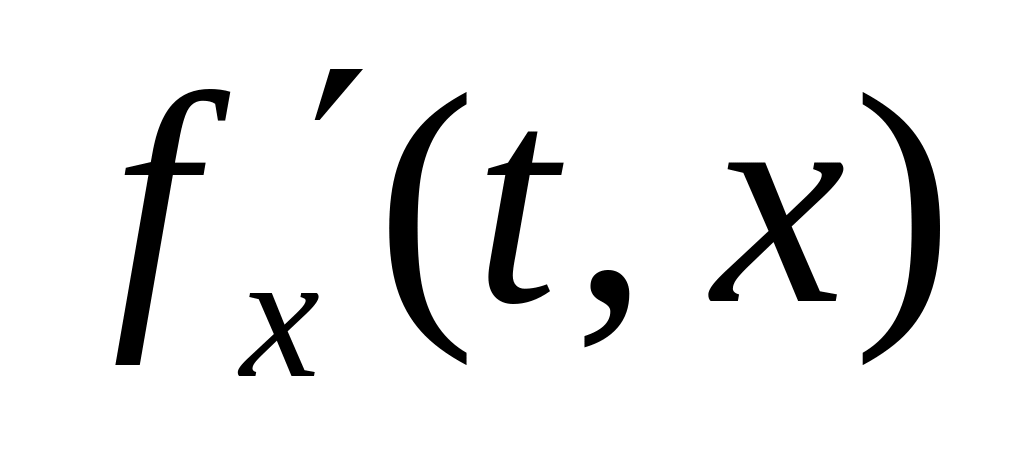то возможно дифференцирование по
параметру под знаком интеграла (правило
Лейбница), т.е.
(5.18.2)
если то возможно интегрирование по параметру под знаком интеграла:
(5.18.3)
Выведем формулу дифференцирования по параметру, когда верхний предел интегрирования зависит от этого параметра:
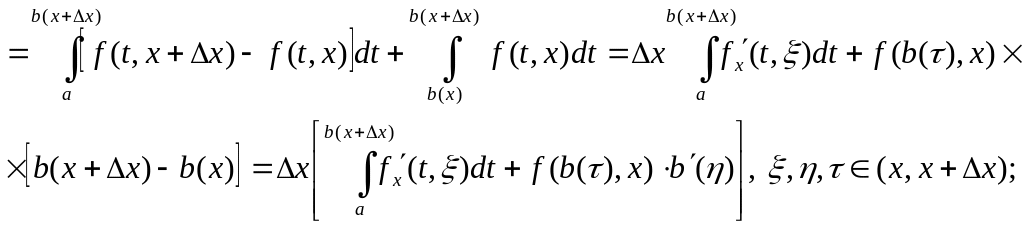
Окончательно имеем:
П р и м е р:
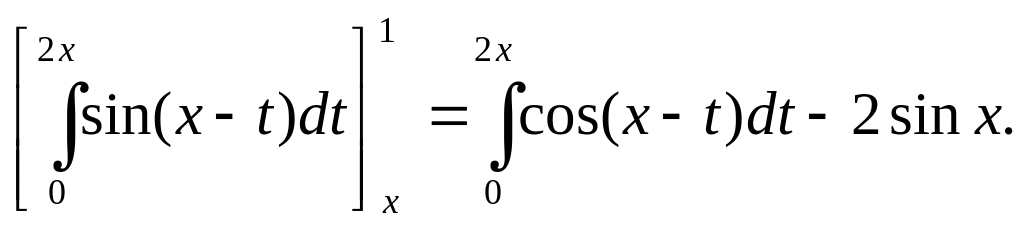
Несобственные интегралы, зависящие от параметра, ведут себя несколько сложнее.
Рассмотрим, например, интеграл
(5.18.4.)
где определена и непрерывна на полуполосе
Если
то
этого условия оказывается недостаточно
для того, чтобы
В связи с этим вводится условие правильной
(равномерной) сходимости интеграла
(5.18.4): должна существовать такая функция
что
Оказывается, что добавив
условие правильной сходимости, можно
распространить указанные выше свойства
на случай несобственных интегралов,
зависящих от параметра (свойства 1 и 3
верны при правильной сходимости интеграла
(5.18.4), Свойство 2 справедливо, если
правильно сходится интеграл (5.18.2) при
5.19. Понятие о гамма-функции
Рассмотрим интеграл, определяющий гамма-функцию (Г-функция, или Эйлеров интеграл второго рода):
(5.19.1)
Этот интеграл зависит от параметра и является несобственным (с бесконечным верхним пределом). Кроме того, если х<1, он имеет особенность при t=0.
Сходимость интеграла (5.19.1) как несобственного с бесконечным верхним пределом имеет место при любом х, так как при достаточно больших значениях t
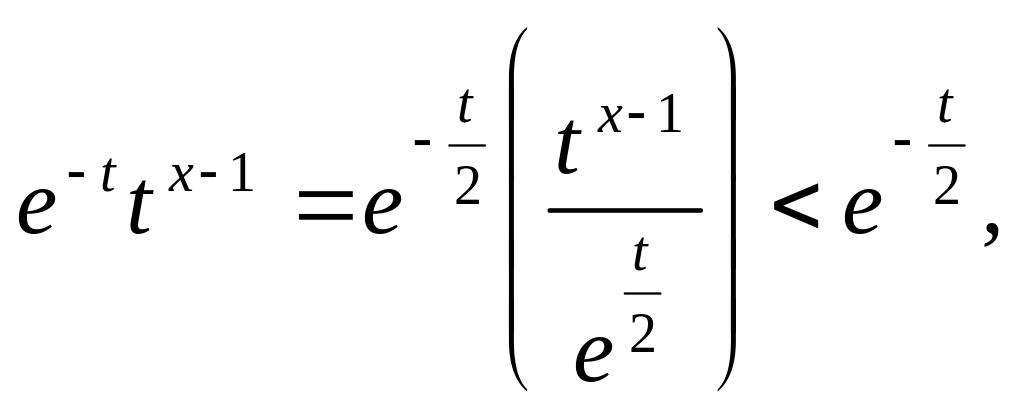
поскольку
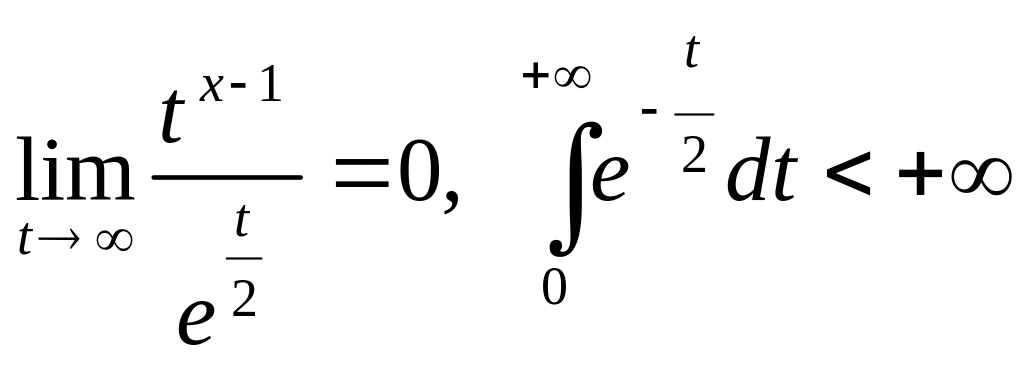
(предел вычисляется с помощью правила Лопиталя).
Рассмотрим теперь сходимость
интеграла (5.19.1) как несобственного
интеграла от разрывной функции при
Поскольку
будем иметь сходящийся интеграл
при
т.е. при
При
интеграл расходится, так как для любого
существует такое
что
при
имеет место неравенство
т.е.
и
Таким образом, формула (5.19.1) имеет смысл при всех
Установим теперь основное свойство гамма-функции:
т.е.
(5.19.2)
Вычислим
Тогда, положив в (5.18.6)
получим
т.е. гамма-функция является интерполирующей для факториала
(5.19.3)
С помощью формулы (5.18.7) можно определить 0!: эту величину естественно считать равной единице. Далее, используя формулу (5.19.2) как определяющую, имеем
(5.19.4)
при любых х. Поэтому можно
продолжить
для
затем для
и т.д. В результате получается функция,
определенная всюду в R,
кроме точек х=0, -1, -2, … и, как следует
из (5.19.3), (5.19.4) бесконечно возрастающая
при
(рис. 5.22).
Рис. 5.22
Приложение