5.12. Вычисление определённых интегралов путём интегрирования по частям.

Формула интегрирования по частям для определённого интеграла выводится очень просто

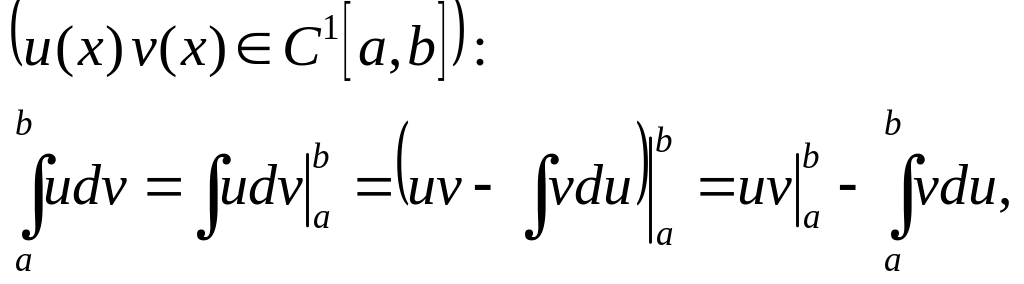
т.е.

(5.12.1)

П р и м е р:

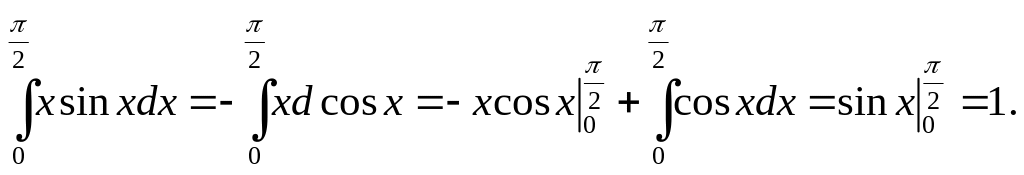
Задание для самостоятельного решения.

1. Найдите средние значения функций:

а) на отрезке

б) на отрезке и

2. Сила переменного тока изменяется по закону

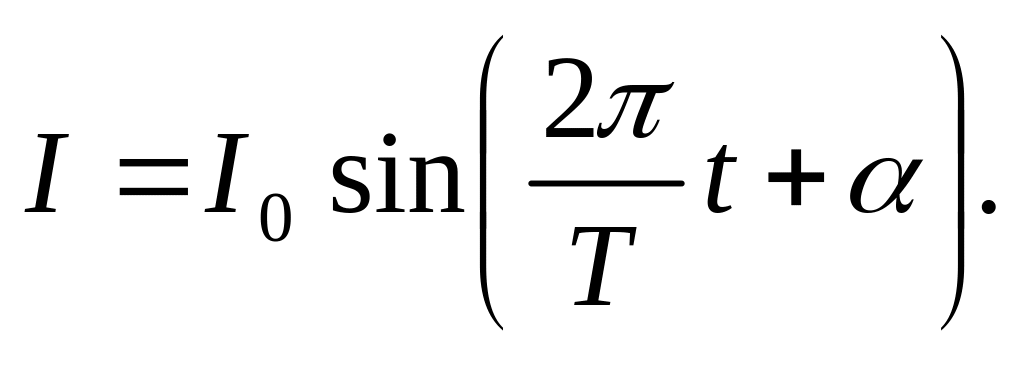
Найдите среднее значение силы тока за полупериод.

3. Оцените интегралы:

а) б)

4. Подумайте, можно ли вычислить определённые интегралы с помощью указанных подстановок:

а)

б)

5. Покажите справедливость приводимого ниже рекуррентного соотношения путем интегрирования по частям:

если

Вычислите

5.13. Практическая схема применения определенных интегралов для решения прикладных задач.

Пусть некоторая величина Q распределена вдоль отрезка , причем Q(x) выражает значение Q на отрезке Тогда для Q можно ввести понятие линейной плотности:

где - количество рассматриваемой величины на отрезке длиной

Имеем

т.е.

(5.13.1)

Произведя стандартное разбиение отрезка на n частей, будем иметь равенство (5.13.1) для n точек

откуда следует, что

Обозначив

получим

т.е.

(5.13.2)

Таким образом, из равенства (5.13.1) следует (5.13.2), и мы получили широко используемое правило применения определенных интегралов:для вычисле-ния величины распределенной вдоль отрезка с линейной плотностью достаточно воспользоваться импликацией:

(5.13.3)

При использовании формулы (5.13.3) плотность на элементарном отрезке длиной dx можно считать постоянной (она совпадает с где

5.13.1. Вычисление площадей плоских областей.

1. Если кривые, ограничивающие область, заданы обычными уравнениями в декартовых координатах (рис. 5.7), то площадь S области вычисляем с помощью (5.13.3):

Короче это записывают так: (5.13.4)

п

d S

y

олагая, что

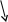
S

x

0

a

b

d x

Рис. 5.7

2. Если кривая задана в декартовых координатах параметрическими уравнениями, то площадь соответствующей криволинейной трапеции вычисляется с помощью замены переменной интегрирования

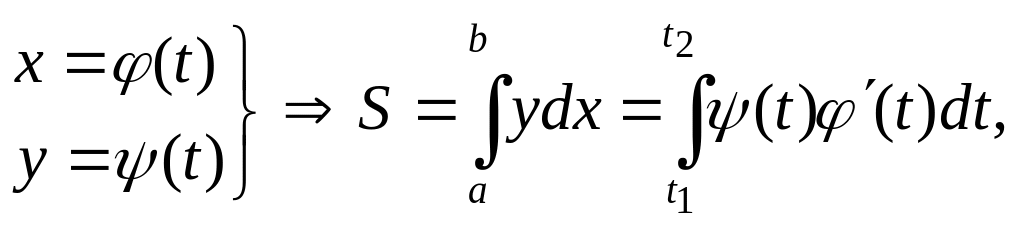
где либо известны из формулировки задачи, либо их находят из уравнений

3. Пусть теперь кривая задана в полярных координатах уравнением , требуется вычислить площадь сектора, показанного на рис. 5.8

S

ρ=f(φ)

dS

β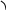

α

Рис. 5.8

Поскольку элементарный сектор аппроксимируется круговым, то

Отсюда согласно (5.13.3)

или, короче,

(5.13.5)

П р и м е р: Найти площадь, ограниченную лемнискатой Бернулли (рис. 5.9).

Данная кривая имеет две симметричные относительно полюса ветви Поэтому достаточно рассмотреть лишь одну ветвь Нетрудно видеть, что

и вся ветвь расположена в секторе (рис. 5.9). Поэтому согласно (5.13.5)

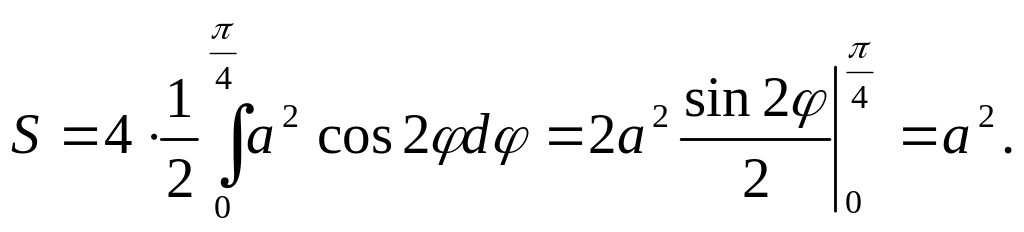
0

N

a

Рис. 5.9

Задание для самостоятельного решения.

1. Подумайте, как вычислить площадь криволинейной трапеции, ограниченной прямыми 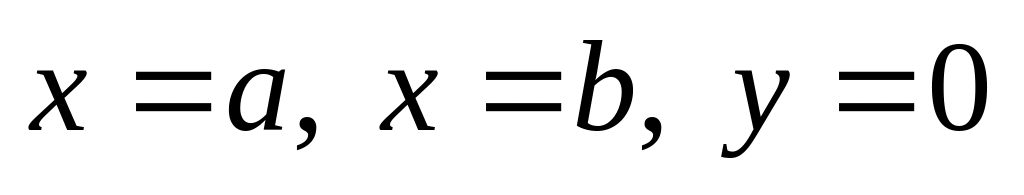и кривой 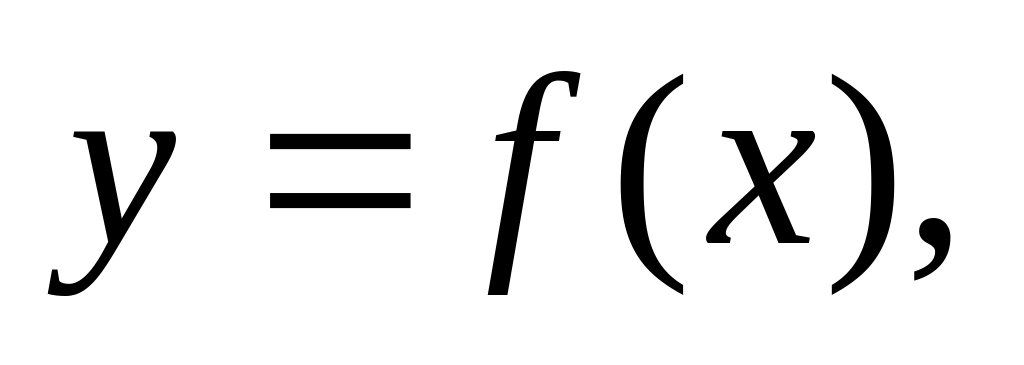если f(x) на отрезке изменяет знак.

2. Найдите площади фигур, ограниченных линиями:

а)

б)

в)

3. Найдите площади фигур, ограниченных линиями:

а) кардиоидой

б) окружностями

в) первым витком спирали Архимеда и полярной осью;

г) трехлепестковой розой

Сделайте чертежи.

4. Вычислите площади фигур, ограниченных

а) эллипсом

б) астроидой

в) первой аркой циклоиды и осью ОХ.