5.16.1. Несобственные интегралы с бесконечными пределами интегрирования
Пусть
т.е. функция f(x)
непрерывна на отрезке
при любом b>a.
Интеграл
(5.16.1)
называется несобственным интегралом.
Говорят, что несобственный интеграл сходится, если существует конечный предел (5.16.1). Если не существует конечного предела (5.16.1), то несобственный интеграл называют расходящимся.
С геометрической
точки зрения величина (5.16.1) выражает
площадь бесконечной фигуры, ограниченной
кривой
осью
абсцисс и прямой x=a
(рис. 5.19).
y
y=f(x)
0
x
a
b
Рис. 5.19
Аналогично вводятся и другие несобственные интегралы с бесконечными пределами интегрирования:
где
выбирается произвольно (докажите
самостоятельно, что от выбора с значение
интеграла не зависит). Для последнего
сходимость определяется сходимостью
обоих интегралов в правой части равенства.
П р и м е р:
Рассмотренные несобственные интегралы называют иногда несобственными интегралами первого рода.
5.16.2 Несобственные интегралы от разрывных функций.
Пусть
,
а в точке x=b
она имеет разрыв второго рода. Тогда
интеграл
(5.16.3)
называется несобственным интегралом (сходящимся, если предел (5.16.3) существует и конечен; расходящимся – в остальных случаях. Несобственные интегралы от разрывных функций называют ещё несобственными интегралами второго рода.
Геометрический смысл несобственного интеграла ясен из рис. 5.20.
y
y=f(x)
0
x
a
b
b-E
Рис. 5.20
Аналогично
вводятся несобственные интегралы в
случаях, когда подынтегральная функция
имеет иначе расположенную точку разрыва.
Так, если f(x)
имеет разрыв при x=a,
т.е.
то
(5.16.4)
Если точка разрыва x=с лежит между точками x=a и x=b, то
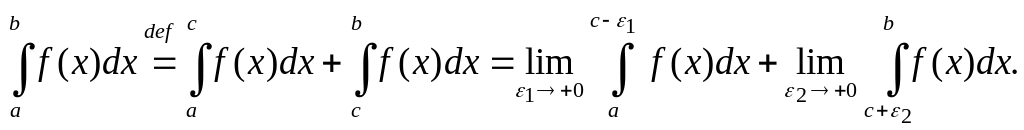(5.16.5)
В качестве упражнения вычислим интеграл
Поскольку
подынтегральная функция имеет разрыв
в точке
,
то, учитывая (5.16.5) имеем:
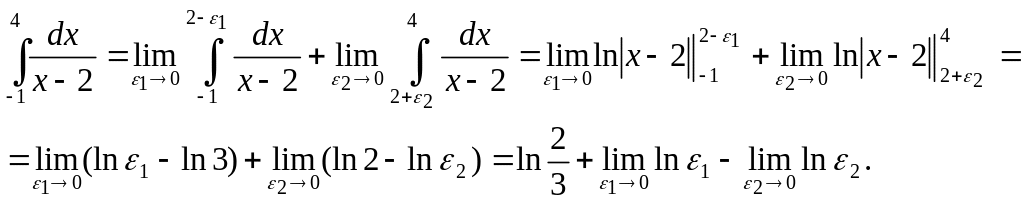
Очевидно, что интеграл расходится.
Если на отрезке функция f(x) имеет несколько точек разрыва, то несобственный интеграл определяется аналогично.
В некоторых
задачах вместо (5.16.4) целесообразно
ввести понятие главного значения
несобственного интеграла.
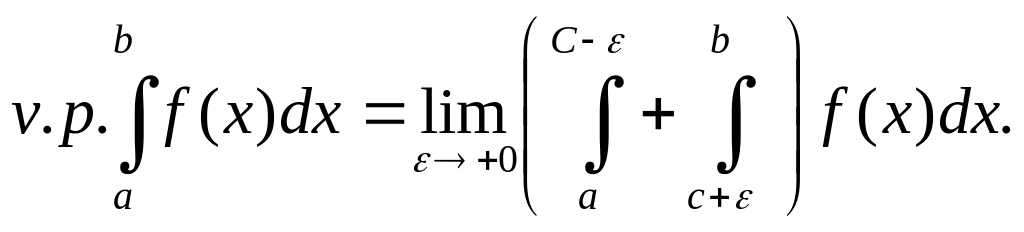(5.16.6)
Здесь точка
разрыва «вырезана» из отрезка
вместе с симметричным относительно нее
промежутком
Поэтому, если сходится интеграл (5.16.5),
то сходится и (5.16.6). Обратное же утверждение
неверно: (5.16.6) может сходиться, а (5.16.5) –
расходиться.
Например, интеграл, рассмотренный в предыдущем упражнении расходится, хотя существует в смысле главного значения (убедитесь в этом самостоятельно).
Заметим, что в случае, когда функция f(x) имеет разрыв первого рода, нет принципиальной необходимости вводить понятие несобственного интеграла: достаточно разбить отрезок на два отрезка, доопределив на каждом из них f(x) по непрерывности (рис. 5.21) и рассмотрев два обычных интеграла.
y
0
x
a
c
b
Рис. 5.21
Основные свойства несобственных интегралов аналогичны свойствам определённых интегралов и легко получаются из них предельным переходом с учётом определений (5.16.1) – (5.16.5).
Задание для самостоятельного решения.
Подумайте, как связано существование несобственного интеграла (5.16.1) с существованием конечного предела.
Вычислите несобственные интегралы первого рода:
1)
2)
3)
4)
Вычислите несобственные интегралы второго рода:
1)
2)
3)
4)
Подумайте, как ввести
Чему будет равно
если f(x) – нечётная функция?
Вычислите:
1)
2)
3)
4)
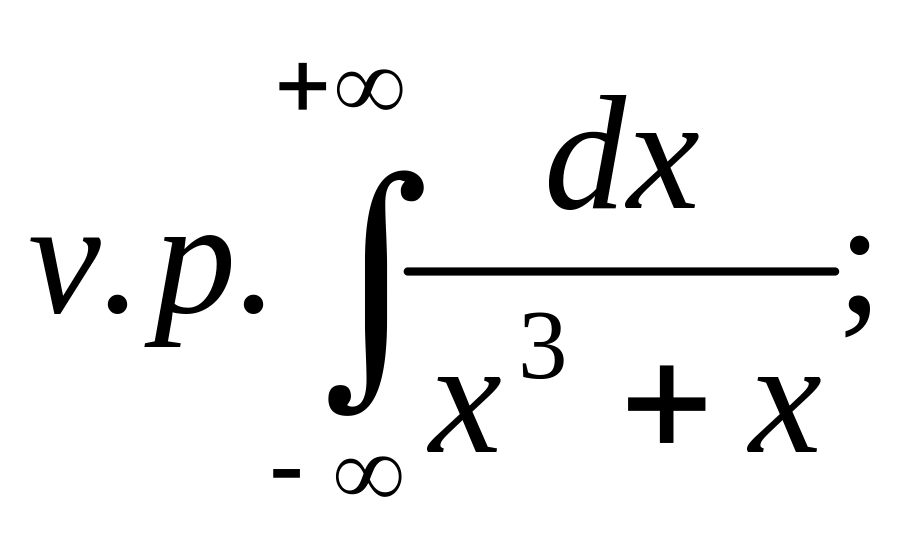5)
