150

11. Информационные модели сигналов

11.1 Количество информации и информационная емкость сигнала

Рассмотренные модели описывают сигналы как физические процессы. Они созданы для исследования взаимодействия сигналов с различными техническими устройствами. Но важная, если не важнейшая роль сигналов в том, что они переносят сообщения. Поэтому необходимы способы описания, исследования и синтеза сигналов как переносчиков информации.

Способы измерения такого сложного феномена, как информация, очень сильно различаются для разных предметных областей. Информационная емкость библиотек измеряется количеством томов, полиграфисты измеряют информацию печатными листами. На радио и телевидении информацию измеряют минутами "Эфирного времени". Наиболее конструктивна и традиционна мера, используемая в теории и технике передачи информации. Это количество информации"по Шеннону". Оно связано с условием выбора конкретного сообщенияs(или сигнала, переносящего это сообщение) из ансамбляsS:

,

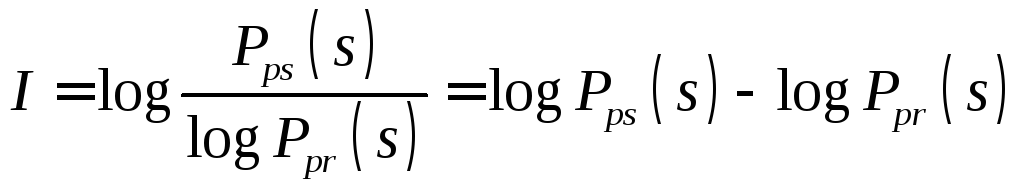где Р_pr(s) - априорная вероятность сообщенияs, а

Р_ps(s) - апостериорная вероятность того, что принятый сигнал содержит именно сообщениеs.

Если сообщение при передаче не искажено, Р_ps(s)1 иI=-log Р_pr(s).

Источник информации может формировать разные сообщения. У разных сообщений могут отличаться априорные вероятности. Поэтому кроме величины количества информации Iрассматривается среднее количество информации на одно сообщение, которое может быть сформировано источником:

,

где К- полный объем ансамбля сообщенийs_k, которые может формировать источник.

Как видно энтропия - это математическое ожидание величины logР_pr(s). Чем больше энтропия источника, тем больше, в среднем, степень априорной неопределенности формируемого им сообщения.

После приема сообщения неопределенность уменьшается (во всяком случае - не увеличивается). Поэтому количество информации может трактоваться как мера уменьшения неопределенности.

Энтропия, как видно из (2.2), неотрицательна, но равна нулю только для вырожденного ансамбля, содержащего всего одно сообщение, такое, что Р_ps(s_i)=1,Р_ps(s_j)=0;ij;i,j1:K.

Энтропия аддитивна: для совокупности источников энтропия равна сумме энтропий каждого:

.

Из видно, что энтропия имеет ту же размерность, что и количество информации. Эта размерность зависит от выбора основания логарифма в и . Если логарифм берется по основанию 2, как чаще всего и бывает, информация и энтропия измеряются в двоичных единицах, или битах (BInarydigiT). Один бит это количество информации, содержащееся в неискаженном при передаче сообщенииР_ps=1, которое априори может принимать два равновероятных значенияР_pr(s₀)=Р_pr(s₁)=. Действительно, из :. Кратные одному биту величины количества информации – 1 байт=2³=8 бит, 1 Кбайт=2¹⁰байт=2¹³бит и т.д.

Объем запоминающего устройства (ЗУ) в 1 Мбайт означает, что оно (ЗУ) может быть источником, содержащим сообщения общим суммарным количеством информации до 2^20.2³бит, или, что то же самое, может запоминать информационные массивы объемом 2^20.2³бит. Разумеется, это верхнее, потенциальное значение. Если ЗУ не заполнено (или заполнено данными, не содержащими информации) энтропия такого источника будет меньше.

Другая важная для оценки информативности сообщений величина - взаимная информация. Это информация, которую содержит один ансамбль сообщений (или сигналов) относительно другого. Например - ансамбль принятых сообщений относительно ансамбля сообщений переданных. Или массив шифровок относительно породившего его ансамбля открытых сообщений.

Пусть имеется два ансамбля Аи В дискретных сообщенийа_kАиb_lВ. Совместная вероятность сообщенийа_kиb_l - это Р(а_k,b_l). А совместная энтропия ансамблейАиВбудет, по определению, математическим ожиданием логарифма совместного распределения:

.

Для условного распределения аналогичным образом можно определить условную энтропию:

.

Используя теорему Байеса

,

для можно установить, что

.

Нетрудно также установить, что

.

Равенство Р(А|В)=0 выполняется тогда, когда ансамбльВсодержит всю информацию об ансамблеА. В другом крайнем случаеозначает, что ансамблиАиВсодержат независимые сообщения, т.е.В не содержит информации обА.

Поскольку, как видно из , условная энтропия Н(А|В) никогда не бывает большеН(А), можно утверждать, что знаниеВуменьшает (в среднем) априорную неопределенность относительноА. Неопределенность уменьшается за счет приобретения информации. Поэтому разность

называется количеством взаимной информации в ансамбле ВотносительноА.

Используя определения энтропии , и нетрудно показать, что

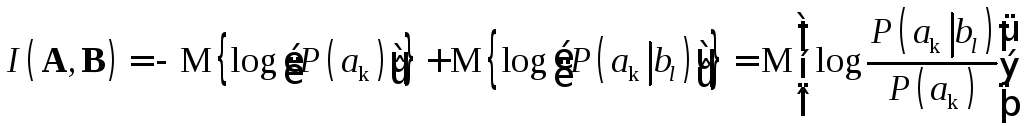
Если Р(а_k|b_l) - условная вероятность передачи символаа_kпри условии, что принят символb_l, аР(а_k) - априорная вероятность событияа_kАто,I(A,B) показывает, сколько в среднем информации передается по каналу, воспроизводящему на выходе сообщение из ансамбляВ.

Обозначив величиной Тсреднее время передачи одного сообщения, можно оценить скорость передачи информации отАкВ:

.

С такой скоростью сообщения передаются по информационному каналу, будь то канал передачи или утечки информации. Эта скорость зависит как от свойств источника информации, так и от свойств самого канала. Максимально достижимая скорость при заданном качестве передаваемой информации с=max R(A,B) называется пропускной способностью канала передачи и является важнейшей характеристикой информационной системы. Для оценки пропускной способности можно привести следующие рассуждения.

Пусть по дискретному каналу передаются сигналы, содержащие по nсимволов каждый, и пусть эти символы выбираются из алфавита, который содержитmсимволов (имеет объемm). Каждый такой сигнал может приниматьNразных значений и, соответственно, переносить информацию обNразных сообщениях. Естественно,

при	n=1	N=m,
при	n=2	N=m^2,
………………………………………….
при	n	N=m^n,

Если все сигналы в информационной системе независимы (канал без памяти), равновероятны и принимаются без искажений (Р_ps=1), а длительность передачи каждого сигналаT=n_cравна сумме длительностей передачи элементов, из которых он состоит, (символов), то скорость передачи информации составит:

.

Для передачи символа (элементарного сигнала) длительностью _cканал передачи данных должен иметь ширину полосы пропускания. Именно такую полосу частот занимает сигнал, длительностью_c. Поэтому для дискретного канала без памяти соотношение позволяет утверждать, что

.

Если условие неискаженной передачи не выполняется и в канале происходят ошибки с вероятностью Р, то апостериорная вероятность при приеме каждого символа будет равна уже не единице, а

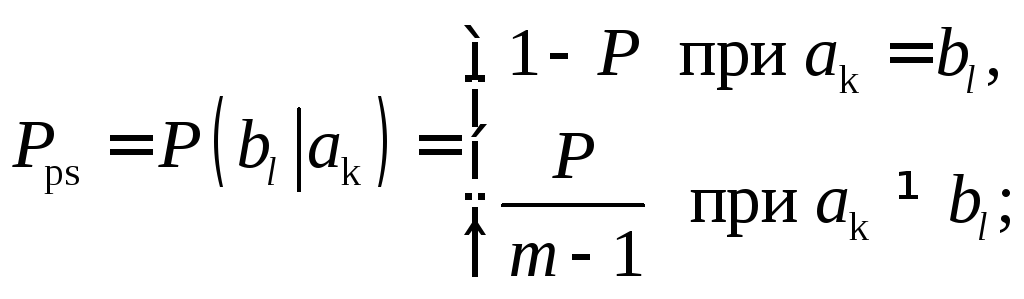
и входящая в величина количества информации должна определяться согласно , с учетом того, что Н(А) - энтропия источника сообщений - не зависит от свойств канала, а условная энтропия

.

Используя , и можно получить:

.

Для важного частного случая двоичного симметричного канала, когда m=2, а искажения противоположных по значению символов при передаче равновероятны, что иллюстрируется графом на рис. 11.1,

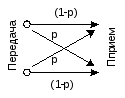
Рис.11.1. Граф изменений символов в двоичном симметричном канале

пропускная способность выражается соотношением

Зависимость удельной пропускной способности, нормированной к соотношению сигнал/шум в двоичном симметричном канале, от вероятности искажения символа представлена на рис.11.2

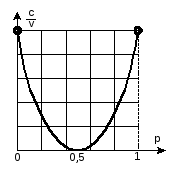
Рис.11.2. Нормированная пропускная способность двоичного симметричного информационного канала

Как видно из и графика рис.2.2, при Р=0,5 пропускная способность равнас=0. В содержательных терминах этот это означает, что при такой вероятности ошибки сообщение можно и не передавать. Получателю сообщения можно просто выбирать его с равной вероятностью из двух возможных. Иначе говоря,с=0 соответствует обрыву информационного канала или полному блокированию канала утечки информации.

Скорость передачи информации по каналу максимальна с=max не только приР=0, что вполне естественно, но и приР=1. ПриР=1 все символы при передаче меняются на противоположные, но такой зеркально отраженный сигнал содержит всю ту же информацию, что и исходный, не искаженный.

В обоих крайних экстремальных случаях Р=0 иР=1 максимум пропускной способности (измеренной в бодах, 1 бод=1 бит/с) не превосходит численного значения ширины полосы пропускания информационной системы (в герцах).

В отличие от дискретных сигналов, состоящих не из конечного набора символов, выбранных из ансамбля (алфавита) конечного размера, непрерывные сигналы s(t) могут принимать значения из континуального множестваs[S_min;S_max], гдеS_max-S_min- динамический диапазон сигнала; и существовать во всех точках временного континуумаt[0;T]. Формальное применение использованных выше рассуждений для оценки пропускной способности канала передачи непрерывных сообщений может привести к парадоксальным результатам. Действительно, непрерывный сигнал, как показано на рис.11.3, можно уподобить последовательности сколь угодно коротких импульсов (дискретных сигналов), сколь угодно мало отличающихся по амплитуде.

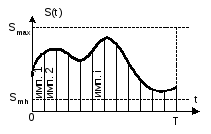
Рис.11.3. Представление непрерывного сигнала

Даже на конечном интервале времени существования непрерывного сигнала таких импульсов будет бесконечно много, и может показаться, что такая пачка импульсов содержит бесконечно большое количество информации. Кроме того, каждый из этих импульсов имеет амплитуду, равную соответствующему значению сигнала s(t), т.е. принимает значения на сегменте [S_min;S_max]. Если считать, что все множество импульсов различных амплитуд составляет алфавит, то придется признать объем этого алфавита бесконечно большим, а значит каждое сообщение, передаваемые символами такого алфавита, содержит бесконечно много информации. То есть, сведение непрерывного сигнала к пачке узких примыкающих друг к другу импульсов приводит к выводу о дурной бесконечности () в оценке пропускной способности информационного канала.

Противоречие между ограниченностью динамического диапазона сигнала конечной длительности и кажущейся бесконечностью его информационной емкости разрешается довольно просто. Если канал передачи (или утечки) информации имеет конечную ширину полосы пропускания w, а это условие совершенно естественно и выполняется для всех физически реализуемых систем, то сообщение на приемной стороне канала может быть совершенно точно восстановлено по своим дискретным значениям, следующим с периодом повторения. Это необходимое и достаточное положение обосновывается фундаментальной для теории и техники информационных систем теоремой В.А.Котельникова. Фактически условие точного восстановления сообщения означает, что выборка дискретных по времени значений сигнала, имеющая объем

содержит ту же информацию и в том же количестве, что и исходное непрерывное сообщение s(t).

Реально при передаче, приеме и обработке сигнала на него всегда накладываются помехи (шумы). Поэтому, передавая сигнал, бесполезно требовать представления его выборочных значений s[t=nt] с точностью, превосходящей уровень шумовых флуктуаций: чем больше средний уровень мощности шумаР_ш, сопровождающего прем сигнала мощностьюР_с, тем меньше разных значений сигнала можно различить на приеме рис.11.4.

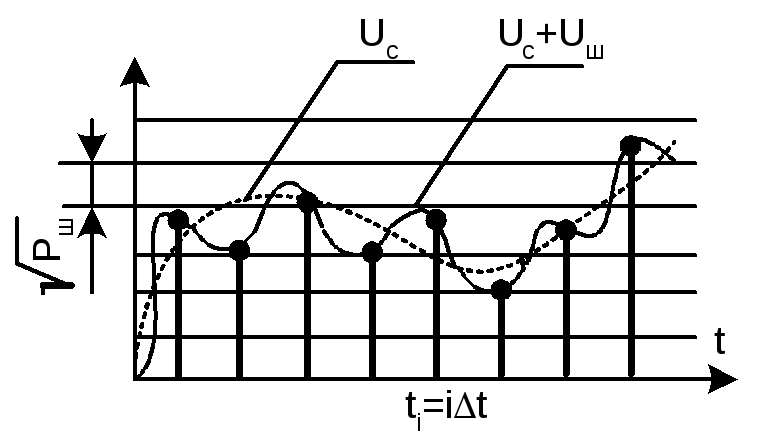
Рис.11.4. Конечное число различимых градаций сигнала, наблюдаемого на фоне шума

Иначе говоря, в условиях действия помех реально можно различать только mградаций уровня сигнала, причем

.

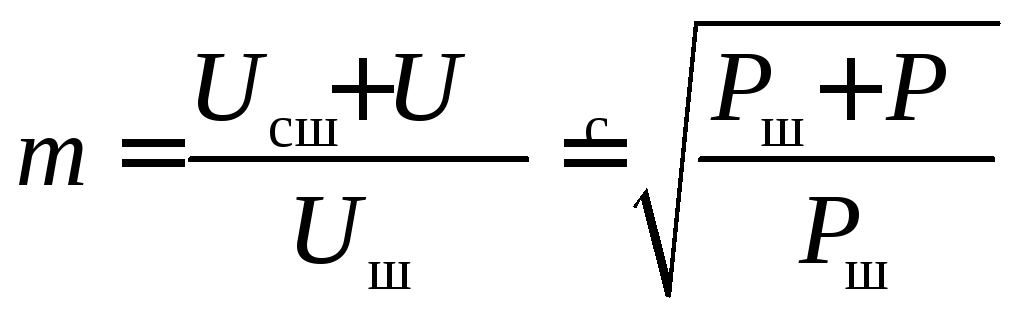Таким образом, непрерывный сигнал длительностью Ти шириной спектраwбудет содержать столько же информации, что и выборка изN=2wT+1 импульсов, способных принимать любое иззначений. Поэтому

,

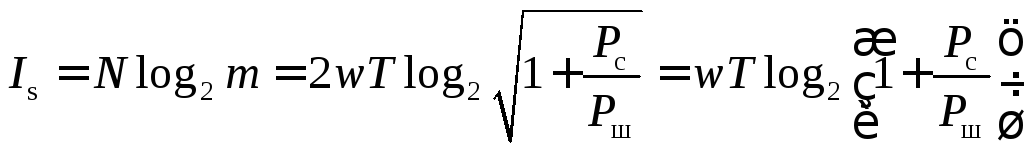а

.

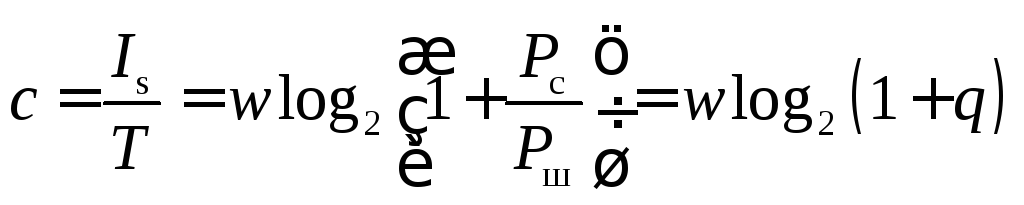Соотношение именуется формулой Шеннона. Оно универсально для любых информационных систем, вне зависимости от того, какие физические процессы и поля ими используются для образования каналов передачи, либо перехвата информации.

Из следует, что для увеличения пропускной способности информационного канала нужно либо увеличивать мощность сигнала (точнее - соотношение мощностей сигнала и шума ), либо расширять полосуw. Но эти способы неравноценны. С расширением полосыwпропускная способность растет линейно, а при измененияхqона меняется по логарифмическому закону, т.е. медленнее. Поэтому компенсировать сужение полосы спектра сигнала увеличением его мощности не всегда выгодно.

Если работе информационной системы противодействует нормальный стационарный шум со спектральной плотностью N₀, тоР_ш=wN₀и преобразуется к виду

.

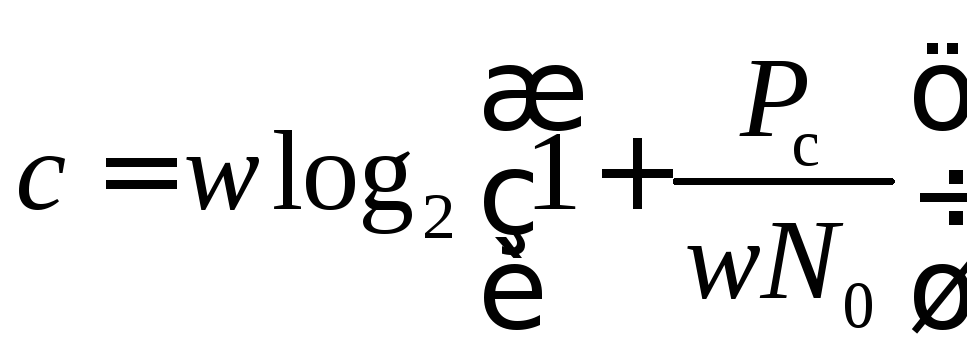При расширении полосы пропускная способность сначала быстро растет (с~w), а затем асимптотически сходится к величине

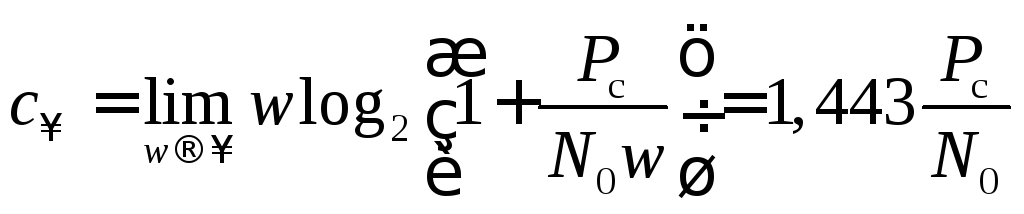
Зависимость представлена графиком рис.11.5.

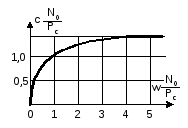
Рис.11.5. Диаграмма обмена нормированной пропускной способности на полосу канала передачи информации

Из , в частности, следует, что для передачи заданного количества информации I=cTс требуемым качеством, отношение энергии сигнала к спектральной плотности аддитивного нормального шумадолжно быть не меньше некоторого порогового значения. Так для передачи 1 бита информации нужно, очевидно, чтобы

.

Удельные затраты полосы пропускания на передачу 1 бита информации

Приняв во внимание, что maxRT=cT=1 бит, а также учитывая и , можно установить, что

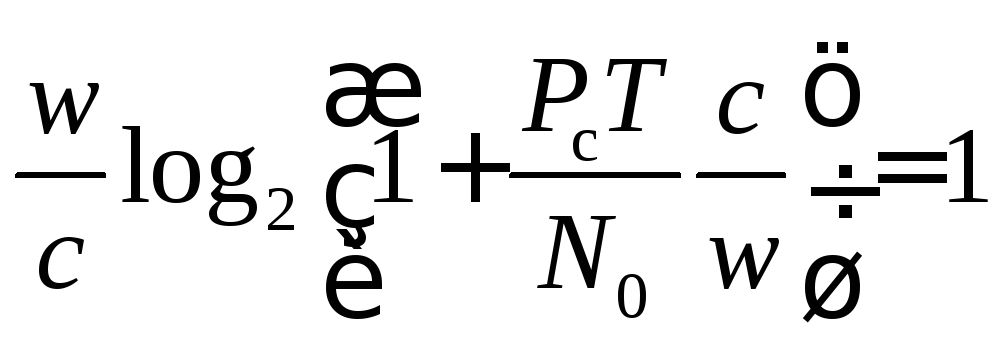
или

.

Зависимость определяет диаграмму обмена между удельными (на передачу 1 бита информации) затратами энергии и полосы в канале с аддитивными гауссовскими шумами. Эта зависимость представлена на рис.2.6. Она называется границей Шеннона и показывает, в какой мере улучшение одного из показателей информационной системы (_Еили_w) приводит к ухудшению другого. Все оптимальные системы, наилучшим образом использующие для передачи информации энергию сигнала и полосу частот, занимаемую его спектром, располагаются на кривой рис.11.6. Все реальные системы - выше кривой. Ниже этой кривой информационные системы работать не могут.

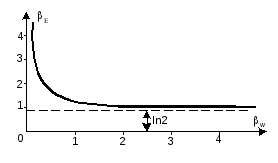
Рис.11.6. Граница Шеннона для гауссовского канала

Обычно информационные системы проектируются с расчетом на работу при сравнительно хороших соотношениях сигнал/шум q>1. Но при этом для справедливо приближение

.

Такая простая зависимость скорости передачи информации от трех переменных w,Тиqпозволяет поставить в соответствие сигналу некоторый объем в трехмерном пространстве рис.11.7.

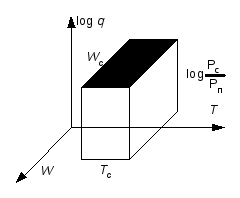
Рис.11.7. Информационный объем сигнала и информационная емкость канала связи

Если рассматриваются спектрально-временные свойства конкретного сигнала, то величина называется его (сигнала) информационным объемом. Если в фигурируют полоса пропусканияw, время наблюденияТи логарифм соотношение сигнал/шум в канале передачи информации, то говорят, чтос– это информационная емкость канала связи.

Такое представление сигнала хорошо иллюстрирует свойство инвариантности сигнала относительно сдвига по времени и/или по оси частот. Действительно, изменение средней частоты сигнала, которому соответствует перемещение всего сигнального объема по оси частот, не изменяет вероятностных характеристик сигнала. То же и при перемещении сигнала по оси времени. Но сжатие сигнала по времени, требует, для сохранения переносимой им информации, пропорционального расширения спектра. Такая деформация называется временной компрессией. Аналогично проявляется и частотная компрессия.