12.7. Процесс с нормальным законом распределения. Центральная предельная теорема

Наиболее распространенной и употребительной моделью случайного процесса является нормальный процесс.

Свойства этого процесса исчерпывающе описывает двумерный закон распределения его мгновенных значений. В ряде задач может быть необходим и многомерный закон, однако он является следствием двумерного закона распределения и может быть определен на его основе.

Нормальным, или гауссовым, называют такой процесс, мгновенные значения которого подчиняются нормальному закону распределения вероятностей с плотностью

,

Где, как и прежде, M{X}– среднее значение случайной величины, а²– ее дисперсия.

Распределение вероятностей нормальной случайной величины

.

Графики зависимостей (2.63) и (2.64) представлены на рис. 12.9.

Рис. 12.9. График нормального одномерного закона распределения случайного процесса при ²=1 иM{X}=3.

Графики построены для частного случая, когда M{X}=3 и²=1. Закон распределения нормальной случайной величины полностью определяется средним значениемM{X} и дисперсией о²и не зависит от других моментов. Если под величинойXпонимается значение случайной функцииX(t) в произвольный момент времени, то и выражают соответственно в дифференциальной и интегральной формах одномерный закон распределения нормального случайного процесса.

Для нормально распределенных случайных величин Х(t) с нулевыми средними значениями и одинаковой дисперсией плотность вероятностей совместного распре деления мгновенных значений вnсечениях можно представить в виде

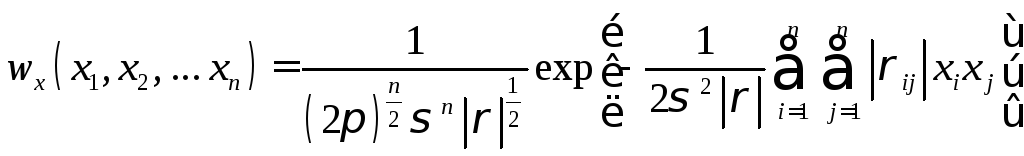
где – алгебраическое дополнение элемента_ijопределителякорреляционной матрицы процессаX(t). Элементами корреляционной матрицы

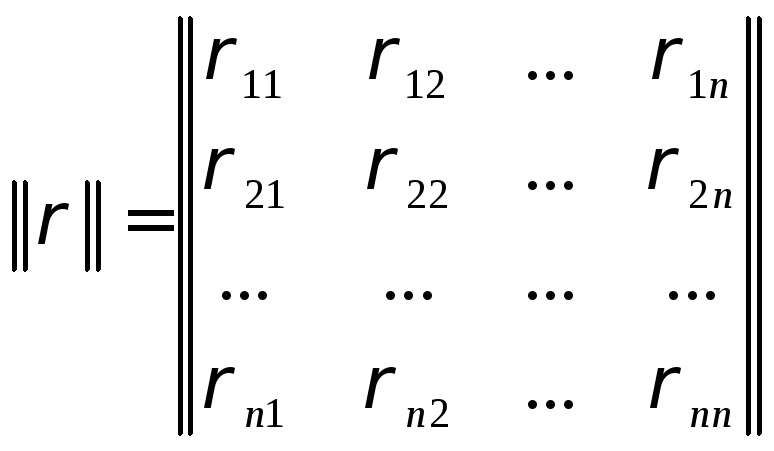
в которой общий член является нормированным коэффициентом корреляции случайных величинX_iиX_j.

Разумеется, в силу симметрии коэффициентов корреляции диагональные члены корреляционной матрицы

₁₂=₂₂=…=_nn=1,

а прочие члены симметричны относительно диагонали. Поскольку случайным величинам придается смысл выборочных значений случайной функции, корреляционная матрица образуется из элементов, которые могут быть вычислены с помощью нормированной функции автокорреляции . Таким образом, функция корреляции однозначно определяет свойства нормального случайного процесса и, в частности, позволяет построить многомерное распределение вероятностей .

В частном случае, когда значения случайной функции берутся через интервалы времени, большие интервала корреляции, можно полагать, что при ijкоэффициент корреляции_ij<1. При этом выражение дляn-мерной совместной плотности распределения вероятностей нормального закона принимает приближенный вид

.

Но поскольку функция автокорреляции полностью определяет многомерное распределение нормального процесса и, как это следует из ее определения, может быть получена с помощью двумерного закона, то двумерный закон распределения нормального случайного процесса полностью определяет его статистические свойства. Из следует выражение для двумерной плотности вероятности значений стационарного нормального процесса Х₁иХ₂, разделенных интервалом:

,

где .

Из и следует выражение для условной плотности вероятности того, что случайный процесс будет иметь мгновенное значение х₂, если за времядо этого его значение было равнох₁. Действительно, подставляя в выражения и , можно получить

.

Ранее отмечалась распространенность нормально распределенных колебаний. Это обусловлено тем, что случайные процессы часто являются результатом суперпозиции большого числа элементарных колебаний, каждое из которых вносит приблизительно одинаковый со всеми остальными вклад в результирующую сумму. В этом случае применима так называемая центральная предельная теорема, согласно которой сумма независимых случайных величин с ростом их числа и независимо от закона распределения каждого из слагаемых становится распределенной нормально. На слагаемые накладывается лишь ограничение на вклад, который они вносят в результирующую сумму. Отдельные слагаемые не должны оказывать заметного влияния на сумму в целом. Если под случайными слагаемыми суммы понимать мгновенные значения элементарных случайных возмущений, формирующих результирующий случайный процесс, то можно сделать вывод о нормальном характере этого процесса. К такому процессу, например, относится шум в цепях приемника, вызванный дискретной природой носителей электричества и непостоянством параметров их движения в электрических цепях. Можно указать и на другие примеры. Так, независимо от статистических свойств процесса, действующего на входе цепи, обладающей способностью интегрировать, на ее выходе случайный процесс по своим статистическим характеристикам будет приближаться к нормальному.

Процессы с нормальным законом распределения обладают рядом особенностей. Линейная комбинация произвольного числа нормальных колебаний также нормальна независимо от параметров законов слагаемых. Следовательно, если нормальный процесс воздействует на линейное устройство, случайное колебание на его выходе сохранит нормальный закон, но с другими параметрами. Сказанное характеризует устойчивость нормального закона.

Для нормального закона, как это следует из , некоррелированность ()=0 означает статистическую независимость:

.

При ином законе распределения вероятностей подобное утверждение не справедливо.

Применительно к нормальным случайным процессам понятия стационарности в узком и широком смысле совпадают.

Отыскание распределения производной по существу эквивалентно отысканию распределения разности двух нормальных случайных величин, расположенных в смежных, весьма близких сечениях. Поэтому производная нормального случайного процесса Y(t)=X'(t) также имеет нормальный закон распределения. Для его записи достаточно иметь функцию корреляции производной, вычисление которой было показано ранее, и по аналогии с формулой записать:

где – дисперсия производной;– ее нормированная функция автокорреляции.

Функция корреляции вычисляется в соответствии с формулой .