2.5. Передаточная функция замкнутой дискретной системы.

Рассмотрим несколько дискретных систем, структурные схемы которых отличаются друг от друга расположением квантователя. Как будет показано ниже, это различие определяет не только вид передаточной функции, но и возможность ее определения.

1. Система с квантованием сигнала ошибки (рис. 17).

Рис.17. Структура замкнутой дискретной САУ

с квантованием сигнала ошибки

Система описывается следующим уравнением в Z-изображениях:

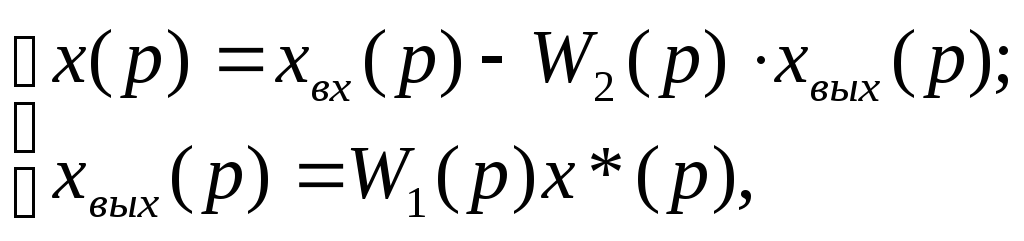(20)

Откуда .

Далее необходимо выполнить над обеими частями последнего равенства. При этом необходимо учитывать, что такое преобразование от произведения импульсной функции (помеченной символом *) и непрерывной функции равно произведению Z-изображений, соответствующих этим функциям.

Следовательно, и .

Выполнив Z-преобразование второго уравнения приведенной выше системы, получим .

Z-изображение выходного сигнала:

а передаточная функция замкнутой системы:

(21)

2. Система с импульсным элементом на выходе (рис. 18).

Рис.18. Структура замкнутой дискретной САУ

с квантованием выходного сигнала

Дискретная система с импульсным элементом на выходе описывается следующими уравнениями:

Подставляя первое из приведенных уравнений во второе, получим:

Z-преобразование последнего выражения дает

откуда

.

В отличие от предыдущей, в данной системе невозможно определить передаточную функцию в виде

.

3. Система с квантованием выходного сигнала и сигнала ошибки (рис. 19).

Рис.19. Структура замкнутой дискретной САУ

с квантованием выходного сигнала и сигнала ошибки

Преобразование Лапласа для сигнала ошибки и выходного сигнала:

.

Z-преобразование над приведенными уравнениями дает:

Z-изображение выходного сигнала:

Следовательно:

а передаточная функция замкнутой системы:

.

Пример 13. Для системы, структура которой приведена на рис. 20, необходимо определить передаточную функцию замкнутой САУ и передаточную функцию по ошибке.

Рис.20. Структура дискретной САУ к примеру 13

Для замкнутой дискретной САУ с квантованием сигнала ошибки дискретная передаточная функция и передаточная функция по ошибке могут быть найдены по следующим формулам:

(22)

(23)

где - дискретные передаточные функции прямого канала и разомкнутой системы, соответственно.

Для системы, рассматриваемой в данном примере:

,

Следовательно,

2.6. Обратное z-преобразование.

Определив дискретные передаточные функции ии, знаяZ-изображение входного сигнала, можно вычислитьZ-изображение выходного сигнала или сигнала ошибки:

.

По Z-изображениям сигналов системы могут быть найдены соответствующие решетчатые функции. Такая операция представляет собой обратноеZ-преобразование, символическое обозначение которой -.

Не следует забывать, что получаемая в результате обратного Z-преобразования решетчатая функцияопределяет значения непрерывного сигналатолько в дискретные моменты времени. Поэтому для полного описания функциинеобходимо использовать дополнительную информацию о поведении системы, либо применять методы, позволяющие вычислить величинувнутри интервалов квантования. К числу таких методов относятся рассматриваемые в последующих разделах данного курса методы дробного квантования и модифицированногоZ-преобразования.

По изображению произвольного вида значениямогут быть вычислены путем разложенияв ряд Лорана (в ряд по убывающим степеням (z)):

(24)

Сравнивая приведенный ряд с (12), получим:

Поскольку для каждого изображения в ряд (24) является единственным, оно может быть осуществлено любым способом, например по формулам:

Наиболее простым приемом нахождения коэффициентов ряда (24) в случае, когда представлено в виде дробно-рациональной функции

(25)

является деление числителя на знаменатель.

Пример 14. Необходимо определить решетчатую переходную функцию системы с передаточной функцией:

Z-изображение решетчатой переходной функции:

В результате деления полинома, стоящего в числителе , на полином в знаменателе, получим:

Коэффициенты полученного степенного ряда определяют следующие дискреты (рис. 21):

;;и т.д.

Использование любого из предложенных методов расчета дискрет решетчатой функции не ограничено какими-либо условиями к виду , но не дает возможности записать выражение дляв виде компактной функции натурального аргумента.

Такая функция может быть получена на основании формулы обратного Z-преобразования (формулы обращения):

.

(26)

Рис.21. Решетчатая переходная функция

(пример 14)

где замкнутый контур интегрирования Г на плоскостиZохватывает особые точки.

Вычисление интеграла (26) может быть осуществлено с использованием формулы Коши в полюсах :

. (27)

Вычет в простом полюсе находится по формуле:

, (28)

а вычет в полюсе кратности S:

. (29)

Если полюса изображения (25) простые, , а полином в числителе может быть представлен в виде, то (27) преобразуется к виду:

.

Пример 15. Необходимо определить выражение для решетчатой функции , если

.

Используя (30), имеем:

Рассчитанные по полученному выражению значения дискрет, как и следовало ожидать, совпадают с вычисленными в предыдущем примере.

Если все условия, ограничивающие применение (30), выполняются, за исключением того, что полином не имеет нулевого корня, то искомая решетчатая функция определяется по формуле:

,

которую можно использовать для . При этом величинуследует находить по теореме о начальном значении.

Пример 16. Необходимо определить выражение для решетчатой функции, если

.

Начальное значение решетчатой функции равно:

.

Для определения предыдущих значений по (31) полагаем:

В соответствии с полученным выражением для имеем:

;и т.д.

Если число нулей равно числу полюсов (25) (порядок полиномов иравны), следует, разделивна, представитьв виде суммы составляющей нулевого порядка и дробно-рационального остатка. При этом первое слагаемое определяет величину, а по второму, используя формулу (31), можно вычислить искомую решетчатую функцию.

Пример 17. Необходимо определить выражение для решетчатой переходной функции разомкнутой дискретной САУ, передаточная функция ПНЧ которой равна:

Передаточная функция дискретной системы:

.

Z– изображение переходной функции:

.

В соответствии с формулой (31) можно записать:

;

;

Начальное значение решетчатой функции: . Длясправедливо:

.

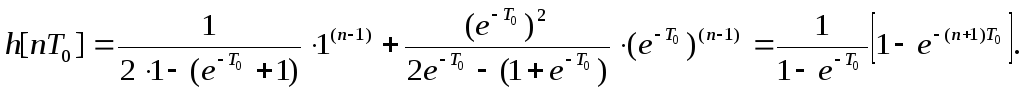Пусть, тогда величины дискрет: и т. д. На рис. 22 приведен график решетчатой функциии возможный вид графика функции(штриховая линия).

Рис.22. Переходная функция к примеру 17