3.3 Критерий устойчивости, использующий билинейное преобразование.

Билинейное преобразование: и(32)

переводит точки единичной окружности на плоскости zв точки, лежащие на мнимой оси плоскостиw, и наоборот. Любой точке, распложенной внутри этой окружности, согласно (32) соответствует точка левой полуплоскостиw, а точки, находящиеся вне окружности, отображаются в точки, принадлежащие правой полуплоскостиw.

Следовательно, условие устойчивости дискретной САУ, связанное с принадлежностью z-корней характеристического уравненияединичному кругу, равносильно условию принадлежности левойw-полуплоскости корней уравнения, полученного из исходного уравнения путем билинейного преобразования (32). Решение такой задачи может быть осуществлено с использованием известных критериев, разработанных для оценки устойчивости непрерывных систем, например критериев Рауса или Гурвица.

Пример 20. Необходимо оценить устойчивость замкнутой дискретной системы второго порядка, характеристическое уравнение которой в общем случае записывается в виде:

Используя билинейное преобразование (32), осуществляем переход к переменной w:

.

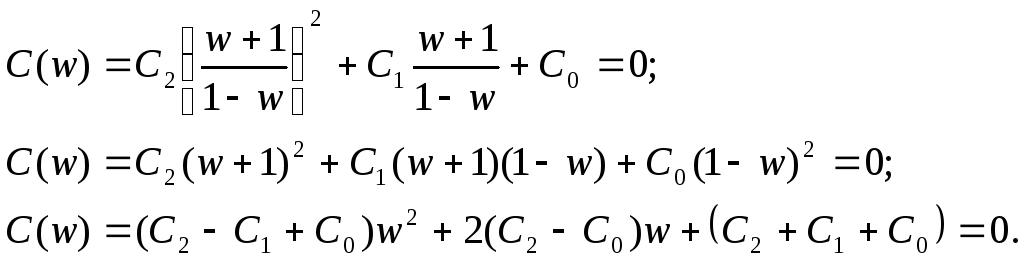Согласно критерию Гурвица необходимым и достаточным условием устойчивости замкнутой САУ является положительность коэффициентов ее характеристического уравнения. Следовательно, условие устойчивости рассматриваемой дискретной системы:

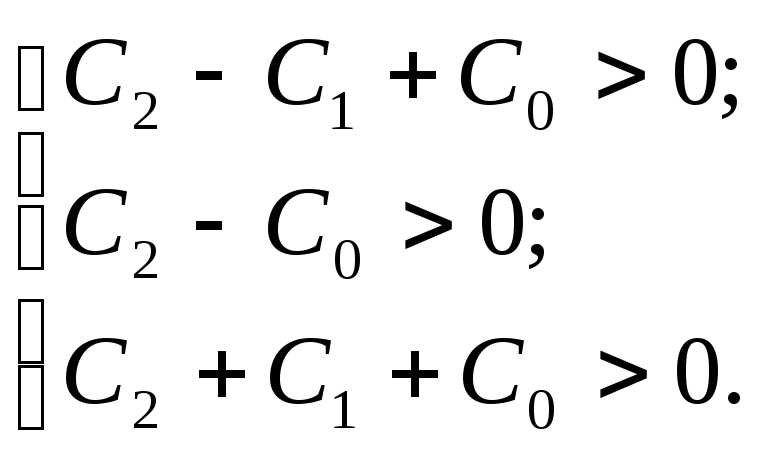
3.4. Абсолютно устойчивые системы.

Дискретные системы с конечным временем регулирования.

Если передаточная функция замкнутой устойчивой дискретной системы описывается дробно-рациональным выражением

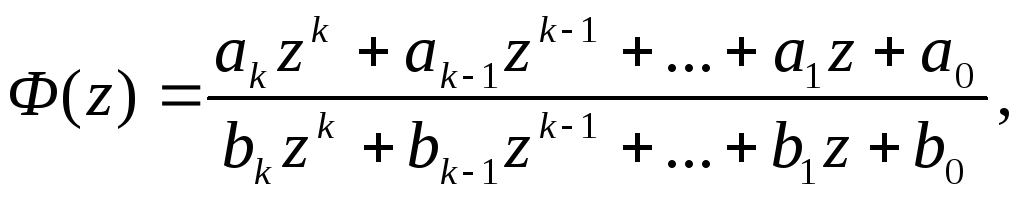
то степень устойчивости такой системы может быть оценена по расстоянию от единичной окружности, проведенной из начала координат плоскости z, до ближайшего к нейz-корня характеристического уравнения

При использовании для описания дискретной САУ комплексной переменной рстепень устойчивости оценивается по расстоянию от мнимой осир-плоскости до ближайшего к нейр-корня характеристического уравнения:

Если первые kмладших коэффициентов характеристического уравнения равны нулю, т.е., оно сводится к виду

Это уравнение имеет корень кратностиk, при этом степень устойчивости оказывается бесконечно большой.

Определим решетчатую функцию на выходе такой абсолютно устойчивой дискретной системыпри подаче на вход единичного ступенчатого сигнала. Для системы второго порядкаZ-изображение выходного сигнала равно:

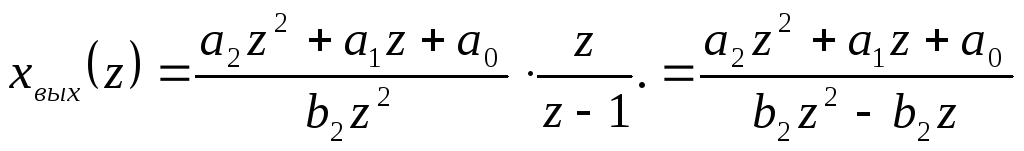
Значения решетчатой функции определим путем разложенияв ряд Лорана:

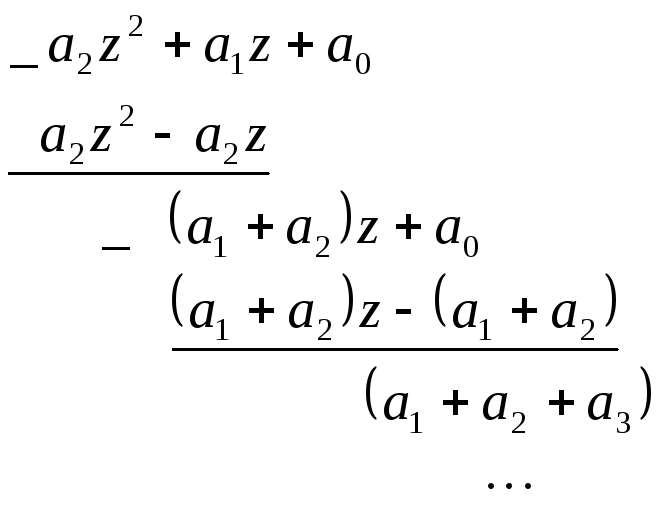
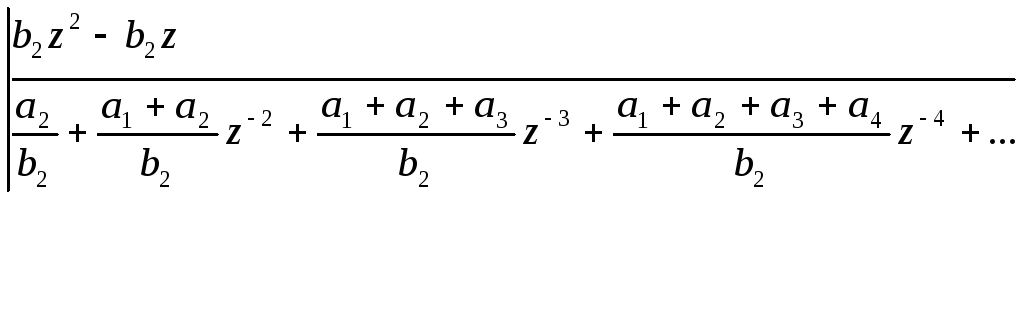
Имеем: ;; при, т.е. выходной сигнал системы, достигнув установившегося значения за два периода квантования, в дальнейшем остается неизменным.

В общем случае для абсолютно устойчивой системы k-го порядка значения решетчатой переходной функции 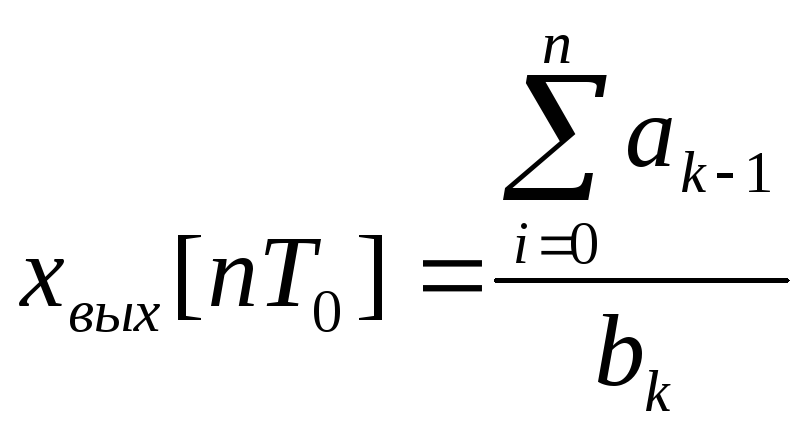при

, а при

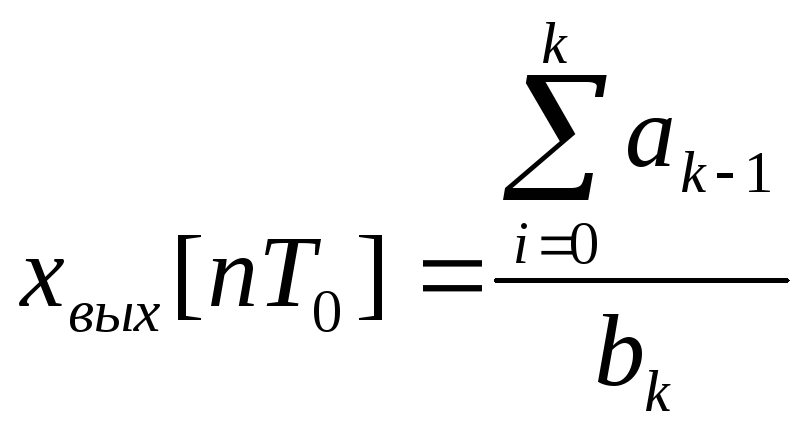
т.е. по истечении kтактов выходной сигнал системы становится постоянным. Следовательно, переходный процесс, вызванный единичным ступенчатым воздействием, заканчивается за конечное время. Необходимо учитывать, что между моментами квантования непрерывный сигналможет содержать пульсации, но при малой величине периода квантованияих амплитуда обычно незначительна.

Пример 21. Необходимо определить значения коэффициентов и, при которых достигается конечная длительность процесса регулирования в дискретной САУ (рис. 24).

Рис.24. Структура дискретной САУ к примеру 21

Дискретная передаточная функция разомкнутой системы:

.

Характеристическое уравнение замкнутой САУ:

или

Следовательно, условие конечной длительности переходного процесса:

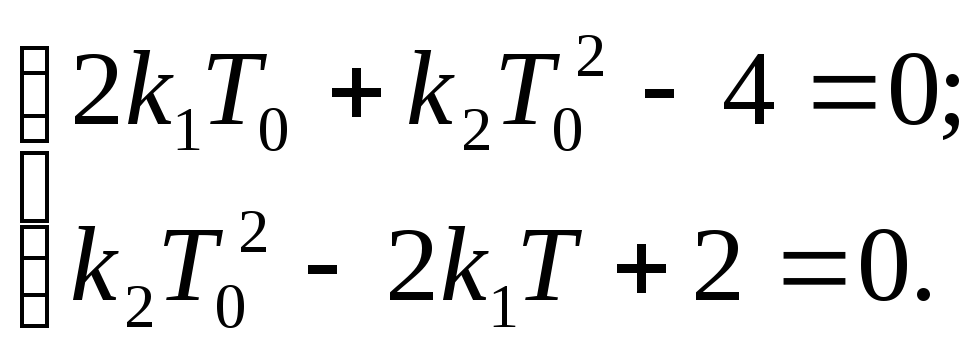
Решение приведенное системы уравнений: ;.

Время переходного процесса: .