§ 1. Декартова реалізація системи аксіом евклідової геометрії (за о.В. Погорєловим)

1.1. Несуперечливість системи аксіом евклідової геометрії

Доведення несуперечливості системи аксіом зводиться до побудови ' хоча б однієї її реалізації (інтерпретації), в якій основні поняття і аксіоми набувають конкретного змісту. Якщо існує хоча б одна така сфера конкретних речей, відношення між якими задовольняють дану аксіоматику, то несуперечливість даної системи аксіом буде такою, якою є несуперечливість об'єктів теорії (науки), через які визнача­ються основні поняття даної системи аксіом. Отже, доведення несу­перечливості даної системи аксіом є умовним.

Множина об’єктів в яких дана системо аксіом знаходить реальне втілення,називається моделлю або інтерпретацією досліджуваної, системи аксіом .

Для побудови реалізації системи аксіом евклідової геометрії, запропонованої О.В. Погорєловим, візьмемо об'єкти множини всих дійсних чисел, тобто основним поняттям і аксіомам цієї системи надамо арифметичний зміст. Така інтерпретація називається декартовою або арифметичною [4,c.100].

Надамо конкретного арифметичного змісту поняттям «точка»,

«пряма», «належати».

Означення 1. Точкою назвемо будь-яку пару дійсних чисел х і у, взятих у певному порядку: (х; у). Числа х і у називатимемо координатами точки.

Означення 2. Прямою назвемо сукупність всіх точок, координа­ти яких задовольняють рівняння , де. Це рівняння називатимемо рівнянням прямої. Пряміх = 0 і у= 0 будемо називати осями координат, а точку (0; 0) - початком ко­ординат.

Означення 5.3. Будемо говорити, що точка належить прямій, якщо її координати задовольняють рівняння прямої.

Покажемо, що при такому конкретному розумінні основних по­нять «точка», «пряма», «належати» для них виконуються аксіоми належності.

1. Доведемо істинність аксіоми І1, яка стверджує, що через дві точки можна провести пряму, і до того ж тільки одну. Нехай і дані точки. Тоді прямою, яка проходить через ці точки, буде пряма, що задається рівнянням , бо координати даних точок задовольняють це рівняння. Доведемо, що ця пряма єдина. Припустимо, що через і проходять дві прямі. Тоді система рівнянь має два розв'язки. Але в такому разі вона має безліч розв'язків і, отже, ці рівняння лінійно залежні тобто відрізняються лише сталим множником. А це означає, що прямі збігаються, тобто через дві точки не можуть проходити дві різні прямі.

2. Доведемо істинність аксіоми 2, яка стверджує, що на кожній прямій існують принаймні дві точки, і існують три точки які не лежать на прямій.

Нехай - рівняння прямої. Тоді один із коефіцієн­тів a і b відмінний від нуля. Нехай, наприклад, . Візьмемо дові­льні числа і знайдемо числаза формулами

Точки ілежать на даній прямій.

Розглянемо точки (0; 0), (0; 1) і (1; 0). Ці три точки не лежать на одній прямій. Справді, припустимо, що вони лежать на деякій прямій . Підставляючи координати точок у це рівняння послі­довно, одержимо с=0;b=0;c=0, що суперечить нашому означенню прямої [1,c.58].

Надамо конкретного арифметичного змісту поняттю «довжина відрізка».

Означення 4. Відстанню між точками (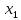; ), () назвемо число

Означення 5. Довжиною відрізка назвемо відстань між його кінцями.

Тоді виконується аксіома існування відрізка даної довжини. Дій­сно, яке б не було дійсне число d > 0. існує відрізок довжини d. Та­ким відрізком буде, наприклад, відрізок з кінцями в точках (0; 0) і (d; 0), оскільки

Перевіримо виконання аксіоми паралельних, а саме: покажемо, що в декартовій реалізації через точку (х₀; y₀) яка лежить зовні пря­мої можна провести не більше однієї прямої, парале­льної їй. Припустимо, що існують дві прямі i які проходять через точку(х₀; y₀) і паралельні даній прямій. Тоді обидві системи рівнянь: i несумісні. Тому їх визначники дорівнюють нулю: .

Звідси випливає, що Оскільки ж система рівнянь

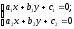
має розв'язок (х₀; y₀),то її рівняння лінійно залежні, тобто відрізняються лише множником. А це означає, що прямі збігаються, що супе­речить умові. Аксіома паралельних, таким чином, у декартовій реа­лізації виконується.

Аналогічно можна показати, що в даній реалізації виконуються всі аксіоми евклідової геометрії, сформульовані О. В. Погорєловим (розділ 4). Перевірку виконання ряду інших аксіом у цій реалізації можна знайти в посібнику [19,c.156].

Ми побудували арифметичну реалізацію системи аксіом евклідо­вої геометрії, надавши основним геометричним поняттям конкрет­ного арифметичного змісту і показавши, що всі аксіоми евклідової геометрії в цій реалізації виконуються. Оскільки аксіоми геометрії у цій реалізації доводилися на основі аксіом арифметики, то питан­ня про несуперечливість системи аксіом евклідової геометрії зводиться до питання про несуперечливість арифметики, тобто евклідова геометрія несуперечлива; якщо несуперечливою є арифметика дійсних чисел. А несуперечливість системи аксіом арифметики підтверджується багатовіковою практикою людства [19,c.157].