2.3. Повнота системи аксіом Вейля

Як уже зазначалося, для доведення повноти системи аксіом треба показати, що будь-які дві її реалізації ізоморфні між собою.

Для доведення повноти системи аксіом Вейля використаємо декартову реалізацію, оскільки в наслідках з аксіом Вейля зазнача­лось, що в просторі можна ввести прямокутну декартову систему координат. [19,c.106].

У системі координат 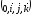координатами точки М простору назвемо координати вектора .При цьому кожній точці М прос­тору ставиться у відповідність упорядкована трійка чисел, причому ця відповідність буде взаємно однозначною.

Якщо точки А і В мають відповідно координати і то вектор матиме своїми координатами числа .

Тепер можна довести, що будь-яка реалізація аксіоматики простору ізоморфна декартовій (арифметичній) реалізації системи аксіом Вейля евклідової геометрії (п. 5.3.1).

Справді, нехай М - деяка довільна реалізація даної аксіоматики. Введемо в цій реалізації прямокутну декартову систему координат і кожній точці, кожному вектору поставимо у відповідність їх координати. Ці ж самі основні об'єкти (вектори і точки) в арифметичній реалізації визначені за допомогою дійсних чисел. З правил операцій над векторами і правил визначення координат вектора за координатами його кінцевих точок випливає, що основні відношення між точками і векторами в обох реалізаціях мають однаковий зміст, тобто довільна реалізація М аксіоматики Вейля ізоморфна арифметичній реалізації. Оскільки поняття ізоморфізму має властивість транзитивності, то звідси також випливає, що будь-які дві інтерпретації аксіом Вейля евклідової геометрії ізоморфні між собою.

Отже, система аксіом Вейля евклідової геометрії є повною [4,c.54].

$ 3. Доведення несуперечливості геометрії Лобачевського

Моделлю геометрії Лобачевського називається поверхня або простір, в якому виконуються аксіоми геометрії Лобачевського.

Так як, всі реалізації геометрії Лобачевського ізоморфні, тому твердження доведене в одній моделі геометрії Лобачевського , буде вірно в будь-якій іншій моделі. Тим самим для проведення міркувань можна щоразу вибирати найбільш «зручну» модель. Наприклад, в конформних моделях Пуанкаре, кут між кривими дорівнює евклідовому куту.

У розділі 2 викладено основні факти планіметрії Лобачевського. Хоча значна кількість цих фактів суперечить нашим звичайним уявленням про властивості прямих, трикутників, чотирикутників, але всі вони виводились правильними логічними міркуваннями. Несуперечливість геометрії, системи аксіом, на якій вона побудована, містить гарантію, що при подальшому розвитку геометрії на основі даної аксіоматики не виникнуть суперечливі твердження. [16,c.239].

При створенні нової геометрії Лобачевський користувався відомими фактами геометрії Евкліда, які не є наслідками п'ятого посту­лату Евкліда, тобто всі твердження, які не залежать від змісту п'ято­го постулату, є спільною частиною геометрії Евкліда і Лобачевського. Користуючись аксіоматикою Гільберта, якої не було за життя Лоба­чевського, можна сказати, що спільною частиною обох геометрій є сукупність всіх тверджень, які можна вивести з аксіом перших чо­тирьох груп системи аксіом Гільберта. Цю спільну частину назива­ють абсолютною геометрією.

Для доведення несуперечливості геометрії Лобачевського, як і інших геометрій, треба побудувати реалізацію системи аксіом, яка складається з аксіом абсолютної геометрії і аксіоми паралельності Лобачевського.

Перша спроба побудови реалізації фактів площини Лобачевсько­го належить італійському геометру Є. Бельгіїрамі (1868), який пока­зав, що в евклідовому просторі є такі поверхні сталої від'ємної кри­вини — псевдосфери, внутрішня геометрія яких збігається з геометрі­єю на площині Лобачевського (локально).

Німецький математик Ф. Клейн удосконалив реалізацію Бельтрамі (1870), і в математиці вона відома під назвою реалізація Бельтрамі — Клейна [10,c.157].