
- •Курсова робота
- •§ 1. Декартова реалізація системи аксіом евклідової геометрії (за о.В. Погорєловим)
- •1.1. Несуперечливість системи аксіом евклідової геометрії
- •1.2. Повнота системи аксіом евклідової геометрії
- •1.3. Незалежність аксіоми існування відрізка заданої довжини
- •1.4. Незалежність аксіоми паралельних.
- •§ 2. Арифметична реалізація векторної системи аксіом г. Вейля евклідової геометрії
- •2.1. Несуперечливість системи аксіом г. Вейля евклідової геометрії для простору те3
- •2.2. Незалежність системи аксіом г. Вейля
- •2.3. Повнота системи аксіом Вейля
- •3.1. Реалізація Бельтрамі - Клейна
- •Реалізація Пуанкаре
- •Висновки
- •Говорячи про несуперечливість системи аксіом, то вона називається незалежною (мінімальною), якщо кожна аксіома даної системи не є логічним наслідком інших аксіом цієї системи.
- •Список використаних джерел
1.4. Незалежність аксіоми паралельних.
У такий же спосіб доведемо незалежність аксіоми паралельних від інших аксіом евклідової геометрії.
Теорема 4. Аксіома паралельних евклідової геометрії незалежна, тобто не може бути виведена як наслідок з інших аксіом.
Рис. 1
Доведення. Згідно із загальним способом доведення незалежності аксіом нам досить побудувати таку реалізацію системи аксіом евклідової геометрії, в якій би виконувались всі аксіоми, крім аксіоми паралельних. Побудуємо таку реалізацію.
Під
точкою будемо розуміти довільну точку
евклідової площини всередині одиничного
круга
 під прямою - довільну хорду цього круга
(рис. 1)Відношення
належності будемо розуміти так, як і в
евклідовій площині. Довжину відрізка
АВ
з
кінцями
під прямою - довільну хорду цього круга
(рис. 1)Відношення
належності будемо розуміти так, як і в
евклідовій площині. Довжину відрізка
АВ
з
кінцями
 визначимо
так. Нехай пряма АВ
перетинає
х2
+ у2=1
в
точках
визначимо
так. Нехай пряма АВ
перетинає
х2
+ у2=1
в
точках
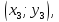
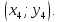 Тоді
довжиною відрізка АВ
назвемо
число
Тоді
довжиною відрізка АВ
назвемо
число
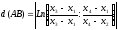
якщо
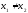 аналогічний
вираз із заміноюх
та
у,
якщо
аналогічний
вираз із заміноюх
та
у,
якщо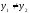 .
У
цій реалізації виконуються всі аксіоми
евклідової геометрії, крім аксіоми
паралельних. Дійсно, через дану точку
круга можна провести безліч хорд, які
не перетинають дану хорду. Побудова
цієї реалізації і доводить незалежність
аксіоми паралельних від інших аксіом
[17,c.63].
.
У
цій реалізації виконуються всі аксіоми
евклідової геометрії, крім аксіоми
паралельних. Дійсно, через дану точку
круга можна провести безліч хорд, які
не перетинають дану хорду. Побудова
цієї реалізації і доводить незалежність
аксіоми паралельних від інших аксіом
[17,c.63].
§ 2. Арифметична реалізація векторної системи аксіом г. Вейля евклідової геометрії
2.1. Несуперечливість системи аксіом г. Вейля евклідової геометрії для простору те3
Основним поняттям системи аксіом Вейля надамо конкретний зміст за допомогою дійсних чисел, тому така реалізація називається арифметичною.
1.
Вектором
назвемо
будь-яку матрицю стовпець вигляду
 де
де
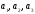 - довільні дійсні числи. При цьому два
вектори збігаються тоді і тільки тоді,
коли відповідні елементи двох матриць
рівні. Збігання векторів позначатимемо
знаком рівності.
- довільні дійсні числи. При цьому два
вектори збігаються тоді і тільки тоді,
коли відповідні елементи двох матриць
рівні. Збігання векторів позначатимемо
знаком рівності.
2.
Точкою
назвемо
будь-яку матрицю-рядок вигляду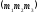 де
де
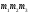 -
довільні
дійсні числа. При цьому дві точки
-
довільні
дійсні числа. При цьому дві точки
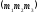 і
і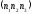 збігаються
тоді і тільки тоді, коли
збігаються
тоді і тільки тоді, коли
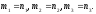 .
.
3.
Сумою
векторів
i
 назвемо вектор
назвемо вектор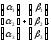
4.
Добутком
числа k
на вектор
 назвемо вектор
назвемо вектор

5.
Скалярним
добутком
векторів
 і
і
 ,
встановленим ненульовим вектором
,
встановленим ненульовим вектором
 називається число.
називається число.
6.
Належність упорядкованої пари точок
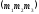 і
і
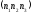 вектору
вектору визначається
умовою
визначається
умовою
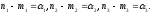
Можна
переконатись, що при таких означеннях
основних об'єктів і основних відношень
всі аксіоми Вейля тривимірного евклідового
простору виконуються. Перевірка аксіом
першої, другої, третьої і четвертої груп
майже тривіальна, якщо взяти за нульовий
вектор
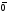 матрицю-стовпчик
матрицю-стовпчик (аксіома 1.3)б а за три лінійно незалежні
вектори (аксіома 4.1) матриці стовпці
(аксіома 1.3)б а за три лінійно незалежні
вектори (аксіома 4.1) матриці стовпці
 Перевіримо реалізацію аксіом 1 і 2
[15,c.303].
Перевіримо реалізацію аксіом 1 і 2
[15,c.303].
Аксіома
1.
Нехай А
=
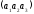 -довільна
точка і
-довільна
точка і
 -довільний
вектор.
-довільний
вектор.
Треба
довести, що існує одна і тільки одна
точка
 -
-
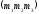 така,
що вектор
така,
що вектор
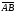 =
=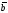 .За
означенням належності (6)
при
цьому має виконуватись умова:
.За
означенням належності (6)
при
цьому має виконуватись умова: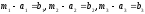 З
цієї умови випливає, щ
о
існує одна і тільки одна трійка чисел
З
цієї умови випливає, щ
о
існує одна і тільки одна трійка чисел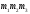 ,
яка задовольняє ці числові рівності.
,
яка задовольняє ці числові рівності.
Аксіома
2.
Нехай
маємо три довільні точки

 ,
,
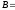
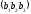 ,
,

 .
.
За
домовленістю
(6)
знаходимо
вектори
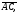

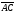 :
:
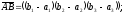

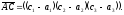
Тоді
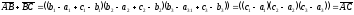 Аксіома
2
доведена.
Аксіома
2
доведена.
Отже система аксіом Вейля. а тому і геометрія Евкліда, несуперечлива настільки, наскільки несуперечливою, є арифметика дійсних чисел [9,c.180].
2.2. Незалежність системи аксіом г. Вейля
Як уже зазначалось, несуперечлива система аксіом називається незалежною (мінімальною), якщо кожна аксіома даної системи не є логічним наслідком інших аксіом цієї системи.
Нехай
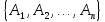 -
дана
система аксіом геометрії. Для доведення,
наприклад, незалежності аксіом
-
дана
система аксіом геометрії. Для доведення,
наприклад, незалежності аксіом
 від
аксіом
від
аксіом
 треба
побудувати нову
систему
аксіом
треба
побудувати нову
систему
аксіом
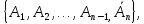 де
де
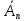 -заперечення
аксіоми
-заперечення
аксіоми
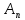 ,
і
довести її несуперечливість. Якщо
аксіома
,
і
довести її несуперечливість. Якщо
аксіома
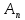 є
наслідком аксіом
є
наслідком аксіом
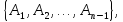 то вона
буде наслідком із
системи
то вона
буде наслідком із
системи
 ,
тобто в цій новій аксіоматиці аксіому
,
тобто в цій новій аксіоматиці аксіому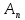 можна
довести як теорему. Отже, у новій
аксіоматиці матимуть місце два
суперечливих між собою твердження
можна
довести як теорему. Отже, у новій
аксіоматиці матимуть місце два
суперечливих між собою твердження
 i
i
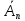 ,
але
тоді ця
аксіоматика
не буде несуперечливою [17,c.157].
,
але
тоді ця
аксіоматика
не буде несуперечливою [17,c.157].
Розглянемо декілька прикладів доведення незалежності окремих аксіом Вейля.
1.
Доведення незалежності аксіоми 4.1 від
аксіом простору .
.
Треба довести несуперечливість системи аксіом
(1.1-1.4,2.1-2.4,
3.1-3.5, 4.2.5.1,
5.2},
(1)
4.2.5.1,
5.2},
(1)
де
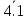 - заперечення
аксіоми 4.1.
- заперечення
аксіоми 4.1.
Для
цього використаємо арифметичну
реалізацію, побудовану для доведення
несуперечливості системи аксіом Вейля
простору
 але
внесемо до неї деякі зміни:вектором
назвемо
будь-яку матрицю-стовпчик
але
внесемо до неї деякі зміни:вектором
назвемо
будь-яку матрицю-стовпчик
 ,
де
,
де
 і
і - довільні дійсні числа, скалярним
добутком векторів
- довільні дійсні числа, скалярним
добутком векторів i
i
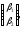 встановленим ненульовим вектором
встановленим ненульовим вектором
 назвемо
число
назвемо
число
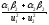
При
таких домовленостях всі аксіоми системи
(1) виконуються, зокрема аксіома
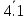 виконується
тому, що в даній реалізації не виконується
аксіома 4.1, оскільки будь-які три вектори
лінійно залежні.
виконується
тому, що в даній реалізації не виконується
аксіома 4.1, оскільки будь-які три вектори
лінійно залежні.
Аналогічно доводиться незалежність аксіоми 4.2.
2. Доведення незалежності аксіоми 1 від аксіом Вейля простору ТЕ3.
Треба довести несуперечливість системи аксіом
{1.1
- 1.4,2.1 - 2.4, 3.1 - 3.5, 4.1 - 4.2,
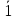 ,5.2}
(2)
,5.2}
(2)
де
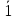 -
заперечення аксіоми 1.
-
заперечення аксіоми 1.
Використаємо
арифметичну реалізацію, побудовану для
доведення несуперечливості системи
аксіом Вейля простору
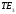 ,
але
внесемо такі зміни:
,
але
внесемо такі зміни:
Точкою назвемо матрицю виду
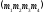 де
де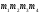 довільні
дійсні числа. При цьому точки
довільні
дійсні числа. При цьому точки
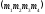 i
i
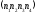 збігаються
тоді і тільки тоді, коли
збігаються
тоді і тільки тоді, коли
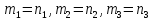 ,
,
належність упорядкованих пар точок
 i
i
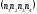 вектор
вектор визначається умовами
визначається умовами
 У
видозміненій у такий спосіб інтерпретації
будуть виконуватись всі аксіоми Вейля,
крім аксіоми
1.
Аксіома 1
не виконується тому, що визначення
належності впорядкованої пари точок
і вектора числа
У
видозміненій у такий спосіб інтерпретації
будуть виконуватись всі аксіоми Вейля,
крім аксіоми
1.
Аксіома 1
не виконується тому, що визначення
належності впорядкованої пари точок
і вектора числа
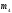 і
і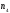 не
фігурують, вони можуть вибиратись
довільно.
не
фігурують, вони можуть вибиратись
довільно.Доведення незалежності аксіоми 2.
Для
доведення належності аксіоми
2
в арифметичній інтерпретації п.
5.3.1
умову належності
упорядкованої
пари точок
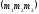 і
і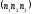 вектора
вектора
 сформулюємо так :
сформулюємо так :
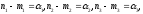
Тоді в такій інтерпретації всі аксіоми Вейля виконуються, крім аксіоми 2, у чому легко переконатися.
Аналогічно можна пересвідчитися у незалежності інших аксіом Вейля. [18,c.140].
