Специально для групп С-12 / Общая физика_под ред. Белокопытова_2016 -506с

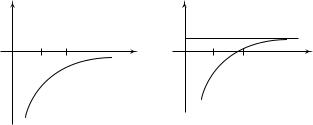
					º
при прямолинейном движении. На малом перемещении d r						элемен-
тарная работа
δA =	º º	= Fdr cos π = –Fdr .
	F d r
Тогда изменение потенциальной энергии
2	2	2	Mm	1	1	.
Wп = –∫δA = ∫Fdr
		= ∫G ---------		dr = GMm ----	– ----
1	1	1	r 2	r1	r2

Рассмотрим на данном примере выбор нулевого уровня потенциальной энергии.

Первый способ. В физике часто встречаются силы, модуль которых с увеличением расстояния между взаимодействующими телами уменьшается и при r → × достаточно быстро стремится к нулю. К таким силам относится сила гравитационного взаимодействия. В таких задачах обычно потенциальную энергию принимают равной нулю «на бесконечности», т.е. в положении системы, когда тела удалены одно от другого бесконечно далеко. Пусть в рассматриваемом примере точка 2 находится «на бесконечности», тогда Wп 2 = 0. В этом случае получим:

Wп1 = – GMm ⁄ r1 или Wп = – GMm ⁄ r .

Этой зависимости потенциальной энергии гравитационного взаимодействия материальной точки т, находящейся на произвольном расстоянии r от массы М, соответствует график, показанный на рис. 3.7, а.

Второй способ. Примем потенциальную энергию системы равной нулю во втором положении системы, т.е. при r = r2 . Тогда Wп 1 =

= – GMm ⁄ r1 + GMm ⁄ r2 , причем второе слагаемое в этой формуле

— некоторая постоянная величина: GMm ⁄ r2 = C. Потенциальная

Wп			Wп
r1	r2		С
0		r	0	r1	r2	r
	а)				б)
		Рис. 3. 7

41

энергия гравитационного взаимодействия на произвольном расстоянии r между телами может быть представлена в виде Wп =

= – GMm ⁄ r1 + C . График, соответствующий этой зависимости, представлен на рис. 3.7, б.

Из последней формулы видно, что потенциальная энергия определена с точностью до некоторого постоянного значения, которое зависит от выбора нулевого потенциального уровня. Этот выбор в каждой конкретной задаче осуществляется индивидуально. При этом, решая задачу, обычно исходят из того, что выражение потенциальной энергии в произвольной конфигурации системы должно выглядеть наиболее просто. Поэтому в нашем примере первый способ выбора нулевого потенциального уровня является наиболее рациональным, а потому и общепринятым.

В качестве еще одного примера рассмотрим гравитационное поле Земли, радиус которой R, а масса М. Можно показать, что если расстояние до центра Земли r > R, то гравитационное поле, создаваемое Землей, такое же, как если бы вся масса Земли была бы сосредоточена в ее центре. Пусть тело массы т перемещается из точки 1, находящейся на расстоянии r1 = R от центра Земли, в точку 2, находящу-

юся на высоте h над поверхностью планеты (r2 = R + h). Найдем

изменение его потенциальной энергии. Выберем нулевой альный уровень на поверхности Земли в точке 1. Тогда Wп 1

довательно, W	= GMm	1	1	=	GMmh	.
		-----	– ------------------		R----------------------(R + h)
п2		R (R + h)

потенци- = 0. Сле-

Если h << R, то Wп2 = GMmh ⁄ R2 , а так как g = GM ⁄ R2 , то Wп 2 = mgh. Эта формула часто использовалась в школьных задачах. Обратите внимание на условие, при котором она справедлива!

Рассмотрим потенциальную энергию упруго деформированной пружины. Пусть пружина имеет жесткость k, тогда упругая сила записывается в соответствии с выражением (2.6). Пусть пружина растянута на длину х. Найдем изменение потенциальной энергии:

2	º º
Wп = – ∫	Fупр d r
1

x	º	x
= – ∫	Fупр dx cos π = – ∫kx dx cos π = kx2 ⁄ 2 .
0		0

Если нулевой уровень отсчета потенциальной энергии выбрать в том положении, когда пружина не растянута, то

Wп = kx2 ⁄ 2 .

42

3.5. Дифференциальная связь между потенциальной силой и потенциальной энергией. Понятие градиента

В § 3.4 была получена интегральная связь между изменением потенциальной энергии и потенциальной силой:

	2 º	º
	Wп = – ∫ F
		пот d r .
	1
	Решим обратную задачу: зная значение потенциальной энергии

(по отношению к заранее выбранному нулевому уровню), которой обладает материальная точка, помещенная в силовое потенциальное поле, найдем значение потенциальной силы. Рассмотрим бесконечно

º	. Изменение потенциальной энергии на этом
малое перемещение d r
перемещении будет
º	º		d y + Fz dz).
dWп = – F d r		= – (Fx dx + Fy
Пусть перемещение тела происходит только вдоль оси ОХ так,
		dWп
		----------	. Производная функции,
что y = const и z = const. Тогда Fx = – dx

когда при дифференцировании по одной из переменных (в нашем случае по х) остальные переменные считаются постоянными, назы-

вается частной производной и обозначается

∂

∂x . Таким образом, Fx =

-----

= –

∂Wп

. Аналогично,

Fy = –

∂Wп

и

Fz = –

∂Wп

. Тогда вектор силы

---------

---------

---------

∂x

∂y

∂z

можно представить следующим образом:

º

º

º

º

º

∂Wп

º

∂Wп

º ∂Wп

. (3.9)

F

= i F +

j F

+ k F

= – i

---------

+ j

---------

+ k ---------

x

y

z

∂x

∂y

∂z

Вектор, компоненты которого равны соответствующим частным производным скалярной величины по координатам, носит название

градиента скалярной функции (обозначается символом grad). Таким образом,

º
F = – grad Wп .	(3.10)

Часто для обозначения градиента вводят так называемый оператор Гамильтона, равный по определению

º	º	-----∂
	= i	∂x

º∂

+j -----

∂y

º	∂	(3.11)
+ k	------ .
	∂z

43

Потенциальную силу можно представить следующим образом:

º	º
F	= – Wп.	(3.12)

Можно показать (это будет сделано в курсе математики), что вектор

º

Wп направлен в сторону максимального возрастания функции Wп .

3.6. Закон сохранения механической энергии

Рассмотрим систему материальных точек, между которыми могут действовать как потенциальные, так и непотенциальные силы. Эти

º

силы могут быть как внешними (обозначим их F ), так и внутрен-

º

ними (обозначим их f ). Воспользуемся теоремой об изменении кинетической энергии для системы материальных точек (3.6):

º º º º

Wк = A( f п) + A( f неп) + A( Fп ) + A( Fнеп ) ,

где Wк — изменение кинетической энергии рассматриваемой сис-

º

темы; A( f п) — сумма работ всех внутренних потенциальных сил;

º

A( f неп ) — сумма работ всех внутренних непотенциальных сил;

º

A( Fп ) — сумма работ всех внешних потенциальных сил;

º
A( Fнеп ) — сумма работ всех внешних непотенциальных сил.
Перепишем равенство следующим образом:
º	º	º	º

Wк + [– A( f п)] + [– A( Fп )] = A( f неп ) + A( Fнеп) .

º

Слагаемое [– A( f п )] представляет собой изменение потенциальной энергии взаимодействия тел системы за счет работы внутренних

º

потенциальных сил. Слагаемое [– A( Fп )] представляет собой изме-

нение потенциальной энергии взаимодействия тел системы за счет работы внешних потенциальных сил. Можно записать в целом, что

º	º
Wп = – A( f п ) – A( Fп ) . Тогда теорему об изменении кинетической
энергии можно представить следующим образом:
	º	º

Wк + Wп = A( f неп) + A( Fнеп ) .

44

Поскольку сумма кинетической и потенциальной энергий называ-

ется механической энергией, то	Wк +	Wп =	Wмех . Оконча-
тельно можно сформулировать равенство:
º	º
Wмех = A( f неп ) + A( F		неп ) .	(3.13)

Таким образом, изменение механической энергии системы материальных точек равно сумме работ внутренних и внешних непотенциальных сил. Выражение (3.13) является математической записью

закона сохранения механической энергии.

Закон сохранения механической энергии утверждает, что если работа внутренних и внешних непотенциальных сил равна нулю, то механическая энергия системы не меняется.

З а м е ч а н и е 1. Данный вывод справедлив, если потенциальные силы являются стационарными, т.е. если их модуль и направление не зависят от времени.

За м е ч а н и е 2. Если внутри системы действуют только стационарные потенциальные силы, то система называется консервативной. Можно сказать, что механическая энергия сохраняется, если система консервативная и замкнутая. Однако это требование более сильное, чем то, которое требуется в нашем условии выполнимости закона сохранения механической энергии.

За м е ч а н и е 3. Если внутри системы или на нее действуют диссипативные силы, то механическая энергия системы сохраняться не может, если не работают внешние силы, работа которых восполняет убыль энергии в системе.

За м е ч а н и е 4. Закон сохранения механической энергии справедлив только в инерциальной системе отсчета. Это следует из того факта, что закон был получен на основании теоремы об изменении кинетической энергии, которая сама являлась следствием второго закона Ньютона, который выполняется в инерциальной системе отсчета.

За м е ч а н и е 5. Можно показать, что закон сохранения механической энергии следует из однородности времени, которая проявляется в том, что разные моменты времени одинаковы. Это означает, что два одинаковых эксперимента, поставленные в одинаковых условиях, приведут к одному и тому же результату.

За м е ч а н и е 6. Следует еще раз подчеркнуть, что общефизический закон сохранения энергии справедлив всегда без ограничений.

45

Г л а в а 4

ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА

Рассматривая вращательное движение твердого тела, состоящего из совокупности материальных точек, необходимо сделать важные замечания, которые свидетельствуют о сложности использования ранее полученных динамических уравнений для описания движения тела. Во-первых, для описания вращательного движения совокупности материальных точек весьма сложно использовать систему уравнений второго закона Ньютона, записанных в виде (2.2). При вращении точек вокруг какой-либо оси ускорения всех точек тела отличаются и по направлению, и по модулю. Во-вторых, в этом случае сложно использовать и систему динамических уравнений в виде (2.10), т.е. второй закон Ньютона, записанный в терминологии «импульсов». При вращении точек твердого тела вокруг оси даже с постоянной угловой скоростью линейные скорости точек, а значит, и импульсы, различаются и по модулю, и по направлению. Введем новые физические величины, характеризующие вращение твердого тела.

4.1. Момент импульса точки относительно полюса

Рассмотрим вращение материальной точки массой т вокруг неко-

º

торой оси по окружности радиусом R под действием силы F

(рис. 4.1). Положение точки определяется радиусом-вектором ºr , проведенным из произвольного полюса О, лежащего на оси вращения.

	ω
	v
	r
R	F
	m

r

r

O

Рис. 4. 1

46

Запишем для данной точки выражение второго закона Ньютона:

dºv º m --------- = F .

d t

Умножим обе части этого уравнения векторно на ºr :

	º
º	dv	º	º	(4.1)
r	× m --------- = r		× F .
	d t

Левую часть полученного выражения можно представить в виде

	º
º	dv	d	º º	] .
r	× m --------- = ----		[ r , m v
	d t	d t

Векторное произведение радиуса-вектора материальной точки, проведенного из полюса, на импульс этой точки называется моментом импульса материальной точки относительно полюса:

º	º º	] .
lO	= [ r , m v		(4.2)

Таким образом, левая часть выражения (4.1) определяет скорость изменения момента импульса материальной точки относительно полюса.

Чтобы проанализировать модуль и направление вектора момента

импульса, учтем соотношение (1.13). Разложим вектор ºr на два взаимно перпендикулярных вектора, один из которых сонаправлен с

осью вращения (обозначим его ºrC), а другой — перпендикулярен ей

(обозначим его ºrB) (рис. 4.1). Тогда

º	º º	º	º	º	º º	º º
v	= ω × r =	ω × ( rC		+ rB) =	ω × rC	+ ω × rB.

Поскольку векторы ºω и ºrC параллельны, то их векторное произведение равно нулю. Таким образом,

º	º º
v	= ω × rB.

Получаем выражение для момента импульса точки в виде

º	º º	º º	º	º º º
lO	= [ r , m v	] = m[ r , v	] = m[( rB	+ rC ), [ ω, rB]] .

Поскольку векторное произведение обладает дистрибутивностью, то

ºlO = m[( ºrB + ºrC ), [ ºω, ºrB]] =

º º º	º	º º
= m[ rB, [ ω, rB]] + m[ rC		, [ ω, rB]] .	(4.3)

47

Полученные в правой части уравнения слагаемые в математике называются двойным векторным произведением. В курсе векторной алгебры доказывается, что результат двойного векторного произведения — это вектор, определяемый по следующему правилу:

º	º º	º º º	º º º
[ a	, [ b, c	]] = b ( a , c	) – c ( a , b ) .

Первое слагаемое выражения (4.3) перепишем в таком виде:

m[ ºrB, [ ºω, ºrB]] = m( ºω( ºrB, ºrB) – ºrB( ºrB, ºω )) .

Напомним, что скалярное произведение вектора самого на себя равно квадрату модуля вектора: ( ºrB, ºrB) = rB2 . Направления векто-

ров ºrB и ºω указаны на рис. 4.1, эти векторы перпендикулярны

один другому, поэтому скалярное произведение ( ºrB, ºω ) равно нулю. Окончательно имеем:

m[ ºrB, [ ºω, ºrB]] = mrB2 ºω .

Из полученного выражения следует, что одна составляющая вектора момента импульса материальной точки относительно произвольного полюса, лежащего на оси вращения, сонаправлена с вектором угловой скорости этой точки при ее вращении вокруг оси,

º

обозначим ее lOC :

º	2	º
lOC	= mrB	ω .	(4.4)

Рассмотрим другую составляющую — второе слагаемое выражения (4.3):

m[ ºrC, [ ºω, ºrB]] = m( ºω( ºrC, ºrB) – ºrB( ºrC, ºω )) .

Поскольку ºrC ºrB, то ( ºrC, ºrB) = 0 , а поэтому m[ ºrC, [ ºω, ºrB]] =

= – mrCω ºrB. Таким образом, вторая составляющая вектора момента

импульса материальной точки относительно произвольного полюса, лежащего на оси вращения, перпендикулярна оси вращения и

º

направлена к центру вращения. Обозначим ее lOB :

º	º
lOB = – mrC ω rB.		(4.5)

48

Объединив выражения (4.4) и (4.5), запишем уравнение для определения момента импульса материальной точки относительно полюса:

º	º	º	2	º	º
lO =
	lOC + lOB = mrB			ω – mrC	ω rB .	(4.6)
Последнее равенство		проиллюстрировано			на рис. 4.2.	Размер-

ность момента импульса в СИ: [lO ] = кг æм2æс–1.

Вернемся к выражению (4.1) и рассмотрим его правую часть. Векторное произведение радиуса-вектора точки, проведенного из полюса, на вектор силы называется моментом силы относи-

			º
тельно полюса, которое обозначается MO				:
º		º	º
MO	=	r	× F .	(4.7)

Модуль момента силы (рис. 4.3) MO = rF sin α = Fh, где h = r sin α —

длина перпендикуляра, опущенного из точки О на линию действия силы, — называется плечом силы. Рассмотрим основные свойства

º

вектора MO .

1.Момент силы относительно полюса не меняется при переносе силы вдоль линии ее действия, поскольку при этом не меняется плечо силы.

2.Момент равнодействующей нескольких сил равен сумме моментов каждой силы относительно полюса. Действительно, согласно свойству дистрибутивности векторного произведения

º º	º	º	º	N	º	N	º	º	N	º
MO( R ) = r		× R	= r	× ∑	Fi	= ∑ ( r		× Fi ) = ∑		MOi .
				i = 1		i = 1			i = 1

ω lO

MO(F )

lO

v

r

lO

O

F

r

α

r

h

O

Рис. 4. 2

Рис. 4. 3

49

Таким образом, выражение (4.1) может быть может быть записано в виде

	º
	d l O	N º
	----------	= ∑ MOi,	(4.8)
	d t

i = 1

т.е. скорость изменения момента импульса материальной точки равна суммарному моменту сил, действующих на нее. Соотношение (4.8) называется основным уравнением динамики вращательного движения материальной точки или уравнением моментов.

В качестве примера можно рассмотреть движение планеты вокруг Солнца под действием гравитационной силы. Момент, создаваемый силой гравитации относительно полюса, расположенного в центре орбиты (Солнце), определяется по формуле

º		º	×	º
MO	=	r		Fгр.
				º	||	º		,
Поскольку центральная сила направлена к центру, то r						F	гр

º× º

апоэтому r Fгр = 0. Следовательно, момент импульса планеты

º	º	º	] = const. Таким образом, либо планета будет двигаться
lO	= [ r , mv

по окружности (когда r = const) c постоянной по модулю скоростью, либо по некруговой, но плоской траектории (чтобы осталось посто-

º

янным направление вектора lO ). Вывод: материальная точка в поле центральных сил может двигаться только по плоской траектории.

4.2. Момент импульса системы материальных точек относительно полюса

Составим для системы материальных точек основное уравнение динамики вращения вокруг общей оси. Запишем для каждой точки системы соотношение (4.8):

º
d lO1	º º
-------------	= [ r1, R1];
d t
º
d lO2	º º
-------------	= [ r2, R2];
d t
…
º
d lON	º º
-------------	= [ r N , RN],
d t

50