Специально для групп С-12 / Общая физика_под ред. Белокопытова_2016 -506с

6.4. Механическая энергия гармонических колебаний

Рассмотрим механические колебания пружинного маятника, совершающего свободные гармонические колебания, описываемые уравнением x(t) = A cos (ωt ). Полная механическая энергия такого маятника в произвольный момент времени является суммой потенциальной энергии упругой деформации пружины Wп и кинетической

энергии груза Wк .

Выразим кинетическую энергию груза на пружине:

W		=	mv	2	=	m	dx		2	=	mω2A2	sin	2	(ωt) =	kA2	sin	2	(ωt) .
			----------			----- -----					------------------				---------
	к		2			2	dt				2				2

Найдем потенциальную энергию упругодеформированной пружины:

W		=	1	=	mω2x2	=	kA	2	cos	2	(ωt).
	п		---- kx 2		-----------------		---------
			2		2		2

Графики зависимостей потенциальной и кинетической энергии гармонических колебаний от времени показаны на рис. 6.6. Следует

отметить, что частота колебаний энергии ω* = 2ω , а ее максимальное значение пропорционально квадрату амплитуды смещения материальной точки.

x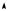

Tt

Wк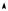

Tt

Wп

Tt

Рис. 6. 6

81

Wп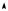

B

W

Wк

Wп

–A

0

A

x

Рис. 6. 7

Полная механическая энергия при свободных колебаниях не изменяется:

W = Wк + Wп = mω2A2 ⁄ 2 = kA2 ⁄ 2 = const , поскольку в системе отсутствуют диссипативные силы.

Рассмотрим движение шарика в гладком параболическом желобе. На рис. 6.7 показано соотношение между потенциальной и кинетической энергиями в зависимости от положения шарика в «потенциальной яме». Если смещение шарика от положения устойчивого равновесия x = 0, то его кинетическая энергия достигает максимума, а потенциальная обращается в нуль. Когда смещение шарика x = ± A (точки поворота), кинетическая энергия обращается в нуль, потенциальная же энергия достигает максимума. При движении смещение шарика может принимать значения x ≤ A . С позиций закона сохранения энергии шарик не может оказаться за пределами этой области, например в точке В. В этом случае его кинетическая энергия приняла бы значение Wк = W – Wп < 0, что невозможно.

6.5. Затухающие колебания

Рассмотрим пружинный	маятник, на		который действует сила
			·
сопротивления, линейно зависящая от скорости Fтр = – μv = –μx .
Векторное уравнение второго закона Ньютона примет вид:
º	º	º	º
m a =	m g	+ Fупр +	Fтр .
Запишем второй закон Ньютона в скалярном виде:
··			·

mx = mg – k( l + x) – μx .

82

Тогда дифференциальное уравнение затухающих колебаний выглядит следующим образом:

··	μ	·	k
	----		----	,
x +	m x +		m x = 0

где μ / m = 2β (β — коэффициент затухания); k / m = ω20 (ω0 —

собственная частота свободных гармонических колебаний).

Дифференциальное уравнение свободных затухающих колебаний линейной системы имеет вид

d2x		dx	2
--------		-----	+ ω0x = 0 .
dt	2	+ 2β dt

Если затухание невелико (β < ω0 ), решением этого однородного линейного дифференциального уравнения является функция

x(t) = A0e– βt sin (ωt + ϕ0 ) ,

т.е. затухающие колебания не являются периодическими, однако величина x(t) обращается в нуль, а также достигает максимальных и минимальных значений через равные промежутки времени

T =	2-----π- = ------------------------	2π - ,		(6.10)
	ω	ω2	– β2
		0

где T — период затухающих колебаний; ω = 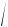ω20 – β2 — частота затухающих колебаний.

Величина x(t) = A0e– βt называется амплитудой затухающих колебаний; A0 — начальная амплитуда. Амплитуда затухающих

колебаний уменьшается с течением времени тем быстрее, чем больше коэффициент затухания β.

Если сравнить амплитуды колебаний системы в моменты времени t и t + τ, то можно получить, что

A(t)	βτ
--------------------	= e .
A(t + τ )

Если за промежуток времени τ амплитуда колебаний уменьшается в е раз, то β = 1/τ, т.е. коэффициент затухания — величина, обратная промежутку времени τ, в течение которого амплитуда затухающих колебаний уменьшается в e раз.

83

x				Также для количественной характе-
				ристики быстроты убывания амплитуды
				затухающих колебаний вводится понятие
				логарифмического декремента δ:
				A(t)	βT	= βT .
				δ = ln -------------------- = ln e
				A(t + T)
0				Если за время NT система совершит N
		t
				колебаний и их амплитуда уменьшится в
				T	1
	Рис. 6. 8			е раз, то δ = βT = ---- =	---	. Таким обра-
				τ	N

зом, логарифмический декремент — безразмерная величина, обратная числу колебаний N, в течение которых амплитуда уменьшается в e раз.

Из выражения (6.10) следует, что при ω20 ≤ β2 колебания в сис-

теме не возникают. В этом случае наблюдается апериодический процесс (рис. 6.8), в результате которого вся запасенная в системе механическая энергия расходуется на работу против сил сопротивления. Каким из двух способов, показанных на рис. 6.8, система вернется в положение равновесия, зависит от начальных условий.

6.6. Вынужденные колебания. Резонанс

Вынуждающей силой называется переменная внешняя сила, приложенная к системе и вызывающая ее вынужденные механические колебания. Пусть вынуждающая сила изменяется по гармоническому закону F = F0 cos (ωt). Тогда дифференциальное уравнение вынуж-

денных колебаний запишем следующим образом:

d2x		dx	2	F0
--------		-----	+ ω0x =	-----	cos (ωt) .	(6.11)
dt	2	+ 2β dt		m

Общее решение этого уравнения имеет вид

x(t) = A0e– βtcos (ω′t + α) + A cos (ωt – ϕ0 ) ,

где ω′ = 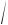ω20 – β20 . В этом выражении первое слагаемое играет роль

только на начальной стадии установления процесса колебаний. В дальнейшем этой составляющей решения можно пренебречь. Второе слагаемое описывает установившиеся вынужденные колебания (рис. 6.9).

84

		A(ω2	– ω2)
x	2βAω	0
Aω2		f0
t	ϕ0
		Aω2
			0
Рис. 6. 9	Рис. 6. 10

Подставим x(t) = A cos (ωt – ϕ0) в уравнение (6.11). Для этого найдем

·

(t) = –Aω sin (ωt – ϕ0 ) = Aω cos (ωt –

производные x(t) по времени: x

– ϕ0 + π ⁄ 2 )

··

2

cos (ωt – ϕ0 ) = Aω

2

cos (ωt – ϕ0 + π) .

и x(t) = –Aω

Тогда получим:

Aω2 cos (ωt – ϕ

0

+ π) + 2βAω cos (ωt – ϕ

0

+ π ⁄ 2) +

+ ω2A cos (ωt – ϕ

0

) = f

0

cos (ωt) ,

0

где f0 = F0 ⁄

m . Используя метод векторных диаграмм, представим

левую часть последнего уравнения в виде суммы трех векторов (рис. 6.10), модули которых указаны на рисунке. Результат сложения этих трех векторов — вектор, модуль которого равен f0. Из рис. 6.10

следует, что (при ω0 > ω)

	tg ϕ0		2βω
		=	--------------------		.
			ω2	– ω2
			0

По теореме Пифагора найдем амплитуду вынужденных колебаний:

		f0		(6.12)
A = ------------------------------------------------------------ .
	ω2	– ω2 2	+ 4β2ω2
	0

Из (6.12) следует, что при ω = 0 в системе происходит статическое смещение из положения равновесия под действием постоянной силы

F0 на величину f0/ω20 (рис. 6.11).

При неограниченном возрастании частоты внешнего воздействия (ω → ×)?амплитуда колебаний стремится к нулю, tg ϕ0 → 0 и ϕ0 → – π.

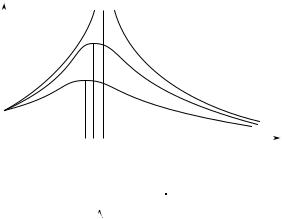
Дифференцируя выражение (6.12) по переменной ω и приравнивая полученную производную нулю, определяем такую частоту внешнего воздействия ω = ωp , при которой амплитуда колебаний

85

A			β1		β=0
f0
ω2				β	>β	1
0		ωp2	ω0	2
0			ωp1			ω

Рис. 6. 11

достигает максимума: ωp = 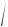ω20 – 2β2 . Явление резкого возраста-

ния амплитуды вынужденных колебаний при определенной частоте внешнего воздействия называется резонансом. График зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы при различных коэффициентах затухания системы приведен на рис. 6.11. Из формулы (6.12) следует, что

	Amax = A(ωp ) =	F0
		-----------------	.
		2mβωp

С явлением резонанса приходится считаться при конструировании машин и различных сооружений. Собственная частота колебаний этих устройств не должна быть близка к частоте возможных внешних воздействий, иначе может произойти разрушение конструкции. Вместе с тем явление резонанса часто оказывается весьма полезным, особенно в акустике, радиотехнике и т.д.

86

Г л а в а 7

ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ

Принцип относительности Галилея (см. § 2.1) утверждает эквивалентность всех инерциальных систем отсчета (ИСО) лишь для механических явлений. Поэтому этот принцип не может быть основой всей физической науки, так как выделяет механические явления как особые и, таким образом, не отражает материального единства различных физических явлений. Физическая теория, которая рассматривает пространственно-временные закономерности для любых физических процессов, называется теорией относительности. Она была создана А. Эйнштейном и в основном завершена к 1915 г. В основе этой теории лежит фундаментальный физический закон, согласно которому все законы физики (а не только законы механики) имеют одинаковую форму записи во всех ИСО. Теория относительности делится на две части: общую теорию относительности, изучающую неинерциальные системы отсчета и поля тяготения, и частную теорию относительности, изучающую ИСО в отсутствии полей тяготения. В современной литературе частную теорию относительности называют специальной теорией относительности (СТО) или релятивистской механикой. Основные выводы именно этой теории мы рассмотрим в нашем курсе.

Наши понятия о пространстве и времени сформировались из повседневного опыта, в котором мы имели дело с макротелами при не слишком больших скоростях. Явления же, рассматриваемые СТО, протекают в лабораторных экспериментах, и у нас нет навыка и опыта в их описании.

7.1. Инварианты преобразований Галилея

Объединив уравнения (1.17)—(1.19) в систему, можно получить преобразования Галилея при переходе от одной ИСО к другой:

º	º	′	º	t;
r	= r		+ v
t = t ′;
					(7.1)
º	º	′,
a	= a

º

где v — скорость одной ИСО относительно другой.

87

Зададимся вопросом: одинаково ли выполняются законы механики в этих ИСО? Для Галилея было очевидно, что m = m′ (масса тела не меняется при переходе от одной ИСО к другой). Проверим справедливость основного закона механики, т.е. второго закона

º

Ньютона (2.2). Пусть на тело в одной ИСО действует сила F , а в

другой — сила º′ . Все силы в механике делятся на потенциальные

F

(т.е. функции относительного положения тел) и непотенциальные (они зависят от скорости движения тел одного относительно другого). Исходя из первого уравнения системы (7.1), можно записать:

º		=	º			º
r	1			r	′ + v t;
				1
º		=		º		º		t,
r	2			r		′ +	v
				2
отсюда следует, что
		º		=		º	′ ,	(7.2)
		r				r

т.е. относительные расстояния между точками в разных ИСО одинаковы, если они измеряются в один момент времени. Это означает, что потенциальные силы, действующие на тело в различных ИСО, будут одинаковыми. Продифференцировав (7.2) по времени, получим

º = º′ , v v

т.е. непотенциальные силы, действующие на тело в различных ИСО, также будут одинаковыми. Поэтому для любых сил выполняется

равенство º = º′ . Именно поэтому в различных ИСО второй

F F

закон Ньютона имеет одинаковый вид (одинаковую форму записи):

º	º	º	º	′ .
m a	= F ;	m a	′ = F

Закон сохранения импульса также сохраняет свой вид при переходе от одной ИСО к другой.

Рассмотрим инварианты преобразований Галилея.

1. Длина отрезка.

В классической физике пространство обладает так называемой евклидовой метрикой. Это означает, что расстояние между двумя точками с координатами (x1, y1, z1) и (x2, y2, z2) определяется по тео-

реме Пифагора:

l = (x	1	– x	2	)2	+ (y	1	– y	2	)2	+ (z	1	– z	2	)2 .	(7.3)

Пусть две ИСО двигаются одна относительно другой вдоль оси ОХ.

88

Тогда преобразования Галилея (7.1) имеют вид:

x′ = x – vt;

y ′ = y;

z′ = z;

t′ = t.

Отсюда следует, что длина отрезка между данными точками во второй ИСО будет определяться по формуле

l′ = (x1′ – x2′ )2 + (y1′ – y2′ )2 + (z1′ – z2′ )2 = l .

Таким образом, длина отрезка, измеренная в неподвижной ИСО, равна длине того же отрезка, измеренной в движущейся ИСО, если измерения проводились в один момент времени.

2. Временной интервал.

Поскольку в классической физике время не меняется при переходе от одной ИСО к другой, то временной интервал между двумя событиями t = t1 – t2, измеренный в неподвижной ИСО, в точности

равен интервалу между этими событиями в движущейся ИСО:

t′ = t ′	– t ′	= t	1	– t	2	= t .
1	2

3. Изменение импульса и работа.

Поскольку радиус-вектор материальной точки, а следовательно,

иее скорость зависят от выбора начальных условий в различных ИСО, то они не являются инвариантами. Значит, импульс тела и его энергия не являются инвариантами. Рассмотрим изменение импульса

иизменение энергии.

Всоответствии со вторым законом Ньютона

º	º º	º	′ ,
d p	= F dt = F	′dt′ = d p

а это означает, что изменение импульса инвариантно.

Работа по перемещению тела равна изменению его кинетической энергии:

dA =	º	º	= d(mV	2	⁄ 2) .	(7.4)
	F d r

89

º

º

º

Записав

преобразования

Галилея

в

виде

′ + d R ,

d r = d r

º

º

º

, получим, что

V =

V ′ +

v

º

º

=

º

º

′

+

º º

.

(7.5)

F d

r

F d r

F d R

Воспользовавшись формулой (1.18), вычислим:

d

mV 2

m

º

′ +

º

2

m

d

º

′

2

º

º º2

=

------------

= d ----

V

v

= ----

V

+ 2 V ′ v

+ v

2

2

2

= d ----m

V

′

+ d m V ′ v

+ d

----m

v

2

=

º

2

º

º

º

2

2

m

º

2

+

º

º

+

º

º

+

m

º

º

= d ---- V

′

md V ′ v

m V

′d v

----

2 v

d v .

2

2

Поскольку

º

º

= 0 , а поэтому

v

= const , то d v

d

mV 2

=

m º

′2

º

º

=

d

m

º

º

º

) =

------------

d --- V

+ md V

′ v

---

V

′2 + (m a

′dt v

2

2

2

= d ---m V ′2

+

F

′d R .

(7.6)

º

º

º

2

Тогда, подставляя (7.5) и (7.6) в (7.4), получаем:

º º

+

º º

= d

m

º

2

+

º

º

,

F d r ′

F d R

---

V ′

F

′d R

2

отсюда следует, что

º

º

m

º

′2

, т.е. работа инвариантна.

F d r ′

= d ---

V

2

Данный вывод показывает справедливость одинаковой записи законов сохранения импульса и энергии в различных ИСО.

7.2.Постулаты Эйнштейна

В1860—1865 гг. английский ученый Д. Максвелл создал теорию электромагнитного поля и предсказал существование в свободном пространстве электромагнитного излучения (волн), которое распространяется со скоростью света. Это дало ему возможность предположить, что свет представляет собой один из видов электромагнитного излучения. В то время считалось, что электромагнитное излучение распространяется в особой невесомой среде (эфире), которая пронизывает все тела. Считалось, что с этим эфиром можно связать сис-

90