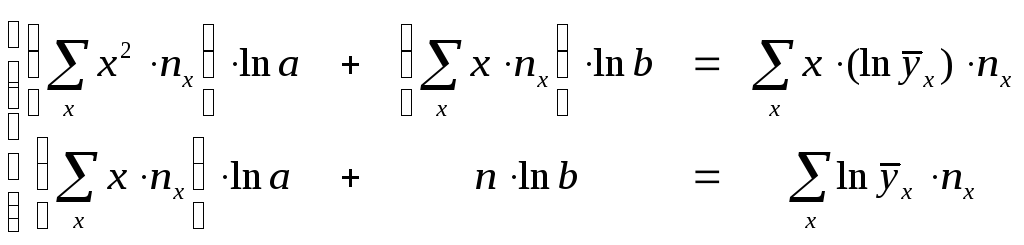2. Эмпирической линией регрессии у на х называется ломаная с вершинами в точках с координатами

.

Аналогично определяется эмпирическая линия регрессии у на х – ломаная с вершинами в точках с координатами

.

При этом и- групповые средние, которые определяются для каждого значенияx признака X в первом случае и для каждого значения y признака Y во втором. Их расчетные формулы таковы:

, .

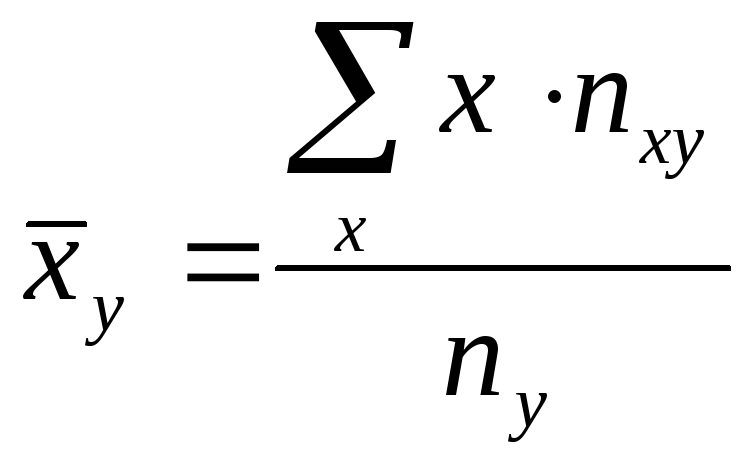3. Коэффициент линейной корреляции r позволяет определить форму корреляционной зависимости. Он подсчитывается по формуле:

.

Средние квадратические отклонения группировочных признаков определяются как арифметические квадратные корни из дисперсий. Дисперсии рассчитываются по определению или по формуле разностей (см. задачу 4), а также методом моментов (см. задачу 5). Величина μ может быть найдена двумя способами: по определению

,

,

а средние арифметические инаходятся по определению (задача 4) или методом моментов (задача 5); методом моментов (см. задачу 5)

.

В зависимости от r имеем следующую интерпретацию связи

Значение r	Интерпретация связи
	Линейная функциональная
	Линейная обратная
	Нелинейная
	Нелинейная
	Линейная прямая
	Отсутствует

4. Степень тесноты корреляционной связи устанавливается с помощью корреляционного отношения η, равного

,

При этом и- соответственно межгрупповое и общее средние квадратические отклонения, равные

, ,

.

Характер связи определяется так:

Значение η	Характер связи
	Отсутствует
	Практически отсутствует
	Слабая
	Умеренная
	Сильная
	Функциональная

Для проверки правильности произведенных вычислений удобно использовать свойство корреляционного отношения:

.

5. Проверить гипотезу о статистической значимости эмпирических данных, а следовательно о принципиальной возможности построения уравнения регрессионной модели можно с помощью t - критерия Стьюдента.

Правило проверки гипотезы. Если наблюдаемое значение критерия больше критического,

,

То это с вероятностью γ (уровнем значимости α = 1- γ) говорит о значимости коэффициента линейной корреляции, а следовательно о статистической значимости эмпирических данных. При этом

,

а критическое значение определяется по таблице (см. таблицу 3 Приложения):

, α = 1- γ, ν = n – 2.

6. Нахождение параметров уравнений линий регрессии у на х и х на у производится путем решения соответствующих систем нормальных уравнений. Для линейного случая существует еще один, упрощенный способ. Вид уравнений линейной, параболической и показательной регрессий и способы расчета их параметров помещены в таблицу 10.

7. Точность построенной регрессионной модели определяется с помощью средней ошибки аппроксимации , равной

,

при этом y и y* - соответственно эмпирическое и теоретическое (рассчитанное по модели) значение признака Y, соответствующее данному значению x признака X.

8. Степень влияния факторного признака X на результативный признак Y определяется с помощью индекса детерминации

.

9. Величины средней ошибки аппроксимации и индекса детерминации позволяют определить наиболее точную регрессионную модель. Ей считается та, у которой одновременно средняя ошибка аппроксимации стремится к минимуму, а индекс детерминации – к максимуму,

, .

10. Прогноз значения у происходит путем подстановки данного значения х в уравнение регрессии у на х. Аналогично, для прогноза значения х по заданному значению у, необходимо использовать уравнение регрессии х на у.

Таблица 10

	у на х	х на у
Линейная
	,	,
Параболическая
Показательная

Переходим к решению задачи. Вначале запишем исходные данные в виде корреляционной таблицы:

Х Y		(5;9)	(9;13)	(13;17)	(17;21)	(21;25)	(25;29)
		7	11	15	19	23	27
(1;3)	2					2	7	9
(3;5)	4				4	4	3	11
(5;7)	6			6	3	1		10
(7;9)	8		1	2	1			4
(9;11)	10		6	2				8
(11;13)	12	2	1					3
(13;15)	14	5						5
		7	8	10	8	7	10	50

Строим корреляционное поле данных (рисунок 10)

Рис. 10

Производим все необходимые вычисления в ниже приведенной таблице. В клетке, стоящей на пересечении строки и столбца указаны следующие данные:

X Y			(5;9)			(9;13)			(13;17)			(17;21)			(21;25)			(25;29)
			7			11			15			19			23			27
			-2			-1			0			1			2			3
(1;3)	2	-1													4		46	14		189	9	235	26,1111
																2			7
															92		-4	378		-21
(3;5)	4	0										16		76	16		92	12		81	11	249	22,6364
													4			4			3
												304		0	368		0	324		0
(5;7)	6	1							36		90	18		57	6		23				10	170	17
										6			3			1
									540		0	342		3	138		2
(7;9)	8	2				8		11	16		30	8		19							4	60	15
							1			2			1
						88		-2	240		0	152		2
(9;11)	10	3				60		66	20		30										8	96	12
							6			2
						660		-18	300		0
(11;13)	12	4	24		14	12		11													3	25	8,333
				2			1
			168		-16	132		-4
(13;15)	14	5	70		35																5	35	7
				5
			490		-50
			7			8			10			8			7			10			50
			94			80			72			42			26			26
			13,4286			10			7,2			5,25			3,7143			2,6			-
			658			880			1080			798			598			702			4716
			-66			-24			0			5			-2			-21			-108
			307,5657			81,92			1,6			19,22			66,6514			176,4			653,3571
			7			11			15			19			23			27
			7			8			10			8			7			10			50
			49			88			150			152			161			270			870
			343			968			2250			2888			3703			7290			17442
			2401			10648			33750			54782			85169			196830			383670
			16807			117128			506250			1042568			1958887			5314410			8956050
			94			80			72			42			26			26			340
			658			880			1080			798			598			702			4716
			4606			9680			16200			15162			13754			18954			78356
			2,5974			2,3026			1,9741			1,6582			1,3122			0,9555			-
			18,1817			18,4207			19,7408			13,2658			9,1853			9,5551			88,3494
			127,2718			202,6275			296,1122			252,0507			211,2620			257,9881			1347,3123

у
2	9	26,1111	18	36	72	144	235	470	940	3,2624	29,3612	58,7225
4	11	22,6364	44	186	704	2816	249	996	3984	3,1196	34,3151	137,2605
6	10	17	60	360	2160	12960	170	1020	6120	2,8332	28,3321	169,9928
8	4	15	32	256	2048	16384	60	480	3840	2,7081	10,8322	86,6576
10	8	12	80	800	8000	80000	96	960	9600	2,4849	19,8793	198,7925
12	3	8,333	36	432	5184	62208	25	300	3600	2,1203	6,3608	76,3295
14	5	7	70	980	13720	192080	35	490	6860	1,9459	9,7296	136,2137
	50	-	340	3040	31888	366592	870	4716	34944	-	138,8103	863,9692

Строим эмпирические линии (рисунок 11; на нем сплошной линией изображена эмпирическая линия регрессии у на х, а пунктирной – эмпирическая линия регрессии х на у) регрессии и делаем первоначальные выводы о форме корреляционной зависимости.

Рис. 11

Так как с ростом значения х значения у почти монотонно убывают, то скорее всего имеет место линейная обратная корреляционная зависимость.

Определим величину коэффициента линейной корреляции. Среднее значение признаков найдем согласно определению, а дисперсии рассчитаем по формуле разностей. Имеем:

;

;

;

;

;

;

;

.

Среднее значение произведения

.

Тогда числитель коэффициента линейной корреляции, рассчитанный первым способом, равен:

.

Найдем величину μ методом моментов. Используя соответствующие определения и расчетную таблицу, получаем:

.

Итак, коэффициент линейной корреляции равен:

,

что говорит о том, что рассматриваемая зависимость является линейной обратной.

Переходим к вычислению корреляционного отношения. Межгрупповая дисперсия равна

,

отсюда

;

.

Итак, корреляционное отношение равно

.

Найденное значение говорит о тесной корреляционной зависимости между рассматриваемыми признаками.

Проверим с вероятностью 0,95 гипотезу о статистической значимости эмпирических данных. Наблюдаемое значение критерия Стьюдента равно.

.

Критическое значение находим по таблице 3 приложения для уровня значимости α = 1- 0,95=0,05 и числа степеней свободы ν = 50 – 2= 48:

.

Имеем:

17,0664>2,02,

следовательно гипотеза о статистической значимости эмпирических данных принимается с указанной вероятностью.

Находим параметры регрессионных моделей (см. таблицу 10). Результаты вычислений представим в таблицах:

Линейная корреляционная зависимость
Система нормальных уравнений	у на х	Система
		Решение системы	,
		Уравнение
	х на у	Система
		Решение системы	,
		Уравнение
Упрощенный способ	у на х	ρ
		Уравнение	,
	х на у	ρ
		Уравнение	,

Параболическая корреляционная зависимость
у на х	Система
	Решение системы	, ,
	Уравнение
х на у	Система
	Решение системы	, ,
	Уравнение
Показательная корреляционная зависимость
у на х	Система
	Решение системы	, , ,
	Уравнение
х на у	Система
	Решение системы	, , ,
	Уравнение

По каждой из полученных моделей находим величину средней ошибки аппроксимации и индекса детерминации (расчеты приведены в таблице 11). Имеем: для линейной модели

, или 80,12%;

для параболической модели

, или 79,95%;

для показательной модели

, или 79,06%.

Видим, что одновременно минимум средней ошибки аппроксимации и максимум индекса детерминации соответствует линейной регрессионной модели. Следовательно, она признается наиболее точной.

Графики линейной зависимости приведены на рисунке 12, параболической – на рисунке 13, а показательной – на рисунке 14. На них сплошной чертой изображены линии регрессии у на х, а пунктирной – х на у.

Строим прогноз признаков. Имеем: при стоимости основных производственных фондов 2,5 млн. руб., затраты на капитальный ремонт составят

(%).

Если затраты на капитальный ремонт составляют 0,52% от ОПФ, то стоимость основных производственных фондов должна составлять

(млн. руб.)

Таблица 11

у				Линейная модель				Параболическая модель				Показательная модель
2	23	-4,8	23,04	3,8833	-1,8833	3,5469	0,9417	3,6100	-1,6100	2,5922	0,8050	3,6887	1,6887	2,8515	0,8443
	27	-4,8	23,04	1,8000	0,2000	0,0400	0,1000	2,6556	-0,6556	0,4298	0,3278	2,6524	0,6524	0,4256	0,3262
4	19	-2,8	7,84	5,9667	-1,9667	3,8678	0,4917	5,1586	-1,1586	1,3424	0,2897	5,1298	1,1298	1,2764	0,2824
	23	-2,8	7,84	3,8833	0,1167	0,0136	0,0292	3,6100	0,3900	0,1521	0,0975	3,6887	-0,3113	0,0969	0,0778
	27	-2,8	7,84	1,8000	2,2000	4,8400	0,5500	2,6556	1,3444	1,8074	0,3361	2,6524	-1,3476	1,8161	0,3369
6	15	-0,8	0,64	8,0500	-2,0500	4,2025	0,3417	7,3014	-1,3014	1,6935	0,2169	7,1340	1,1340	1,2859	0,1890
	19	-0,8	0,64	5,9667	0,0333	0,0011	0,0056	5,1586	0,8414	0,7079	0,1402	5,1298	-0,8702	0,7572	0,1450
	23	-0,8	0,64	3,8833	2,1167	4,4803	0,3528	3,6100	2,3900	5,7120	0,3983	3,6887	-2,3113	5,3423	0,3852
8	11	1,2	1,44	10,1333	-2,1333	4,5511	0,2667	10,0383	-2,0383	4,1545	0,2548	9,9212	1,9212	3,6911	0,2402
	15	1,2	1,44	8,0500	-0,0500	0,0025	0,0062	7,3014	0,6986	0,4881	0,0873	7,1340	-0,6660	0,7500	0,1083
	19	1,2	1,44	5,9667	2,0333	4,1344	0,2542	5,1586	2,8414	8,0735	0,3552	5,1298	-2,8702	8,2381	0,3588
10	11	3,2	10,24	10,1333	-0,1333	0,0178	0,0133	10,0383	-0,0383	0,0015	0,0038	9,9212	-0,0788	0,0062	0,0079
	15	3,2	10,24	8,0500	1,19500	3,8025	0,1960	7,3014	2,6986	7,2827	0,2699	7,1340	-2,8660	8,2140	0,2866
12	7	5,2	27,04	12,2167	-0,2167	0,0469	0,0181	13,3693	-1,3693	1,8751	0,1141	13,7974	1,7974	3,2307	0,1498
	11	5,2	27,04	10,1333	1,8667	3,4844	0,1556	10,0383	1,9617	3,8484	0,1635	9,9212	-2,0788	4,3213	0,1732
14	7	7,2	51,84	12,2167	1,7833	3,1803	0,1274	13,3693	0,6307	0,3977	0,0450	13,7974	0,2026	0,0410	0,0145
	-	-	202,24	-	-	40,2122	3,8489	-	-	40,5588	3,9051	-	-	-	3,9261

Рис. 12

Рис. 13

Рис. 14

Задача 10. Имеются следующие показатели по десяти предприятиям некоторой отрасли (на 31.12.2007):

Номер предприятия	Стоимость промышленно – производственных основных фондов, тыс. руб.	Валовая продукция в оптовых ценах предприятия, тыс. руб.	Среднесписочная численность промышленно – производственного персонала, чел.	Среднесписочная численность рабочих, чел.
1	4999	5349	420	331
2	6929	6882	553	486
3	6902	7046	570	498
4	10097	7248	883	789
5	8097	5256	433	359
6	11116	14090	839	724
7	4880	3525	933	821
8	7355	5431	526	428
9	10066	7680	676	607
10	7884	8226	684	619

Приняв стоимость основных промышленно – производственных основных фондов за результативный признак, а остальные показатели – за факторные признаки, необходимо:

а) исключив один из факторных признаков, перейти к двухфакторной регрессии;

б) вычислить множественный коэффициент корреляции и сделать выводы о форме и силе корреляционной зависимости;

в) с помощью F – критерия Фишера с вероятностью 0,95 оценить статистическую значимость эмпирических данных;

г) вычислить значение общего индекса детерминации;

д) двумя способами получить уравнение линейной модели множественной регрессии;

е) по величине средней ошибки аппроксимации оценить точность линейной модели;

ж) подсчитать дельта – коэффициенты;

з) найти значения коэффициентов эластичности;

и) исключить из модели один из факторных признаков и перейти к модели с парной регрессией.

1. Эмпирические данные выборки объема n принято записывать в виде таблицы, в которой Y – результативный признак со значениями , а,,…,- факторные признаки со значениями,i=1,2,…, n , j=1,2,…k:

	Y			…
1				…
2				…
n				…