Тема 6.3. Типы отношений

Теперь опишем несколько часто употребляемых типов отношений.

Часто приходится сталкиваться с отношениями, определяющими некоторый порядок расположения элементов множества.

Пример 6.6:отношения строгого порядка:

• отношения «быть больше», «быть меньше» на множестве действительных чисел;

• отношение строгого включения на множестве подмножеств данного множества;

• отношение «быть предком» на множестве людей.

Определение:Отношение строгого порядка– это антирефлексивное, несимметричное и транзитивное отношение на множестве .

Пример 6.7: отношения нестрогого порядка:

• отношение на множестве действительных чисел;

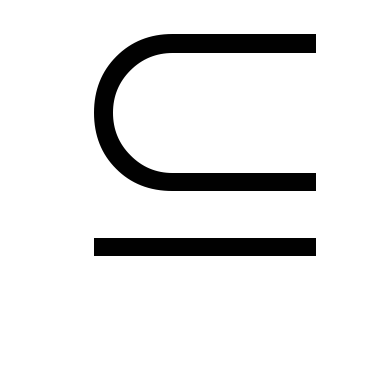• отношение на множестве подмножеств данного множества.

Определение:Отношение нестрогого порядка– это рефлексивное, антисимметричное и транзитивное отношение на множестве.

Некоторые элементы множества можно рассматривать как эквивалентные, если любой из этих элементов при некотором рассмотрении можно заменить другим.

Пример 6.8: отношения эквивалентности могут быть:

• отношение «быть синонимом» на множестве слов русского языка;

• отношение «иметь одинаковый остаток при делении на 3» на множестве целых чисел;

• отношение «быть параллельной» на множестве прямых одной плоскости;

• отношение «быть братом» на множестве людей.

Определение:Отношение эквивалентности– это рефлексивное, симметричное и транзитивное отношение на множестве.

Т.е. отношение эквивалентности удовлетворяет следующим условиям: каждый элемент эквивалентен сам себе, не важен порядок, в котором рассматриваются эквивалентные элементы, и если два элементы эквивалентны третьему, то они эквивалентны между собой.

Упражнение:Покажите, что все примеры отношения эквивалентности обладают перечисленными свойствами.

Определение:Пусть – некоторое отношение эквивалентности на множестве и пусть .Классом эквивалентности называется множество

Определение:Система называетсяпокрытием множества , если имеет место равенство

при этом называются блоками покрытия множества.

Определение:Система непустых подмножеств называетсяразбиением множества , если она является покрытием множества и .

Это понятие тесно связанно с отношением эквивалентности. Если рассматривать как множество, на котором введено отношение эквивалентности, то подмножество элементов, эквивалентных некоторому элементу из называетсяклассом эквивалентности. Если рассматривать на множестве студентов отношение «быть в одной группе», то группа, в которой учится студент Иванов, будет классом эквивалентности, эквивалентным студенту Иванову.

Из свойства транзитивности отношения эквивалентности следует, что все студенты, принадлежащие одному классу эквивалентности, эквивалентны между собой и всякий элемент из может находиться только в одном классе. Но в таком случае полная система классов эквивалентности является разбиением множества. Т.о. каждому отношения эквивалентности на множестве соответствует некоторое разбиение множества на классы. Эти понятия называют сопряженными.

Теорема:Пусть – некоторое отношение эквивалентности на множестве и . Тогда в том и только том случае, когда существует отношение .

Доказательство:Докажем что, , т.е. если элементы связаны отношением эквивалентности, то они принадлежат одному классу эквивалентности.

Рассмотрим , тогда по определению. Т.к. и- симметрично, то. В силу транзитивности изиследует. Поэтому, из чего следует, чтоАналогично доказывается иСледовательно.

Докажем обратное утверждение

и в силу рефлексивности отношения, что по определению означает.

Теорема:Пусть – некоторое отношение эквивалентности на непустом множестве . Семейство различных классов эквивалентности редставляет собой разбиение множества .

Определение:Системаназываетсяпродолжением разбиения, если.

Для разбиения множества справедливо правило суммы:

Для покрытия множества – обобщённое правило суммы:

Для подсчёта мощности множества , исходя из знания мощности его блоков покрытия, используется формула включения исключения, рассмотренная в разделе 3.

Теорема: Число различных разбиений множества мощности на блоков, где равно