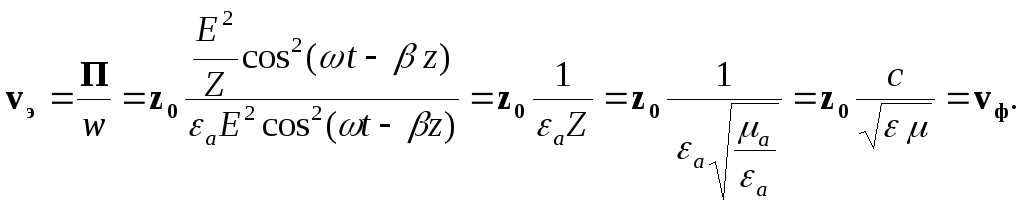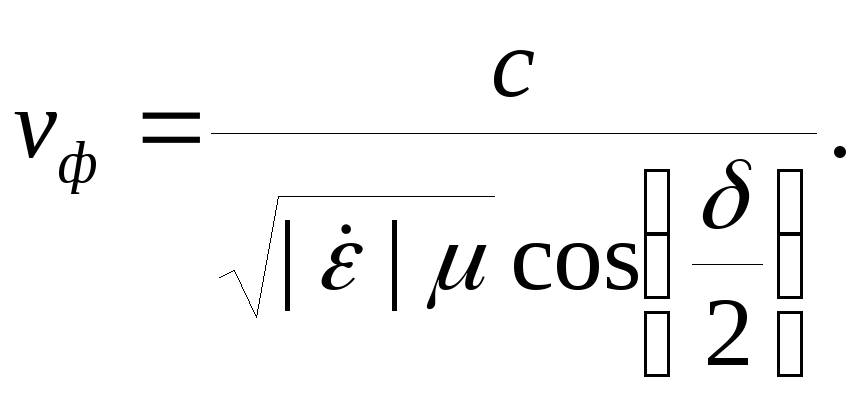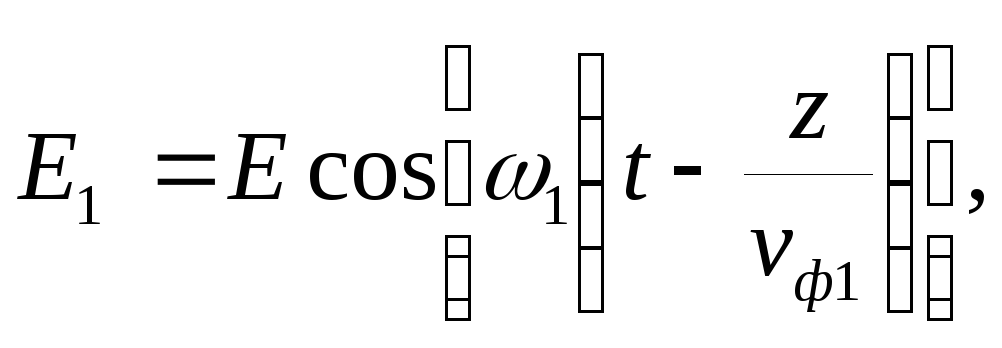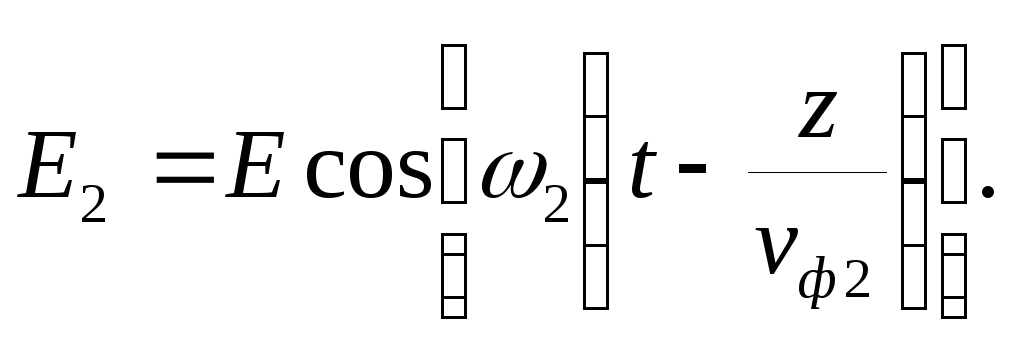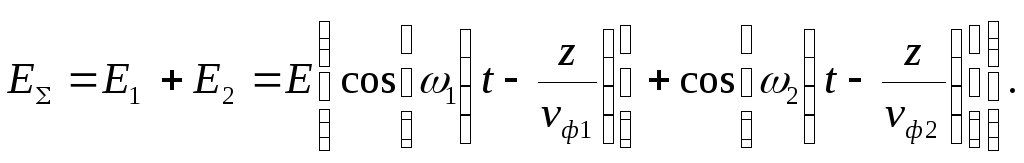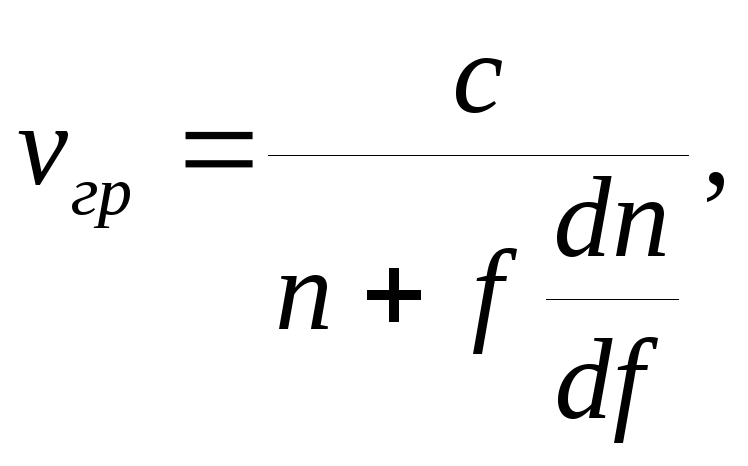7. Перенос энергии электромагнитной волной

Рассмотрим перенос энергии электромагнитной волной в однородной, линейной, изотропной среде без потерь. Перенос энергии электромагнитной волной описывается вектором Пойнтинга, который равен векторному произведению векторов напряженности электрического и магнитного полей:

(7.1)

Орт вектора Пойнтинга показывает направление переноса энергии, а модуль равен плотности ее потока.

Вычислить вектор Пойнтинга не трудно. Но нас интересует не плотность потока энергии, а скорость ее переноса. Скорость переноса энергии можно вычислить, разделив вектор Пойнтинга, то есть плотность потока энергии, на плотность энергии.

Плотность энергии электромагнитного поля складывается из двух составляющих - электрической и магнитной. Она описывается формулой:

(7.2)

где

w

- плотность энергии электромагнитного поля, Вт/м^3

Плотность энергии электрического поля равна скалярному произведению векторов напряженности электрического поля и электрической индукции, а плотность энергии магнитного поля – скалярному произведению векторов напряженности магнитного поля и магнитной индукции. Сумма этих составляющих и дает энергию электромагнитного поля.

Для вычисления вектора Пойнтинга и плотности энергии необходимо определиться с векторами поля. Пусть волна распространяется вдоль оси z, а вектор напряженности электрического поля направлен по осихи описывается следующим выражением:

(7.3)

В переменном электромагнитном поле в среде без потерь оба слагаемых плотности энергии равны между собой. Следовательно, плотность энергии можно описать такой формулой:

(7.4)

Эта формула получена следующим образом. Слагаемые равны, поэтому плотность энергии взята как удвоенное первое слагаемое формулы (7.2). Далее с помощью материального уравнения электрическая индукция заменена произведением напряженности электрического поля и абсолютной диэлектрической проницаемости, а затем выполнена операция умножения.

Осталось вычислить вектор Пойнтинга. Для этого не хватает вектора напряженности магнитного поля. Его можно найти с помощью волнового сопротивления среды. Получим:

(7.5)

В результате векторного умножения векторов напряженности электрического и магнитного поля получим вектор Пойнтинга:

(7.6)

Для того чтобы определить скорость переноса энергии надо плотность потока энергии разделить на плотность энергии. Получим:

(7.7)

Из формулы (7.7) следует важный вывод.

В среде без потерь и без частотной дисперсии скорость переноса энергии совпадает с фазовой скоростью

Волна в среде без потерь имеет еще одну особенность: векторы E и Н колеблются в фазе, вектор Пойнтинга является действительным и волна переносит только активную мощность.

Плоская электромагнитная волна в среде без потерь переносит только активную мощность

Однако среда без потерь – это идеальный случай. Как только появляются потери, возникает частотная дисперсия фазовой скорости. Это станет очевидно, если обратиться к формуле (5.15):

(5.15)

В явном виде частотная зависимость фазовой скорости в этой формуле не прослеживается. Но все-таки она есть. В формуле (5.15) используются модуль комплексной относительной диэлектрической проницаемости и угол потерь. Обе эти величины вычисляются через тангенс угла диэлектрических потерь, который и зависит от частоты.

Рассмотрим, как изменится скорость переноса энергии в среде с частотной дисперсией фазовой скорости. Проблема возникает из-за того, что монохроматическая волна не переносит информации, то есть не является сигналом. По определению, ее амплитуда постоянна, а время существования бесконечно. Характеристики поля изменяются во времени по заранее известному постоянному закону, и не могут переносить информацию.

Реальный электромагнитный процесс никогда не бывает одночастотным. Как только начинается излучение, волна перестает быть монохроматической. В ней, кроме колебания основной частоты, появляются и колебания других частот. Спектр сигнала еще более расширяется после прекращения излучения. На практике для передачи или извлечения информации чаще всего используются различные импульсы, а импульс любой формы и длительности характеризуются спектром частот. Значит, необходимо рассмотреть распространение не монохроматической волны.

Обратимся еще раз к формуле (7.7). Если ε и μ не зависят от частоты, то фазовая скорость и скорость переноса энергии любой спектральной компоненты сигнала одинаковы. В этом случае все компоненты волны приходят в точку приема одновременно, и сигнал на приеме сохранит свою форму.

Если нельзя не учитывать зависимость фазовой скорости волны от частоты, ситуация усложняется. В этом случае имеет место быть частотная дисперсияфазовой скорости.

При распространении сигнала в среде с дисперсией его спектральные составляющие распространяются с разной скоростью и достигают приемника не одновременно. Из-за этого форма сигнала искажается, причем на разных расстояниях фазовые соотношения между спектральными составляющими будут различны. Поэтому результаты сложения компонент сигнала будут зависеть от расстояния. Если эти искажения малы, ими можно пренебречь. Если нет – их необходимо учитывать.

Распространение не монохроматического сигнала в общем случае нельзя рассматривать как одну волну. Каждой спектральной составляющей будет соответствовать своя волна, распространяющаяся со своей фазовой скоростью. Для описания распространения не монохроматического сигнала в среде с частотной дисперсией фазовой скорости вводят понятие группы волн.

Группой волн называется не монохроматический волновой процесс при малой относительной ширине полосы сигнала

Можно полагать, что группа волн распространяется как одно целое. Однако скорость ее распространения отличается от фазовой и называется групповой скоростью.

Групповой называется скорость распространения группы волн

Насколько мала должна быть относительная ширина полосы сигнала и как поступать, если сигнал широкополосный, описано в литературе и не является предметом нашего курса. Мы же для первого ознакомления с проблемой рассмотрим распространение сигнала в не поглощающей среде с дисперсией фазовой скорости.

Для того чтобы определить групповую скорость, рассмотрим распространение двух электромагнитных волн одинаковой амплитуды и близких частот. Условие равенства амплитуд волн, составляющих группу, не является обязательным, но существенно упрощает выкладки. Мгновенные значения напряженности электрического поля этих волн можно описать следующими формулами:

	(7.8)
	(7.9)

Вид этих формул несколько необычен из-за того, что коэффициент фазы записан как отношение круговой частоты к фазовой скорости.

Для определения результирующего поля сложим эти волны. Получим:

(7.10)

Для дальнейших преобразований воспользуемся следующей формулой из тригонометрии:

(7.11)

Получим:

(7.12)

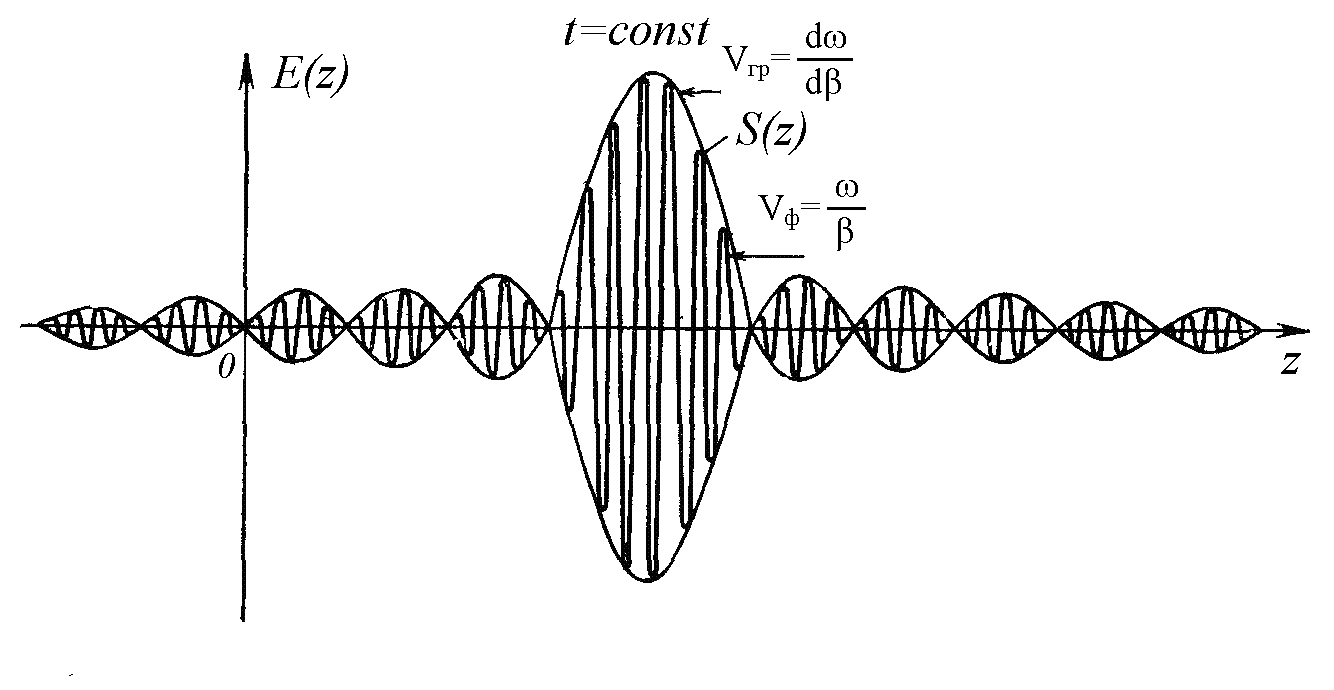
Формула (7.12) показывает, что сумма двух гармонических волн, содержит две составляющих принципиально разных частот. Так как частоты ω₁ и ω₂ близки, половина их разницы в первом сомножителе будет очень мала. А половина суммы во втором сомножителе будет равна средней частоте спектра сигнала. Значит, наш сигнал будет иметь высокочастотную несущую частоту и низкочастотную огибающую. Его мгновенный снимок приведен на рис. 7.1. Он очень похож на амплитудно модулированный сигнал.

Рис. 7.1. Мгновенный снимок сигнала, состоящего из двух гармонических составляющих

Огибающая сигнала описывается первым сомножителем формулы (7.12), а вы­сокочастотное заполнение - вторым. Максимум энергии сигнала совпадает с максимумом огибающей, так как именно в этом месте амплитуда волны максимальна.

Групповую скорость радиоволны определяют как скорость перемещения огибающей в предположении, что разница частот стремится к нулю. Не вдаваясь в подробности вывода, приведем конечную формулу:

(7.13)

где

- показатель преломления.

Групповая скорость является скоростью переноса энергии в среде с частотной дисперсией

Понятие групповой скорости оказывается полезным до тех пор, пока дисперсия еще не приводит к существенному искажению сигнала.