3. Решение волновых уравнений

Так как процесс создания электромагнитных волн нас пока не интересует, рассмотрим гармонические колебания в области, не содержащей источников. Для его описания необходимо решить уравнения (2.30) и (2.31). В такой записи вид уравнений не зависит от системы координат, в которой их необходимо решать. От системы координат зависит только оператора Лапласа.

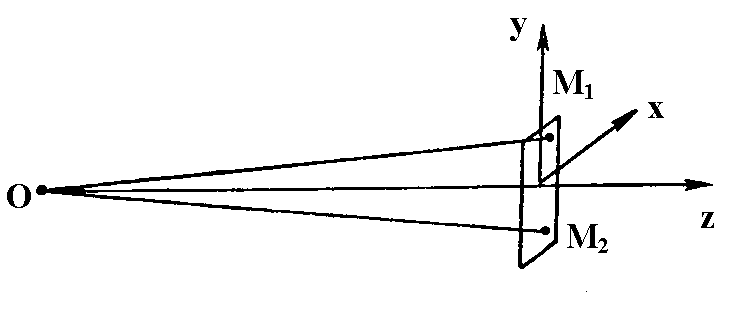
Найдем простейшее решение волновых уравнений в декартовой системе координат и выясним их физическое содержание. Для этого проанализируем параметры электромагнитной волны от точечного источника, находящегося в точке 0 (рис. 3.1). Через источник и исследуемую область проведена ось z. Распространение электромагнитной волны вдоль этой оси мы и должны описать.

Рис. 3.1. Решение волновых уравнений в декартовой системе координат

Для этого рассмотрим площадку, перпендикулярную осиz. Будем полагать, что площадка расположена очень далеко от источника, так далеко, что любые две ее точки можно считать находящимися на одинаковых расстояниях. Пусть это будут точки М₁и М₂на рис. Рассмотрим отрезки 0М₁и 0М₂, соединяющие выбранные точки площадки с источником. В пределах принятого допущения они равны и параллельны. Это значит, что точки М₁и М₂по отношению к источнику совершенно равноправны. Следовательно, при переходе от точки М₁к точке М₂ мы не заметим изменений характеристик электромагнитного поля.

Характеристики волны на площадке не зависят от поперечных координат х и у, значит, частные производные векторов поля по этим координатам равны нулю. Отсюда вытекает упрощение оператора Лапласа. В его составе останется только вторая производная по продольной координате z:

(3.1)

Естественно, упрощаются и волновые уравнения. Так, уравнение (2.31) примет вид:

(3.2)

Это уравнение выбрано для примера: уравнение (2.30) решается точно так же и для понимания способа описания характеристик поля достаточно решить любое из однородных волновых уравнений для комплексных амплитуд.

Решение уравнения (3.2) известно. Дело в том, что математические формулировки большинства задач электродинамики не являются уникальными. Макроскопическая электродинамика сложилась только во второй половине 19 века. К тому времени уже было сформулировано и решено значительное количество волновых задач из других областей науки, в частотности, из механики. Поэтому при решении задач электродинамики часто достаточно преобразовать уравнение к виду, решение которого уже известно.

К этому же классу задач относится и дифференциальное уравнение (3.2). Его общее решение описывается формулой:

(3.3)

где	h0	- орт, указывающий ориентацию вектора напряженности магнитного поля в пространстве;
	А, В	- произвольные коэффициенты, имеющие размерность напряженности магнитного поля, А/м;

Входящее в них комплексное волновое число используется для описания изменения амплитуды и фазы волны при распространении. Оно состоит из действительной и мнимой части:

(3.4)

где	β	- коэффициент фазы, рад/м;
	α	- коэффициент затухания, 1/м.

Изменение фазы при распространении описывает произведение βz, а амплитуда убывает по экспоненциальному закону: exp(-αz) Действительное волновое число соответствует среде без потерь и равно коэффициенту фазы.

Формула (3.3) описывает электромагнитную волну, распространяющуюся вдоль оси z. При постановке задачи мы потребовали, чтобы на плоскости, перпендикулярной осиz, характеристики поля не зависели от поперечных координат х и у. А что такое характеристики поля в данном случае? Это амплитуда напряженности поля и фаза волны. Значит, фаза волны постоянна на плоскости и волна являетсяплоской. В математическом описании волны о том, что она плоская, говорит зависимость фазы, то есть показателя степени экспонент, от единственной координатыz.

Кроме фазы, на плоскости фронта не изменяется и амплитуда напряженности поля. Это ее свойство мы также оговорили в условии задачи. Следовательно, волна, является однородной.

В формулу (3.3) расстояние входит только в мнимый показатель степени экспоненты. Это означает, что при распространении в среде без потерь с расстоянием изменяется только фаза волны, а амплитуда постоянна.

Амплитуда плоской волны в среде без потерь не зависит от расстояния

Решение (3.3) является общим, то есть оно описывает все возможные процессы, удовлетворяющие уравнению (3.2). Это решение состоит из двух слагаемых. Первое слагаемое описывает волну, распространяющуюся в положительном направлении оси z. Это понятно из следующих рассуждений. Фаза в месте расположения источника поля, при z = 0, описывается произведением ωt. Если z > 0, зависимость фазы волны от расстояния и координаты z описывается разностью ωt – βz. β – это действительная часть волнового числа, положительная по определению. Поэтому у волны, распространяющейся в положительном направлении оси z, отставание фазы пропорционально расстоянию. Следовательно, первое слагаемое в фигурных скобках описывает волну, удаляющуюся от источника. Это и было оговорено при формулировке задачи.

Во втором слагаемом перед произведением волнового числа на расстояние стоит знак плюс. Следовательно, чем дальше от источника, тем на больший угол фаза волны опережает фазу источника. Но эта ситуация не соответствует формулировке задачи. Значит, амплитудный коэффициент перед вторым слагаемым должен быть равен нулю и решение уравнения (3.2) примет вид:

(3.5)

Для получения частного решения осталось определить коэффициент А. Это амплитуда вектора напряженности магнитного поля. Обычно она находится из начальных условий, граничных условий или как-нибудь иначе. Но мы этого делать не будем. При выводе уравнений (2.30) и (2.31) мы условились, что среда, в которой распространяется электромагнитное поле, является линейной, то есть ее свойства не зависят от амплитуды напряженности поля. Поэтому для описания распространения электромагнитных волн величина амплитуды напряженности магнитного поля нам не нужна и решение (3.5) примет вид:

(3.6)

где

Н0

- любая действительная амплитуда вектора напряженности магнитного поля, А/м.

Уравнение (2.30) для вектора напряженности электрического поля решается так же, и вид решения будет таким же, кроме обозначения вектора поля и его орта:

(3.7)

где	е0	- орт вектора напряженности электрического поля;
	Е0	- действительная амплитуда вектора напряженности электрического поля, В/м.

Мы получили решение волновых уравнений в декартовой системе координат, у которой все три координатные поверхности – плоскости. Это наиболее простой, но весьма важный случай. И о плоской волне мы чаще всего будем говорить далее.

Однако для описания всех случаев, встречающихся в практической радиотехнике одного приближения плоской волны недостаточно. Поэтому коротко рассмотрим еще два решения – цилиндрические и сферические волны.

Очевидно, что описывать цилиндрические и сферические волны надо в цилиндрической и сферической системах координат соответственно. Ход решения этих задач аналогичен описанному выше, но более сложен из-за более сложного представления оператора Лапласа. Поэтому сразу приступим к описанию цилиндрической и сферической волн. Необходимо иметь ввиду, что эти волны также являются однородными, то есть амплитуда на поверхности волнового фронта постоянна.

Цилиндрические волны - это волны, имеющие осевую симметрию. Они могут возбуждаться, например, бесконечной прямой нитью источников. Фронты волны при этом имеют вид концентрических круговых цилиндров.

Пусть источники расположены вдоль оси zцилиндрической системы координат. Доказано, что в этом случае на расстоянии, значительно превышающем длину волны, комплексная амплитуда вектора напряженности электрического поля будет убывать пропорционально корню квадратному из расстояния:

(3.10)

где

r

- расстояние в цилиндрической системе координат, м.

Обратите внимание на то, что в эту формулу расстояние входит не только в мнимый показатель степени экспоненты, но и стоит под корнем в знаменателе.

Амплитуда цилиндрической волны в среде без потерь обратно пропорциональна корню квадратному из расстояния

Это убывание происходит по следующей причине. Плотность энергии электромагнитной волны пропорциональна квадрату амплитуды вектора напряженности поля. Волна однородная, поэтому плотность энергии одинакова во всех точках фронта. В цилиндрической волне площадь фронта волны S(поверхности цилиндра) пропорциональна расстоянию до его осиr. Она вычисляется как произведение длины окружности сечения цилиндра 2πrна его высотуh:S= 2πrh. Следовательно, плотность энергии на фронте волны будет изменяться обратно пропорционально радиусу цилиндра, а напряженность электромагнитного поля – пропорционально корню из этого расстояния.

Сферические волны возникают, например, тогда, когда очень маленький источник возбуждает неограниченное однородное пространство. Зависимость комплексной амплитуды сферической волны от расстояния описывается формулой:

(3.11)

где

r

- расстояние в сферической системе координат, м.

Из этой формулы видно, что амплитуда колебаний в сферической волне обратно пропорциональна расстоянию.

Амплитуда сферической волны в среде без потерь обратно пропорциональна расстоянию

Причина такого закона уменьшения напряженности поля такая же, как и у цилиндрической волны. Но площадь фронта увеличивается быстрее, пропорционально квадрату расстояния: S = 4πr². Значит, плотность энергии обратно пропорциональна квадрату расстояния, а напряженность поля – расстоянию в первой степени.

Этим же объясняется и отсутствие зависимости амплитуды напряженности поля от расстояния у плоской волны: площадь ее фронта не зависит от пути, пройденного волной.