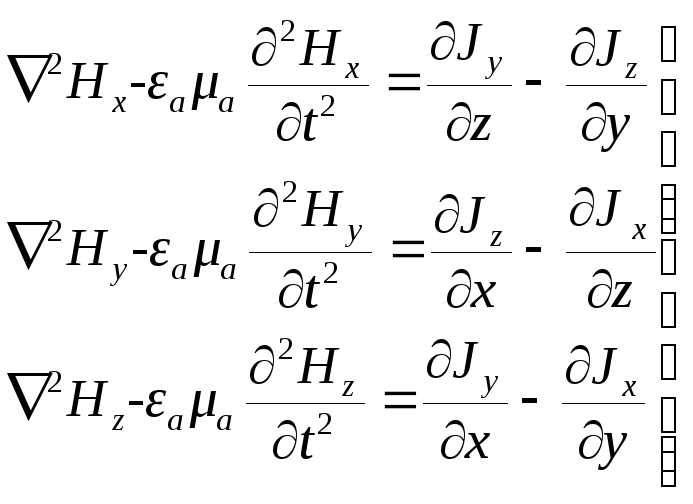2. Волновые уравнения

Большинство задач электродинамики, в том числе и описание распространения радиоволн, может быть решено с помощью системы уравнений Максвелла в дифференциальной форме:

	(2.1)
	(2.2)
	(2.3)
	(2.4)

где	Н	- вектор напряженности магнитного поля, А/м,
	J	- вектор плотности тока, А/м^2,
	D	- вектор электрической индукции, Кл/м^2;
	Е	- вектор напряженности электрического поля, В/м,
	В	- вектор магнитной индукции, Т,
	ρ	- объемная плотность электрических зарядов, Кл/м^3.

Эту систему необходимо решать совместно с материальными уравнениями, учитывающими взаимодействие электромагнитного поля со средой:

	(2.5)
	(2.6)
	(2.7)

где	εа	- абсолютная диэлектрическая проницаемость среды, Ф/м,
	μа	- абсолютная магнитная проницаемость среды, Гн/м,
	Jпр	- вектор плотности тока проводимости, А/м^2,
	σ	- электропроводность среды, См/м.

В общем случае точное решение этой системы встречает значительные трудности, поэтому ее необходимо преобразовать к более удобному виду, введя упрощающие предположения. Будем считать, что среда распространения электромагнитных волн является линейной, изотропной и однородной.

Линейной называется среда, свойства которой не зависят от амплитуд векторов электромагнитного поля

Изотропной называется среда, свойства которой не зависят от направления распространения волны

Однородной называется среда, свойства которой не зависят от координат

Как правило, типичные среды распространения электромагнитных волн являются линейными и изотропными. Однородные среды встречаются значительно реже.

Нашей ближайшей задачей является получение и решение двух уравнений, каждое из которых будет содержать только один неизвестный вектор напряженности поля, электрического Е или магнитного Н.

Начнем с уравнения, описывающего вектор напряженности магнитного поля. Для его вывода возьмем первое уравнение Максвелла (2.1) и с помощью материального уравнения (2.5) заменим в нем вектор электрической индукции произведением абсолютной диэлектрической проницаемости и вектора напряженности электрического поля. Получим:

(2.8)

Далее применим к этому уравнению оператор rot и изменим порядок дифференцирования по времени и координатам. Получим:

(2.9)

Левую часть уравнения (2.9) надо преобразовать с помощью известно­го тождества векторного анализа, которое применительно к нашей задаче примет вид:

(2.10)

где

- оператор Лапласа.

Оператор div, стоящий в правой части равенства (2.10), характеризует наличие источников поля в интересующей нас точке пространства. Так как силовые линии магнитного поля непрерывны, источников они не имеют и дивергенция вектора напряженности магнитного поля всегда равна нулю:divH = 0. С учетом этого равенство (2.10) примет вид:

(2.11)

Подставим это равенство в уравнение (2.9). Получим:

(2.12)

Далее надо обратиться ко второму уравнению Максвелла (2.2) и с помощью материального уравнения (2.6) заменить в нем вектор магнитной индукции вектором напряженности магнитного поля. Получим:

(2.13)

Это соотношение позволяет исключить вектор напряженности электрического поля из уравнения (2.12). Получим:

(2.14)

Цель достигнута. Мы вывели уравнение, в которое входит только неизвестный вектор напряженности магнитного поля. Это векторное уравнение эквивалентно трем скалярным уравнениям. В декартовой системе они имеют вид:

(2.15)

Уравнение (2.14) можно аналогичным образом расписать в цилиндрической и в сферической системах координат. При необходимости соответствующие формулы можно найти в литературе или вывести самостоятельно.

Уравнения такого вида описывают волновые процессы и называются неоднородными уравнения­ми Даламбера, или неоднородными волновыми уравнениями.

Однако классическое волновое уравнение выглядит несколько иначе. Например, в декартовой системе координат оно имеет вид:

(2.16)

где

vф

- фазовая скорость, м/с.

Сравнение уравнений (2.15) и (2.16) позволяет утверждать, что множитель, стоящий перед производной от составляющей вектора напряженности магнитного поля по времени также обратно пропорционален квадрату фазовой скорости:

(2.17)

где

vф

- фазовая скорость электромагнитной волны, м/с.

Теперь необходимо вспомнить, что абсолютная диэлектрическая проницаемость может быть представлена в виде произведения относительной диэлектрической проницаемости и электрической постоянной: ε_а = εε₀. Аналогично можно представить и абсолютную магнитную проницаемость μ_а: μ_а = μμ₀. С учетом этого формулу (2.17) можно переписать в более удобном виде:

(2.18)

Электрическая и магнитная постоянные – это числа. Разберемся, что получится в результате деления единицы на корень квадратный из их произведения:

(2.19)

где

с

- скорость света в вакууме, с ≈ 3*10^8 м/с.

Следовательно, фазовую скорость электромагнитной волны в среде можно описать формулой:

(2.20)

Формула (2.20) показывает, что любое отличие характеристик среды от вакуума приводит к уменьшению фазовой скорости электромагнитных волн.

Таким образом, уравнение (2.14) примет вид:

(2.21)

Уравнение (2.21) получено из системы уравнений Максвелла и позволяет рассчитать напряженность магнитного поля. Подобное уравнение можно вывести и для вектора напряженности электрического поля. Надо взять второе уравнение Максвелла (2.2), применить к нему оператор rot и проделать преобразования, аналогичные выполненным выше. Получим:

(2.22)

Если правая часть уравнений (2.21) и (2.22) будет равна нулю, получатся однородные уравнения Даламбера или однородные волно­вые уравнения.

В правых частях уравнений (2.21) и (2.22) стоят все токи, протекающие в интересующем нас объеме, за исключением токов смещения. Токи смещения учтены вторым слагаемым в левой части уравнения (2.22): их величина пропорциональна скорости изменения электрического поля. Следовательно, ток J включает в себя ток проводимости J_пр и сторонний ток J_ст, если они имеются в исследуемой области пространства. Учтем этот факт в уравнениях (2.21) и (2.22). Получим:

	(2.23)
	(2.24)

где	Jпр	- вектор плотности тока проводимости, А/м^2.
	Jст	- вектор плотности стороннего тока, А/м^2.

Сторонний ток J_ст обычно полагается известным, а ток проводимости J_пр создается рассчитываемым полем. Поэтому правые части уравнений надо преобразовать так, чтобы там остался только сторонний ток. Для этого надо:

• используя материальное уравнение (2.7), представить вектор плотности токов проводимости J_пр как произведение электропроводности σ на вектор напряженности электрического поля Е: J_пр = σЕ;

• подставить это выражение в уравнения (2.23) и (2.24);

• перенести произведение σ(дЕ/дt) в левую часть уравнения (2.23);

• rotE в правой части уравнения (2.24) заменить с помощью уравнения (2.13) и произведение μ_аσ(дН/дt) перенести в левую часть.

Получим:

	(2.25)
	(2.26)

В левых частях уравнений (2.25) и (2.26) находятся векторы Е и Н искомого поля, а в правых – векторы плотности сторонних токов, это поле создающих. Это – наиболее общий вид волновых уравнений электродинамики.

Для описания монохроматического поля необходимо преобразовать уравнения (2.25) и (2.26) с учетом следующих особенностей метода комплексных амплитуд:

• векторы Е, Н и J_ст заменить их комплексными аналогами;

• первая производная любого вектора по времени для комплексного аналога эквивалентна умножению его jω;

• вторая производная любого вектора по времени эквивалентна умножению его –ω²;

• электрические потери, представленные в уравнениях (2.25) и (2.26) электропроводностью σ, учитываются введением комплексной абсолютной диэлектрической проницаемости:

(2.27)

• магнитными потерями пренебрегаем.

В результате этих преобразований получим:

	(2.28)
	(2.29)

где

- комплексное волновое число.

Уравнения такого вида называют неоднородными уравнениями Гельмгольца или неоднородными волновыми уравнениями для комплексных амплитуд.

Если в интересующей нас области пространства сто­ронние источники отсутствуют, то есть J_cт = 0, то уравнения (2.28) и (2.29) уп­рощаются:

	(2.30)
	(2.31)

Такие уравнения называются однородными урав­нениями Гельмгольца или однородными волновыми уравнениями для комплексных амплитуд.

Их и необходимо решать для того, чтобы описать монохроматическую электромагнитную волну в области без источников.