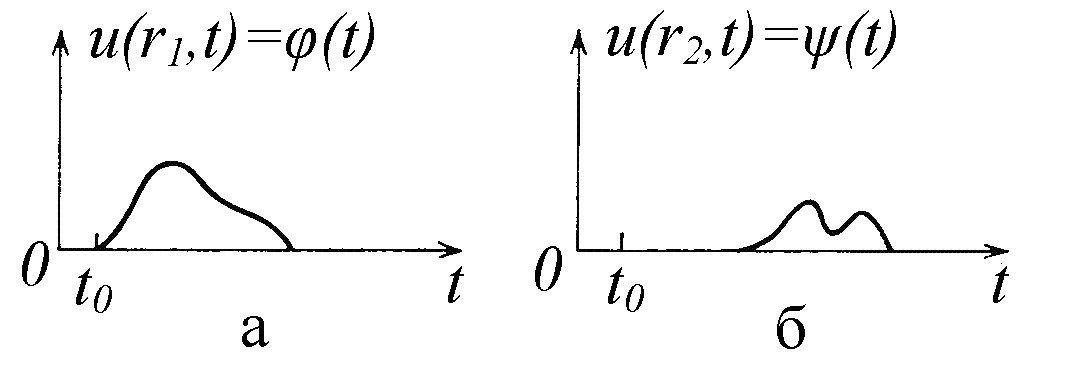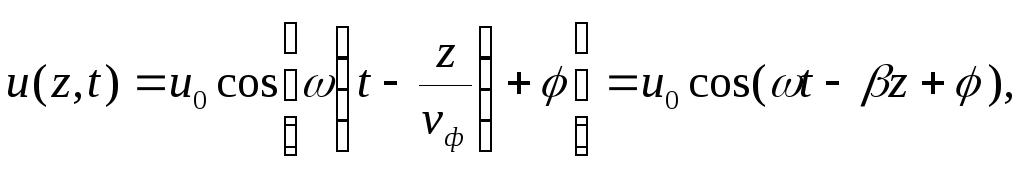1. Общие свойства волновых процессов

Рис. 1.1. Распространение волны во времени

Математическое описание волнового процесса базируется на простых и очевидных соображениях. Пусть в точке А с координатой r₁ физический процесс описывается функцией u(r₁, t) = φ(t), график которой приведен на рис. 1.1, а. Процесс в точке А начинается в момент времени t₀. Теперь рассмотрим точку Б, находящуюся на расстоянии l от точки А. Этой точке соответствует координата r₂. Наш физический процесс не будет наблюдаться в этой точке до тех пор, пока он не будет передан средой.

Через некоторое время мы получим в точке Б процесс, описываемый функцией u(r₂, t) = ψ(t). Зависимость функции u в точке Б от времени приведена на рис. 1.1, б. В общем случен она отличается от зависимости в точке А из-за затухания, искажения при распространении, влияния помех и т.д. Но в простейшем случае в точке Б мы обнаружим лишь запаздывание по времени того процесса, что происходил в точке А. При этом будет выполняться следующее очевидное равенство:

(1.1)

где

τ

- время прохождения пути l между точками А и Б, с.

Аргумент функции φ называется фазой волны, а величина τ являетсясдвигом фазыволны на пути между точками А и Б.

Пусть волна распространяется вдоль оси z. Тогда ее можно описать функцией:

(1.2)

где

v

- скорость распространения волны, м/с.

Таким образом, в простейшем случае волна в точках А и Б отличается только сдвигом фазы. Для конкретизации описания процесса распространения волны вводится понятие фронта волны.

Фронтом волны называется поверхность постоянной фазы

Распространение волны можно изучать как перемещение ее фронта. Для этого обратимся еще раз к формуле (1.2) и зафиксируем время. Фаза волны – это аргумент функции φ. Волна распространяется вдоль оси z и ее фаза не зависит от координат х и у. Значит, поверхность, на которой фаза постоянна (фронт волны) будет плоскостью, перпендикулярной оси z, вдоль которой распространяется волна. Поэтому волна, распространение которой описывается формулой (1.2), называется плоской.

Плоской называется волна, фронт которой имеет форму плоскости

Эта волна имеет еще одно важное свойство. Амплитуда волны не зависит от поперечных координат х и у. Следовательно, она одинакова во всех точках поверхности фронта волны и волна является однородной.

Однородной называется волна, амплитуда которой постоянна на поверхности фронта волны

Рассмотрим процесс распространения волны, изображенный на рис. 1.2. В разные моменты волна будет находиться в разных точках оси z. Зафиксируем некоторое мгновенное значение сигнала. На рис. 1.2 она обозначена буквой а. Этой величине сигнала в момент времени t₁ соответствует координата z₁. За время τ = t₂ – t₁ выбранная нами точка со скоростью v переместится на расстояние l = vτ. Кривые для моментов t₁ и t₂ на рис. 1.1 называют мгновенными снимками волны.

Рис. 1.2. Распространение волны вдоль оси z

Мгновенным снимком называется пространственное распределение волны в фиксированный момент времени

Плоская волна может распространяться не только в положительном, но и в отрицательном направлении оси z. Для описания волны, распространяющейся в отрицательном направлении, нужно изменить знак скорости v, то есть в формуле (1.2) изменить аргумент t - z/v на t + z/v.

Как правило, при описании колебаний в электродинамике используются гармонические функции sin и cos.

Гармоническими функциями называются sin и cos

Эти функции являются монохроматическими, то есть одночастотными.

Монохроматическим называется колебание одной частоты

Использование этих простейших периодических функций декартовой системы координат обусловлено тем, что реальные процессы весьма сложны. Поэтому для упрощения анализа их раскладывают на монохроматические составляющие с помощью рядов или интегралов Фурье. Затем распространение каждой составляющей спектра сигнала анализируют отдельно.

Гармонические функции являются периодическими.

Периодической называется функция, значения которой повторяются через равные промежутки

Если периодическая функция зависит от времени, ее значения повторяются через промежуток времени, кратный периоду.

Периодом называется минимальный промежуток времени, через который значения периодической функции повторяются

Период гармонической функции связан с частотой колебаний следующим соотношением:

(1.3)

где	Т	- период, с,
	f	- частота, Гц.

Если периодической функцией описывается волна, то вводится также и пространственный период. Он называется длиной волны.

Длиной волны называется расстояние, через которое значения периодической функции повторяются

Очевидно еще и следующее определение длины волны.

Длиной волны называется расстояние, проходимое волной за период

Следовательно, для вычисления длины волны необходимо скорость ее распространения умножить на период или разделить на частоту:

(1.4)

где

vф

- фазовая скорость волны, м/с.

Фазовой скоростью называется скорость перемещения фронта волны

Необходимо помнить, что пространственный и временной периоды подобны: за любой из них фаза волны изменяется на 2π.

Для гармонической волны формула (1.2) примет следующий вид:

(1.5)

где	u0	- амплитуда волны;
	ω	- круговая частота, рад/с;
	φ	- начальная фаза волны, рад;
	β	- коэффициент фазы, рад/м.

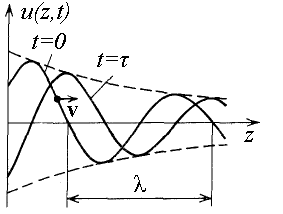
Рис. 1.3. Мгновенные снимки бегущей волны в среде без потерь

Эта формула описывает мгновенное значение волны в момент времени t на расстоянии z от источника. Аргумент косинуса называется фазой волны, а введенный здесь параметр β = ω/v – коэффициентом фазы.

Коэффициент фазы показывает, на сколько радиан изменится фаза волны при прохождении одного метра пути

На рис. 1.3 приведены мгновенные снимки бегущей гармонической волны в среде без потерь. Графики построены для двух фиксированных моментов времени 0 и τ. Потерь в среде нет, поэтому амплитуда волны не уменьшается по мере перемещения вдоль оси z. Оба графика - это синусоиды, сдвинутые на расстояние l, которое волна проходит за время τ.

Так как графики построены в зависимости от расстояния, можно выделить пространственный период волны, то есть ее длину λ. Видно, что на пути в одну длину волны фаза изменяется на 2π. Так как волновое число показывает, на сколько радиан изменяется фаза воны на пути в 1 метр, будет выполняться следующее равенство: βλ = 2π. Следовательно, коэффициент фазы можно вычислить двумя способами:

(1.6)

Из этого соотношения легко определить фазовую скорость. Получим:

(1.7)

Распространение гармонической бегущей волны отображается на рисунках смещением синусоиды со скоростью v_ф.

Рассмотрим две гармонические волны одинаковой частоты, распространяющиеся навстречу друг другу. Математически этот процесс можно описать следующим образом:

(1.8)

где		- амплитуда волны, распространяющейся в положительном направлении оси z;
	φ	- начальная фаза этой волны;
		- амплитуда волны, распространяющейся в отрицательном направлении оси z;
	ψ	- начальная фаза этой волны;

Такой вариант распространения встречается, например, при падении плоской волны на абсолютно отражающую плоскость по направлению нормали.

Прямая и обратная волны складываются и образуют поле достаточно сложной структуры. В простейшем случае, когда амплитуды и начальные фазы волн равны, результирующее поле будет описывать следующее соотношение:

(1.9)

Формула (1.9) описывает стоячую волну. Первый косинус формулы (1.9) описывает изменение величины волны во времени, второй – в пространстве, вдоль оси z. Из этой формулы видно, что нули и максимумы стоячей волны неподвижны. Нули стоячей волны называются узлами, а максимумы – пучностями.

Узлами стоячей электромагнитной волны называются точки, в которых амплитуда волны всегда равна нулю

Пучностями стоячей электромагнитной волны называются точки, в которых амплитуда достигает максимальных значений

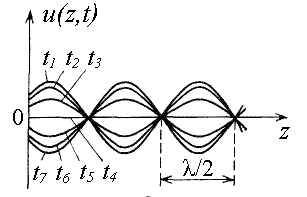
Рис. 1.4. Мгновенные снимки стоячей волны

Стоячей называется волна, узлы и пучности которой неподвижны

Семь мгновенных снимков стоячей волны приведено на рис. 1.4. В первой полуволне, на которой обозначены моменты времени, величина волны максимальна при t = t₁, равна нулю при t = t₄, а минимальна при t = t₇. В следующей полуволне волна максимальна при t = t₇, равна нулю при t = t₄, а минимальна при t = t₁. И так далее. Распределение величины волны повторяется с шагом в один период.

Все сказанное выше о волнах относится к средам без потерь. Но такие среды практически не встречаются. Некоторые потери энергии при распространении любой волны есть всегда. Значит, амплитуда волны должна уменьшаться с расстоянием и это уменьшение необходимо как-то описать. Проще всего это сделать с помощью метода комплексных амплитуд.

Методом комплексных амплитудназывается проведение расчетов с использованием комплексного представления гармонических величин

Комплексный аналог формулы (1.5), описывающей плоскую бегущую волну, имеет вид:

(1.10)

где

- комплексная амплитуда:

(1.11)

Формула (1.11) описывает комплексную амплитуду волны, распространяющейся в положительном направлении оси z в среде без потерь.

Комплексной амплитудой называется часть математического описания гармонического процесса, не зависящая от времени

Формула (1.5) является действительной частью формулы (1.10).

Обратите внимание на следующий факт. Модуль комплексной амплитуды не зависит от расстояния. Это характерно для любой плоской волны, распространяющейся в среде без потерь.

Для описания затухания электромагнитной волны вводится коэффициент затухания.

Коэффициент затухания характеризует уменьшение амплитуды электромагнитной волны при распространении в среде с потерями

В рамках метода комплексных амплитуд из коэффициента фазы и коэффициента затухания складывается комплексное волновое число:

(1.12)

где	β	- коэффициент фазы, действительная часть комплексного волнового числа, рад/м;
	α	- коэффициент затухания, мнимая часть комплексного волнового числа, , 1/м.

Комплексное волновое число вводится для описания изменения фазы и затухание волны при распространении в среде с потерями

Подставим эту формулу вместо коэффициента фазы в выражение (1.10). Получим:

(1.13)

Рассмотрим комплексную амплитуду этой волны:

(1.14)

По сравнению с формулой (1.11) описание комплексной амплитуды изменилось. Появилась зависимость амплитуды волны от пройденного расстояния, которую описывает exp(-αz). Пройденное расстояние в формуле (1.14) z – величина положительная. Обычно и коэффициент затухания больше нуля. Следовательно, амплитуда волны стала убывающей, а волна – затухающей.

Рис. 1.5. Мгновенные снимки затухающей волны

Мгновенные снимки затухающей волны приведены на рис. 1.5. Моменты времени, для которых изображены волны, сдвинуты на τ. За это время волна приходит некоторое расстояние, на котором затухает. Поэтому ее амплитуда убывает по мере возрастания координаты z.

Определяя длину волны, мы записали две формулировки: расстояние, через которое значения периодической функции повторяются и расстояние, проходимое волной за период. Очевидно, что первое определение подходит только для волны в среде без потерь. В среде с потерями с постоянным пространственным периодом будет повторяться только нулевое значение функции. Значит, длину затухающей волны необходимо определять по нулям, как это показано на рис. 1.5.

Все сказанное выше относится к плоской однородной скалярной волне. Плоская она по форме фронта, то есть поверхности постоянной фазы. Волна однородная, так как на поверхности фронта амплитуда ее постоянна. Скалярной эта волна является потому, что процесс описывался скалярной величиной u.

Очевидно, что волна может быть и не плоской и не однородной и не скалярной. Волна будет векторной, если волновой характер имеют компоненты некоторого вектора. Электромагнитные волны всегда описываются векторами.

Рассмотрим гармоническую волну, описываемую следующим соотношением:

(1.15)

И амплитуда u₀(x,y,z) и фаза φ(x,y,z) этой волны зависят от всех трех координат. Значит, формула, описывающая поверхность постоянной фазы, то есть волновой фронт, примет следующий вид:

(1.16)

В общем случае фронт этой волны не является плоскостью, то есть волна стала неплоской. Если на поверхности фронта амплитудаu₀(х, у, z)не постоянна, то волна становится инеоднородной.

Неоднородной называется волна, амплитуда которой не постоянна на поверхности волнового фронта

Очевидно, что распространение неплоских и неоднородных волн описывать значительно сложнее, чем плоских однородных. Однако неплоская и неоднородная волна может быть локально плоской и локально однородной в некоторой достаточно малой области пространства.

Локально плоской называется волна, часть фронта которой можно с достаточной точностью аппроксимировать плоскостью

Локально однородной называется волна, на части фронта которой амплитуду можно с достаточной точностью считать постоянной

Это позволяет использовать более простое описание плоской однородной волны для анализа распространения неоднородных волн со сложной формой фронта. Однако аппроксимация фронта волны плоскостью возможна и удобна далеко не всегда. Поэтому в необходимых случаях прибегают к описанию фронта волны цилиндром или сферой. Аппроксимации более сложными поверхностями, как правило, не применяются.

В цилиндрической или сферической системе координат уравнение поверхности фронта (1.16) примет простой вид:

	(1.17)

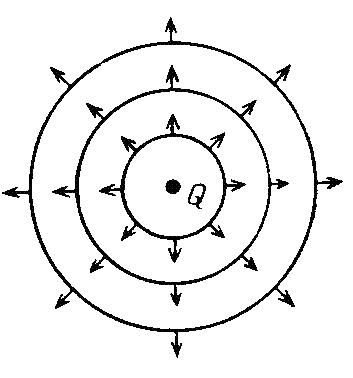
Рис. 1.6. Волна, распространяющаяся от источника

Если r - координата цилиндрической системы, то мы имеем цилиндрическую волну, если сферической – то сферическую волну.

Цилиндрической называется волна, фронт которой имеет форму кругового цилиндра

Сферической называется волна, фронт которой имеет форму сферы

На рис. 1.6 изображены сечения фронтов цилиндрической и сферической волн плоскостью рисунка, проходящей через источник. И у сферической и у цилиндрической волны эти сечения имеют форму окружности.

Стрелки на рис. показывают направление распространения волны. Эти волны распространяются от источника, поэтому называют расходящимися.

Расходящимися называются волны, распространяющиеся от источника

Теоретически может существовать и сходящаяся волна, поверхности фронтов которой сходятся к точке.

Сходящимися называются волны, поверхности фронта которой сходятся к точке

У сходящихся волн стрелки, показывающие направление распространения, будут направлены не наружу, как на рис. 1.6, а внутрь.

Кроме этого, волны имеют еще одну особенность. Для ее выяснения рассмотрим две механические волны – звуковую и волну на поверхности воды от брошенного камня.

Движение частиц при распространении звуковых волн иллюстрирует рис. 1.7, а. При распространении звуковой волны в среде перемещаются области повышенного и пониженного давления. На рис. величина давления отображается с помощью плотности точек: чем больше точек приходится на единицу расстояния, тем выше давление. Особенностью звуковых волн является то, что частицы среды колеблются вдоль направления распространения. Такие волны называются продольными. Применительно к электромагнитному полю определение продольной волны можно сформулировать следующим образом.

а

б

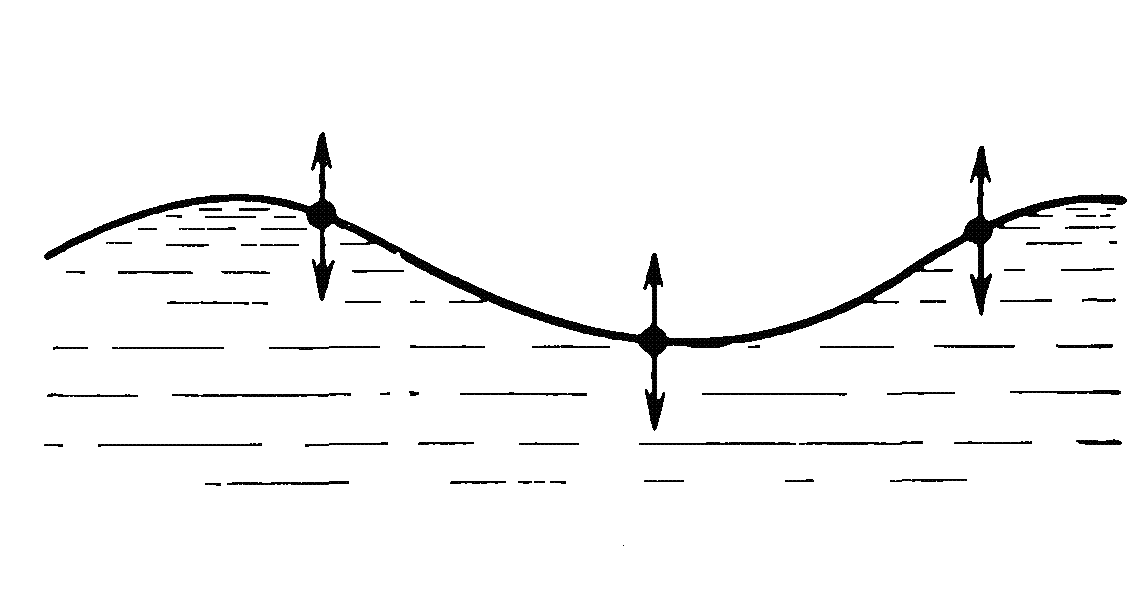
Рис.1.7. Смещение частиц в продольных (а) и поперечных (б) механических волнах

Продольной называется электромагнитная волна, в которой хотя бы один из векторов поля имеет продольную составляющую

Волны на поверхности воды от брошенного камня (рис.1.7, б) ведут себя иначе. Они расходятся от центра, то есть распространяются в горизонтальной плоскости. При этом частицы воды колеблются в вертикальной плоскости, перпендикулярно направлению распространения. Такие волны называется поперечными. Применительно к электромагнитному полю поперечные волны можно определить следующим образом.

Поперечной называется электромагнитная волна, векторы поля которой не имеют продольных составляющих