
C22013
.pdf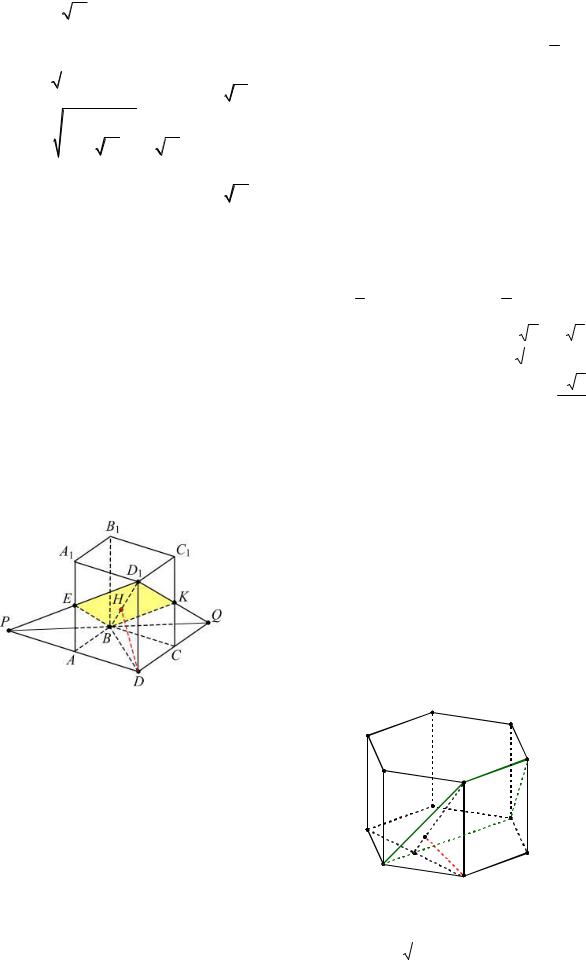
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
тогда MH 13 x. Выразим |
SH2 |
из |
||||||||||||||||||||
прямоугольных треугольников |
ASH |
и |
||||||||||||||||||||
SMH , |
и |
|
решим |
|
|
|
уравнение |
|||||||||||||||
4 x2 9 ( |
|
|
|
x)2 . Получаем |
x |
|
|
4 |
|
. |
||||||||||||
13 |
||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||
|
13 |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Тогда SH |
|
|
|
|
4 |
|
2 |
6 |
|
|
|
|
|
|
|
|
|
|||||
|
|
4 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
13 |
13 |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
|
6 |
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
||
Пример 12. В правильной четырех- |
||||||||||||||||||||||
угольной призме |
ABCDA1B1C1D1 |
стороны |
||||||||||||||||||||
основания равны 1, боковые ребра 2. Точка Е – середина ребра AA1 . Найти расстоя-
ние от вершины D до плоскости BED1.
Решение. Построим перпендикуляр из точки D на плоскость BED1 . Пусть точка K
– след плоскости BED1 на ребре CC1 (см.
рис. 11). Так как ED1 || BK (прямые пере-
сечения плоскостью BED1 параллельных граней параллельны), то из равенства прямоугольных треугольников EA1D1 и
BKC следует, что A1E CK , а тогда
C1K KC .
Рис. 11
Так как прямые ED1 и AD лежат в одной плоскости и не параллельны, то P ED1 AD есть общая точка плоско-
сти основания и плоскости BED1. Аналогично их общей точкой является
Q D1K DC .
Точки P, B и Q лежат на прямой пересечения указанных плоскостей.
Из равенства прямоугольных тре-
угольников |
EA1D1 и PEA следует |
PA A1D1. |
Аналогично получаем, что |
04.12.2012 |
11 |
DC CQ. Следовательно, |
прямоуголь- |
ных треугольник PDQ |
равнобедрен- |
ный и PD DQ 2. Тогда PQ 2
 2.
2.
В этом треугольнике DB биссектриса, а значит и высота, то есть DB PQ.
Тогда и D1B PQ по теореме о трех пер-
пендикулярах и PQ BD1D.
Плоскость BD1D BED1 по признаку перпендикулярности плоскостей. Следовательно, длина перпендикуляра DH , проведенного из точки D на прямую пересечения этих плоскостей BD1 , есть искомое расстояние, равное высоте прямоугольного треугольника BD1D, в котором
BD 
 2 , D1D 2 и BD1
2 , D1D 2 и BD1 
 6 .
6 .
D; BED DH |
D1D BD |
|
2 |
2 |
|
2 |
3 |
. |
|
|
|
|
|
|
|||||
1 |
BD1 |
|
|
6 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|||
Ответ: 2 3 . 3
Пример 13. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , ребра которой равны 1, найти расстояние от точкиA до плоскости A1B1С .
Решение. Прямая FC перпендикулярна АЕ и AA1, поэтому перпендикулярна плоскости AA1E1 (см. рис. 12). Пусть
FC AE G . Плоскость AA1E1 перпен-
дикулярна плоскости A1B1С , содержащей прямую FC, и пересекает ее по прямой A1G . Длина высоты AH в треугольнике
AA1G является искомым расстоянием.
|
|
D1 |
C1 |
|
E1 |
|
|
|
|
|
|
|
|
|
F1 |
|
A1 |
|
B1 |
|
|
|
||
|
|
|
|
|
|
|
D |
|
C |
|
|
|
|
|
E |
|
H |
|
|
|
|
|
|
|
F |
G |
|
B |
|
|
A |
|
|
|
|
|
|
|
|
|
|
Рис. 12 |
|
|
Так как в прямоугольном треугольнике |
||||
ADE AE |
|
|
|
|
|
AD2 ED2 , |
то есть |
||
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
AE |
|
, то AG |
3 |
. Из прямоугольно- |
|
3 |
|||||
|
2
го треугольника AGA1 находим
GA1 
 3 1
3 1 
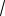 7 . 4 2
7 . 4 2
Высота AH равна
|
AG AA |
|
3 |
|
7 |
3 |
|
|
|
|
|
||
AH |
1 |
|
|
1 |
: |
|
|
|
. |
|
|
||
GA |
2 |
|
|
||||||||||
|
|
|
2 |
7 |
|
|
|
|
|
||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
3 |
. |
||||||
|
|
|
|
|
|
||||||||
|
Метод параллельных |
7 |
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||
|
прямых и плоскостей |
|
|
|
|
|
|
|
|||||
Данный метод опирается на следующие два утверждения. Расстояние от точки M до плоскости :
1) равно расстоянию до плоскости от произвольной точки P , лежащей на прямой l, которая проходит через точку
Mи параллельна плоскости ;
2)равно расстоянию до плоскости от произвольной точки P , лежащей на плоскости , которая проходит через
точку M и параллельна плоскости .
Пример 14. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки С1 до плоскости АВ1С .
Решение. Так как прямая А1С1 парал-
лельна AC , то прямая А1С1 параллельна плоскости АВ1С (см. рис. 13). Поэтому искомое расстояние h равно расстоянию от произвольной точки прямой А1С1 до плоскости АВ1С . Обозначим расстояние
от центра О1 |
квадрата |
A1B1C1D1 до плос- |
кости АВ1С через h. |
|
|
|
C1 |
|
B1 |
O1 |
D1 |
|
A1 |
|

 E
E







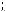 C
C
B
 O D
O D
A
Рис. 13
Пусть E – основание перпендикуляра, опущенного из точки О1 на прямую В1О, где O – центр квадрата ABCD. Покажем, что О1Е AB1C . Прямая О1Е лежит в плоскости BB1D1D, а прямая AC перпендикулярна этой плоскости (объясните). Поэтому О1Е АС и О1Е – перпен-
дикуляр к плоскости АВ1С , а О1Е h.
Так как В О |
|
|
|
|
2 |
, О О 1, то из пря- |
|||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||
|
1 |
1 |
|
2 |
1 |
|
|
|
|
|
|
|
|
||||||||||||
моугольного треугольника OВ1O1 |
найдем |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
||||||
ОВ |
|
1 |
1 |
3 |
|
Искомое |
расстояние |
||||||||||||||||||
|
|
|
|||||||||||||||||||||||
1 |
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
равно |
h |
BO OO |
|
|
|
2 |
1: |
3 |
|
|
|
3 |
|
. |
|||||||||||
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
2 |
2 |
|
|||||||||||||||
|
|
|
|
|
OB1 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||
Ответ: 3 . 3
Пример 15. В правильной шестиугольной пирамиде MABCDEF, стороны основания которой равны 1, а боковые рёбра равны 4, найти расстояние от середины ребра BC до плоскости грани EMD.
Решение. В правильном шестиуголь-
нике ABCDEF BD DE и BD 
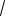 3.
3.
Точка O центр ABCDEF (см. рис. 14). Тогда MO высота пирамиды. Из прямоугольного треугольника MOD получа-
ем MO 
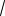 15. Апофему MN боковой
15. Апофему MN боковой
Рис. 14
грани DME находим из прямоугольного треугольника MDN
04.12.2012 |
12 |
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
MN |
MD |
2 |
DE |
2 |
|
3 |
7 |
|
|
||
|
|
|
|
|
|
|
. |
||||
|
|
|
|||||||||
|
|
|
2 |
|
|
2 |
|
|
|||
По признаку |
|
перпендикулярности |
|||||||||
плоскостей |
(DE MON , |
поскольку |
|||||||||
DE MO и |
DE MN ) |
|
MON DME . |
||||||||
Поэтому высота OH треугольника MON перпендикулярна плоскости DME . Из прямоугольного треугольника MON , в
котором OL |
BD |
|
3 |
, получаем |
|
|
|
||||||||||||||
|
|
2 |
|
|
|
|
|||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
MO ON |
|
|
|
|
|
|
|
: |
3 |
|
|
|
|
|
|
. |
||||
OH |
|
|
|
|
|
3 |
7 |
|
5 |
|
|||||||||||
15 |
|||||||||||||||||||||
|
|
|
|
|
|
|
7 |
||||||||||||||
|
MN |
|
|
|
|
2 2 |
|
|
|
|
|
||||||||||
Опустив из точки L перпендикуляры LQ на плоскость грани DME и LK на прямую DE, получим треугольник LQK , подобный треугольнику OHD . Так как расстояние от точки L до прямой DE
равно LK |
3 |
BD |
3 |
OL, то коэффици- |
|||||||||||||||||||
|
|
||||||||||||||||||||||
4 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
ент подобия |
этих |
треугольников |
равен |
||||||||||||||||||||
|
3 |
. Отсюда LQ |
3 |
OH |
3 |
|
|
5 |
|
|
|
|
45 |
|
. |
|
|||||||
2 |
|
|
7 |
28 |
|||||||||||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
Ответ: |
|
|
45 |
|
. |
|||||||||
|
|
|
|
|
|
|
|
|
28 |
||||||||||||||
|
|
|
Метод объёмов |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
При решении задач данного типа используется следующее утверждение.
Если объём пирамиды АВСМ равен VABCM , то расстояние от точки M до
плоскости , содержащей треугольник АВС, вычисляют по формуле
M, M, ABC 3VABCM .
SABC
В общем случае рассматривают равенство объёмов одной фигуры, выраженные двумя независимыми способами.
Пример |
16. |
Ребро |
куба |
ABCDA1B1C1D1 |
равно а. Найти расстоя- |
||
ние от точки C до плоскости BDC1 .
Решение. Искомое расстояние x равно высоте CQ (см. рис. 15), опущенной в
пирамиде BCDC1 |
из вершины C на ос- |
нование BDC1 . |
|
04.12.2012 |
13 |
Объём этой пирамиды равен |
|
|
|
|||||||||
1 |
S |
|
CC |
|
1 |
1 |
BC CD CC |
|
a3 |
|||
|
BCD |
|
|
|
|
|
|
|
. |
|||
3 |
|
|
|
|
||||||||
|
|
1 |
3 |
2 |
1 |
6 |
|
|||||
С другой стороны, так как треугольник
BDC1 равносторонний со стороной а
 2, объём пирамиды равен
2, объём пирамиды равен
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
SBC D CQ |
1 |
|
(a |
2)2 3 |
x |
a2 |
3 |
|
x. |
|||||||
3 |
3 |
|
4 |
|
|
6 |
|
|
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
B1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
C1 |
|
|
|
|
|
|
|
|
|
|
|
D1 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
B |
|
|
Q |
|
|
|
|
|
|
|
|
||
|
|
A |
|
|
R |
|
|
|
|
C |
|
|
|
|||||
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
Рис. 15 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
a3 |
a2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
3 |
|
x, из |
|||||||||
Получаем уравнение |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
6 6
которого находим x a 3 . 3
Ответ: a 3 . 3
Координатный метод
Расстояние от точки M x0 , y0 , z0 до плоскости , заданной уравнением ax by cz d 0, можно вычислить по формуле
M, |
|
ax0 by0 cz0 d |
. |
(3) |
||
|
|
|
|
|||
|
|
|
a2 b2 c2 |
|
||
Вывод уравнения плоскости. Приве-
дем один из способов получения уравнения плоскости, если известны координаты трех ее точек M(xM ; yM ; zM ),
N(xN ; yN ; zN ), P(xP; yP; zP ), не лежащих на одной прямой. Для этого нужно взять в общем виде уравнение плоскости ax by cz d 0, в котором a,b, c, d –
неизвестные числа. Подставив в него координаты точек M, N, P, получим систему уравнений:
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
axM byM czM d 0,axN byN czN d 0,
axP byP czP d 0.
Решив ее, найдем a pd,b qd, c rd
(если окажется, что |
d 0, то |
a pc, |
b qc; если d c 0, |
то a pb). Под- |
|
ставив в исходное уравнение и сократив на d 0, получим уравнение
px qy rz 1 0.
Иногда удобно использовать уравне-
ние плоскости в отрезках
x |
|
y |
|
z |
1, |
(4) |
|
|
|
||||
a b |
|
c |
|
|||
если известны координаты точек a;0;0 ,
0;b;0 , 0;0;c пересечения данной плоскости с координатными осями Ox , Oy , Oz соответственно.
Пример 17. Написать уравнение плоскости, проходящей через три точки
M 0;1;0 , N 1;0;0 , P 1;1;1 .
Решение. Записав в общем виде уравнение плоскости ax by cz d 0 и подставив в него координаты этих точек, получим:
a 0 b 1 c 0 d 0, (дляточкиМ)
a 1 b 0 c 0 d 0, (дляточки N)
a 1 b 1 c 1 d 0. (дляточки P)
Отсюда b d, a d и |
c d . Уравне- |
|
ние плоскости |
MNP |
имеет вид |
dx dy dz d 0 |
или |
x y z 1 0 |
после сокращения на d 0.
Пример 18. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все ребра которой равны 1, найти расстояние от точки A до плоскости DEF1 .
Решение. Введем систему координат, как показано на рисунке 16, и найдем координаты точек:
|
1 |
|
3 |
|
|
|
|
|
1 |
|
3 |
|
|
|
|
1 |
|
3 |
|
|
|
|
|
; |
;0 |
|
,D |
|
|
; |
;0 |
|
,E |
|
; |
;0 |
|
, |
|||||||
|
|
|
|
|
|
|||||||||||||||||
А |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
2 |
|
2 |
|
|
|
2 |
|
2 |
|
|
2 |
|
2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 1;0;1 . Пусть |
ax by cz d 0 – урав- |
нение плоскости DEF1 . Подставляя в него |
|
04.12.2012 |
14 |
координаты точек D, E , F1 , получим:
|
|
1 |
a |
|
|
3 |
|
|
b d 0, (дляточки D) |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
a |
|
|
3 |
|
|
b d 0, (дляточки E) |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
a c d 0. (дляточки F1) |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
B1 z |
|
C1 |
|
D1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
B |
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
O |
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 16 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b |
2 |
|
|
|
|
|
|
|
d , |
|||||||
|
Отсюда |
|
|
|
|
|
|
имеем |
|
a 0, |
|
|
3 |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|||||||||||||||||||||||||||||||||
c d . Уравнение плоскости DEF1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
при- |
|||||||||||||||||||||||||||||||||||||||||||
мет вид 2 |
|
|
|
|
y 3z 3 0. Вычислим рас- |
|||||||||||||||||||||||||||||||||||||||
|
|
|
3 |
|||||||||||||||||||||||||||||||||||||||||
стояние от точки |
А до плоскости |
|
DEF1 |
|||||||||||||||||||||||||||||||||||||||||
по формуле (3): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
|
2 |
|
|
|
|
3 |
|
3 0 3 |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
A; DEF1 |
|
|
|
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
02 (2 |
3)2 32 |
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
6 |
|
|
2 |
|
|
|
|
|
|
|
|
Ответ: |
2 |
|
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
21 |
|
|
. |
|
|
|
|
21 |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
21 |
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|||||||||||||||||
Пример 19. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки А1 до плоскости BDC1 .
Решение. Составим уравнение плос-
кости, |
проходящей через точки B(0;1;0), |
||||
D(1;0;0) |
и C1(1;1;1) |
(см. рис. 17). |
|||
Для этого подставим координаты этих |
|||||
точек |
в |
общее уравнение |
плоскости |
||
ax by cz d 0. |
Получим |
систему |
|||
уравнений |
|
|
|
||
b d 0, |
|
b d, |
|||
|
|
|
|
|
|
a d 0, |
|
или a d, |
|||
|
|
|
|
|
|
a b c d 0 |
c d. |
||||
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
z |
B1 |
|
|
A1 |
|
y |
C1 |
|
|
||
|
B |
D1 |
|
|
|
|
|
|
|
|
C |
A |
|
D |
|
|
|
x |
|
|
|
|
Рис. 17
Отсюда находим уравнение
dx dy dz d 0
или
x y z 1 0.
По формуле (3) находим расстояние от точки А1(0;0;1) до плоскости BDC1:
|
|
0 0 1 1 |
|
|
|
|
|
|
|
|
|
|
||
А; |
|
|
|
2 3 |
. |
|
|
|
|
|||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|||||||||
1 |
|
1 1 1 |
3 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
Ответ: |
2 |
3 |
|
. |
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
3 |
|
|
|
||||||
Векторный метод
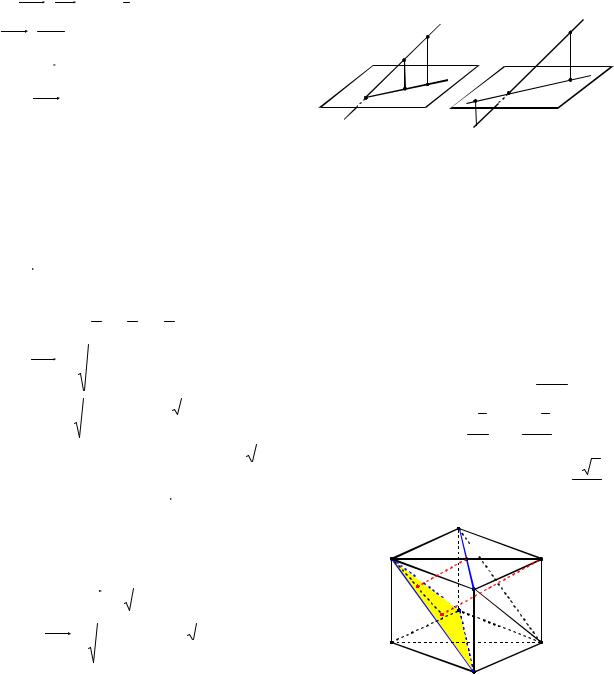
Пусть дана плоскость , содержащая два неколлинеарных вектора q1 и q2 , точка A принадлежит плоскости , точ-
ка M вне плоскости , MA m (см. рис. 18).
Неизвестные коэффициенты x, y находятся из условия перпендикулярности
вектора MP векторам q1 и q2 :
|
|
|
|
|
|
|
0, |
||
MP q 0, |
(m x q |
y q |
2 |
) q |
|
||||
|
1 |
|
|
1 |
|
1 |
|
||
|
|
|
|
|
|
0. |
|||
|
|
|
(m x q |
y q |
2 |
) q |
2 |
||
MP q2 0 |
|
1 |
|
|
|
||||
Искомое расстояние выражается следующим образом:
MP |
|
|
|
|
|
)2 . |
|
||||||
|
(m x q |
y q |
||||
|
|
|
|
1 |
2 |
|
Пример 20. В единичном кубе ABCDA1B1C1D1 найти расстояние от
точки А1 до плоскости BDC1 . |
|
||
Решение. |
Пусть |
AD a , |
AB b , |
AA1 c (см. |
рис. 19), |
тогда |
|a | |b | |
| c | 1, a b a c b c 0.
Выразим векторы DB, DC1, C1A1 че-
рез базисные a, b, c :
DB b a, DC1 b c , C1A1 a b .
Пусть МА1 BDC1 , где M BDC1.
Вектор C1M x DB y DC1 , поэтому
MA1 C1A1 C1M C1A1 (x DB y DC1).
Рис. 18
Чтобы найти расстояние от точки M до плоскости , то есть длину перпендикуляра MP (P ), представим вектор
MP в виде
MP |
|
|
|
MA AP m x q1 |
y q2 . |
||
04.12.2012 |
|
|
15 |
Рис. 19
Далее имеем |
|
|
|
|
|
|||
|
MA DB, |
MA DB 0, |
|
|||||
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
DC1 |
|
|
DC1 |
0 |
|
|
MA1 |
MA1 |
|
|||||
|
|
|
|
|
2 |
|
|
0, |
C A |
DB x DB y DC |
DB |
||||||
|
1 |
1 |
|
|
|
1 |
|
|
C1A1 DC1 x DB DC1 y DC12 0.
Так как
C1A1 DB ( a b)(b a) a2 b2 0,
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
DC1 DB (b c)(b a) b2 1, DC1 C1A1 (b c)( a b) b2 1,
2 |
|
|
|
|
|
|
|
|
|
|
|
DB (b a)2 b2 a2 2, |
|||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
DC (b c)2 |
b2 c2 2, |
||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
0 (x 2 y 1) 0, |
|
||||||||||
то имеем |
|
|
|
|
|
|
|
|
|
||
1 (x 1 y 2) 0 |
|
|
|||||||||
2x y 0, |
|
x 1/3, |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x 2y 1 |
|
y 2/3. |
|||||||||
Отсюда получаем |
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
2 |
|
|
|
||
MA1 a b |
|
(b |
a) |
|
|
|
|
(b |
c) |
||
|
|
|
|
|
|||||||
33
2a 2b 2c ,
|
|
|
|
|
3 |
|
|
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
2 |
|
|
2 |
|
2 |
|
2 |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
MA1 |
|
|
|
|
|
a |
|
|
b |
|
|
|
|
c |
|
|
|
|
|
|
|
|
|
|||||||
|
3 |
3 |
3 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
4 |
|
4 |
|
4 |
|
|
|
|
|
3 |
|
. |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
9 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
9 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
. |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: |
3 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Замечание. Вектор MA1 |
|
в данном ба- |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
|
|
|
|||||||
зисе имеет координаты |
|
|
|
|
; |
|
; |
|
|
, по- |
|||||||||||||||||||||
|
3 |
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
3 |
|
|
|
|
|
||||||||
этому длину этого вектора можно найти
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
по формуле |
MA |
|
|
a2 b2 |
c2 , то есть |
||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
2 |
|
|
. |
|||
MA |
4 |
|
4 |
|
4 |
|
3 |
||||||||
9 |
|
|
|
|
|
||||||||||
1 |
|
|
9 |
9 |
|
|
|
3 |
|
|
|
|
|||
Метод опорных задач
Применение данного метода состоит в использовании известных опорных задач, которые в большинстве случаев формулируются как теоремы.
Расстояние от точки M до плоскости можно вычислить по формуле
|
r |
, |
где M, , |
|
M |
, , |
|
||||||
1 r |
|
1 |
1 |
|
||
1 |
|
|
|
|
|
|
OM r, |
OM1 r1, MM1 O ; в част- |
|||||
ности, 1 , если r r1 (прямая m, проходящая через точку M , пересекает плоскость в точке O, а точка М1 лежит на прямой m (см. рис. 20а и 20б)).
04.12.2012 |
16 |
|
|
M |
|
M |
|
M1 |
|
|
|
m |
|
|
m |
|
O |
A1 |
A |
A1 O |
A |
 M1
M1
а б
Рис. 20
Пример 21. В единичном кубе ABCDA1B1C1D1 найти расстояние от точки D1 до плоскости АВ1С .
Решение. Используем найденное расстояние (пример 14) от точки С1 (от точ-
ки O1 ) до плоскости АВ1С . Опустим перпендикуляр D1F на прямую B1E (см. рис. 21). Тогда имеем
(D1, AB1C) (O1, AB1C) B1D1 , B1O1
(D1, AB1C) 
 3 2 2
3 2 2
 3 . 3 3
3 . 3 3
Ответ: 2 3 .
|
|
3 |
|
C1 |
|
||
B1 |
O1 |
D1 |
|
E |
A1 |
||
|
|||
F |
|
|
|
C |
|
|
|
B |
|
D |
|
|
|
||
A |
|
||
Рис. 21 |
|
||
Пример 22. Точки |
A, B, C, D являют- |
||
ся вершинами параллелограмма, ни одна из сторон которого не пересекает плоскость . Точки A, B, C удалены от плоскости на расстояние 2, 3, 6 соответственно. Найти расстояние от вершины D до плоскости .
Решение. Опустим перпендикуляры из вершин A, B, C и D на плоскость .
Точки A1, B1,C1, D1 – их ортогональные проекции на (см. рис. 22).
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Точка O – точка пересечения диагоналей параллелограмма ABCD, которая проектируется в точку O1 – точку пересечения диагоналей параллелограмма A1B1C1D1 (по свойству проекций). Так как точка O делит отрезки AC и BD пополам, то по свойству проекций отрезков точка O1 также делит отрезки A1C1 и
B1D1 пополам. Четырехугольники C1CAA1
и D1DBB1 – трапеции. Отрезок OO1 их средняя линия. Тогда
CC1 AA1 DD1 BB1 . 2 2
Отсюда DD1 CC1 AA1 BB1 и, так как
CC1 6, BB1 3, AA1 2, то DD1 5.
|
B |
C |
A |
O |
|
|
D |
|
B1 |
O1 |
C1 |
A1 |
|
D1 |
как МЕ – средняя линия в треугольнике SOA, DE – средняя линия в треугольнике
ОАL, то
|
3 |
|
1 |
|
92 |
|
|
3 |
|
1 |
|
92 |
|
M |
|
; 1; |
|
|
|
, |
K |
|
;1; |
|
|
|
. |
|
|
|
|
|
|
||||||||
|
3 |
|
2 |
|
3 |
|
|
3 |
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
Составим уравнение плоскости, проходящей через три точки С, М и K. Подставим координаты точек С, М и K в общее уравнение плоскости ax by cz d 0, получим систему уравнений
4
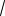 3 a d 0,
3 a d 0,
3
|
|
3 |
|
|
|
23 |
|
|
|
|
|
a b |
|
|
c d 0, |
||||
|
|
|
|
|
|
|
|||
3 |
|
3 |
|||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
3 |
|
a b |
23 |
|
c d 0. |
||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|||||
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
Рис. 22
Ответ: 5.
Решение одной задачи разными методами
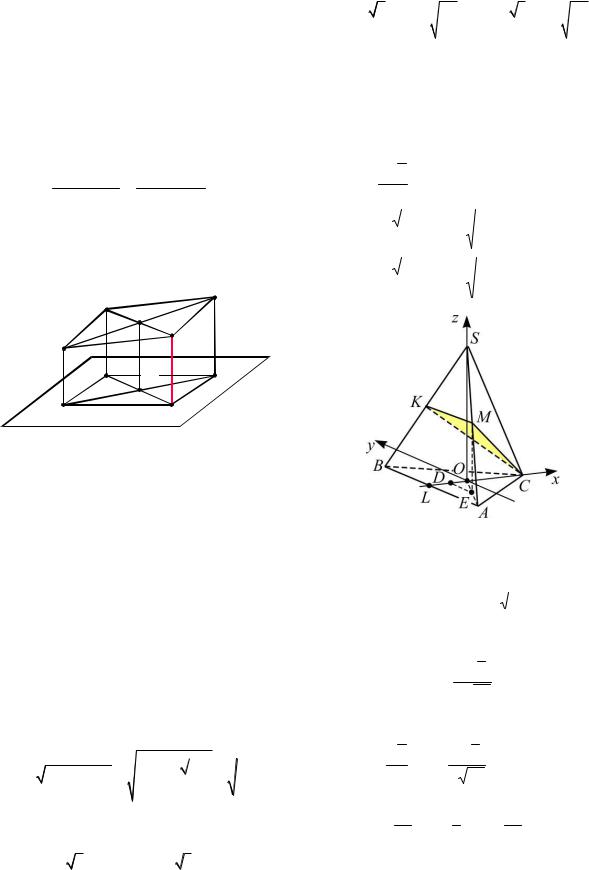
Пример 23. В правильной треугольной пирамиде SABC точка S – вершина. Точка M – середина ребра SA, точка K – середина ребра SB. Найти расстояние от вершины A до плоскости CMK, если
SC = 6, AB = 4.
Решение. 1-й способ (координатный метод). Пусть SO – высота пирамиды, которую найдем из треугольника SOC
(см. рис. 23):
|
|
|
|
|
|
|
4 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
92 |
. |
|||||
SO |
SC |
2 |
OC |
2 |
|
2 |
|
|
|
||||||||
|
|
|
6 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Введем систему координат, как показано на рисунке 23, и найдем координаты
4 |
3 |
|
|
2 3 |
|
|
точек C |
|
|
;0;0 , |
A |
|
; 2;0 . Так |
|
|
|
||||
|
3 |
|
|
3 |
|
|
|
|
|
|
|||
04.12.2012 |
|
|
|
|
|
17 |
Рис. 23
Вычитая из третьего уравнения второе,
определяем b 0 . Теперь из |
первого |
||||
уравнения выразим a |
|
3 |
|
d |
и подста- |
4 |
|
||||
|
|
|
|
||
вим во второе. Получим
c 5
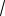 3 d . 4
3 d . 4
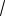 23
23
Уравнение плоскости СМK имеет вид

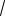 3 dx 5
3 dx 5
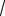 3 dz d 0
3 dz d 0
4 |
4 |
23 |
или

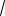 69x 5
69x 5
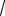 3 z 4
3 z 4
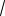 23 0.
23 0.
Воспользуемся формулой (3) расстояния от точки до плоскости
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
(A;CMK)
|
|
|
|
|
2 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
69 |
|
|
|
|
|
|
|
0 ( 2) 5 3 0 4 23 |
|
||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
69)2 02 (5 3)2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
23 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||
Ответ: 
 23 .
23 .
2
2-й способ (метод объемов). Так как середина отрезка SA точка M принадлежит плоскости СМK, то точки A и S равноудалены от этой плоскости (см. рис. 24). Расстояние от точки S до плоскости СМK высоте пирамиды SKMC, опущенной на основание KMC.
Найдем объём пирамиды SKMC и площадь треугольника KMC.
SM SK
VSKMC SA SB VSABC
|
1 |
|
1 |
V |
|
|
1 |
|
1 |
|
|
SO S |
|
|
|
|
||||||||
|
|
|
|
|
3 |
|
|
|
||||||||||||||||
2 2 |
|
|
SABC |
4 |
|
|
|
|
ABC |
|
||||||||||||||
|
|
|
1 |
|
|
92 |
|
|
16 |
3 |
|
|
2 |
23 |
|
. |
|
|||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|||||||||||||
12 |
|
|
4 |
3 |
|
|
|
|
||||||||||||||||
где SО – высота пирамиды SABC, опущенной на основание ABC (см. рис. 23).
S
K P
M
H
B C
L |
A
Рис. 24
Треугольник KMC равнобедренный KC = MC и KM = 2 (как средняя линия треугольника SAB). Найдем MC из треугольника ASC (как его медиану):
MC 1 
 2 AC2 2 SC2 AS2
2 AC2 2 SC2 AS2
2
1 
 2 42 2 42 42
2 42 2 42 42 
 17 . 2
17 . 2
04.12.2012 |
18 |
Тогда высота треугольника KMС, опущенная на KM из точки C, равна
MC |
2 |
|
KM 2 |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
17 1 4 |
||
|
|
||||||
|
|
|
2 |
|
|
|
|
1
и площадь SKMC 2 2 4 4.
Соответственно, искомое расстояние
(A;KMC) (S;KMC)
. |
3 VSKMC |
|
3 |
2 23 |
|
|
|
|
|
|
23 |
|
|||||
|
3 |
|
||||||
|
|
|
|
. |
||||
SKMC |
|
|
|
|||||
|
|
4 |
|
2 |
|
|||
3-й способ (поэтапно-вычислитель-
ный). Так как прямая BA параллельна плоскости СМK (BA|| KM) (см. рис. 24), то искомое расстояние равно расстоянию от любой точки этой прямой до данной плоскости.
Пусть точка L – середина стороны BA. Тогда SL BA и CL BA (как медианы равнобедренных треугольников, опущенные на основание) и BA SLC , а, следо-
вательно, и KM SLC . |
По признаку |
перпендикулярности |
плоскостей |
KMC SLC . |
|
Так как PC KMC SLC , то перпендикуляр LH, опущенный из точки L на PC , будет являться перпендикуляром к плоскости СМK и его длина будет равна искомому расстоянию.
Рассмотрим треугольник LSC. Так как точка P лежит на KM, то LP PS и площадь этого треугольника равна половине площади треугольника LSC.
1
SLSC 2 SO LC 2 23 ,
23 ,
где SO SC |
2 |
|
AC 2 |
|
2 |
23 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
высота |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
3 |
|
3 |
|
|
|
|||
пирамиды, а LC AC sin60 2
 3. Тогда
3. Тогда
SLPC |
|
1 |
SLSC |
|
|
. |
|
23 |
|||||||
|
|||||||
|
2 |
|
|
|
|
||
Найдем PC из треугольника LSC (как его медиану)
www.alexlarin.net
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
PC 1 
 2 LC2 2 SC2 SL2
2 LC2 2 SC2 SL2
2
1 
 24 72 32 4. 2
24 72 32 4. 2
Тогда LH 2SLPC 
 23 .
23 .
PC 2
Тренировочные упражнения
23. В единичном кубе ABCDA1B1C1D1 найдите расстояние от точки А до плоскости BDA1 .
24. Ребро куба ABCDA1B1C1D1 равно

 3. Найдите расстояние от вершины C до плоскости BDС1.
3. Найдите расстояние от вершины C до плоскости BDС1.
25. В кубе ABCDA1B1C1D1 , ребро которого равно 4, точки E и F – середины ребер AB и B1C1 соответственно, а точка P расположена на ребре CD так, что CP 3PD. Найдите расстояние от точки A1 до плоскости треугольника EPF .
26. В правильной четырехугольной призме ABCDA1B1C1D1 сторона основания равна 1, а боковое ребро равно 2. Точка M – середина ребра AA1 . Найдите расстояние от точки M до плоскости
DA1C1 .
27. (ЕГЭ, 2012). В правильной четырехугольной призме ABCDA1B1C1D1 стороны основания равны 1, боковые ребра равны 2. Точка E – середина ребра AA1 . Найдите расстояние от вершины 
 до плоскости BED1.
до плоскости BED1.
28. (ЕГЭ, 2011). В правильной треугольной призме ABCA1BC1 1 точка M – середина ребра AA1, точка K – середина ребра BB1. Найдите расстояние от вер-
шины А1 до плоскости СМK, если
AA1 6, AB = 4.
29. (ЕГЭ, 2012). В правильной треугольной призме ABCA1BC1 1 стороны основания равны 2, а боковые ребра равны 3. Точка D – середина ребра CC1 . Найдите расстояние от вершины C до плоскости AB1D.
30. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, найдите расстояние от точки А до плоскости BFE1 .
31. Дан правильный тетраэдр ABCD с
ребром 
 6. Найдите расстояние от вершины A до плоскости BDC .
6. Найдите расстояние от вершины A до плоскости BDC .
32.В правильной треугольной пирамиде SABC точка S – вершина. Точка M – середина ребра SA, точка K – середина ребра SB. Найдите расстояние от вершины A до плоскости CMK, если SC = 6,
AB = 4.
33.Известно, что в треугольной пирамиде все плоские углы при вершине – прямые. Найдите длину ее высоты, если длины ее боковых ребер равны a, b и c.
34.Ребро AD пирамиды DABC перпендикулярно плоскости основания АВС. Найдите расстояние от вершины A до плоскости, проходящей через середины
ребер AB , АС и AD, если AD 2
 5,
5,
AB AC 10, BC 4
 5.
5.
35.В правильной четырехугольной пирамиде PABCD сторона основания равна 3, высота 2. Найдите расстояние от вершины A до грани PCD.
36.В правильной четырехугольной пирамиде SABCD (с вершиной S) сторона основания равна 2 и высота равна 1. Найдите расстояние от точки D до плоскости
BCS.
37.На продолжении ребра SK за точку K правильной четырехугольной пирами-
ды SKLMN с вершиной S взята точка A так, что расстояние от точки A до плоскости MNS равно 24. Найдите длину от-
резка KA, если SL 2
 41, MN 16. 38. В правильной шестиугольной пи-
41, MN 16. 38. В правильной шестиугольной пи-
рамиде SABCDEF с основанием ABCDEF сторона основания равна 5, а боковое ребро равно 8. Точка K – середина ребра SB. Найдите расстояние от точки A до плоскости KDF.
04.12.2012 |
19 |
www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
1.4. Расстояние между скрещивающимися прямыми
Расстояние между двумя скрещиваю-
щимися прямыми равно длине отрезка их общего перпендикуляра.
Для нахождения расстояния между скрещивающимися прямыми можно воспользоваться одним из четырех приведенных ниже способов.
1.(Метод построения общего пер-
пендикуляра или поэтапно-вычисли-
тельный метод). В этом случае строится общий перпендикуляр двух скрещивающихся прямых (отрезок с концами на этих прямых и перпендикулярный каждой из них) и находится его длина.
2.(Метод параллельных прямой и плоскости). В этом случае строится плоскость, содержащую одну из прямых
ипараллельную второй. Тогда искомое расстояние будет равно расстояние от ка- кой-нибудь точки второй прямой до построенной плоскости.
3.(Метод параллельных плоско-
стей). В этом случае данные скрещивающиеся прямые заключаются в параллельные плоскости, проходящие через них, и находится расстояние между этими плоскостями.
|
C |
l1 |
l2 |
|
|
|
C1 |
A |
H |
|
Рис. 25
4. (Метод ортогонального проекти-
рования). В этом случае строится плоскость, перпендикулярная одной из данных прямых, и строится на этой плоскости ортогональная проекция другой прямой (см.
рис. 25).
(l1;l2) (A; BC1) AH,
где A l1 , l1, BC1 ортогональ-
ная проекция l2 |
на плоскость , |
H ос- |
04.12.2012 |
|
20 |
нование перпендикуляра, опущенного из
Aна BC1.
Продемонстрируем применение всех
указанных методов на следующем простом примере.
Пример 24. В кубе, длина ребра которого равна a, найти расстояние между ребром и диагональю, не пересекающей его грани.
Решение. В качестве примера найдем расстояние между ребром AA1 и диаго-
налью D1C (см. рис. 26). Прямые AA1 и D1C скрещивающиеся. Используя каждый из отмеченных способов, покажем, что расстояние между ними равно a .
1-й способ (см. рис. 26а). Так как
A1D1 AA1 и A1D1 D1C , то A1D1 общий перпендикуляр двух скрещивающихся прямых AA1 и D1C. Расстояние между
AA1 и D1C равно A1D1 a .
2-й способ (см. рис. 26б). Так как плоскость DD1C1, содержащая D1C, па-
раллельна AA1, то расстояние от AA1 до DD1C1 равно a .
3-й способ (см. рис. 26в). Плоскость DD1C1, содержащая D1C, параллельна плоскости AA1B1 , содержащей AA1, и расстояние между ними равно a.
|
B1 |
C1 |
|
B1 |
C1 |
|
A1 |
D1 |
d |
A1 |
D1 |
d |
|
a |
B |
a |
B |
|||
C A |
C |
|||||
A |
D |
A |
D |
|||
|
|
аб
|
B1 |
C1 |
|
B1 |
C1 |
|
A1 |
D1 |
d |
A1 |
|
D1 |
|
a |
B |
a |
B |
d |
||
C A |
C |
|||||
A |
D |
A |
|
|||
|
D |
вг
Рис. 26
4-й способ (см. рис. 26г). Плоскость ABC перпендикулярна прямой AA1. Точ-
www.alexlarin.net
