C22013

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.

гда сторона основания данной пирамиды равна

AN

2d

.

sin60

3sin

В прямоугольном треугольнике ADO

AO

2

AN

2d

(так как O AN ),

3

3sin

DO AO tg

2d

.

3cos

Находим объём пирамиды

V1 DO SABC

3

1

2d

3

2d 2

3

3cos

4

3sin

2d3

.

9 3sin2 cos

Ответ:

2d3

.

9 3sin2

cos

Пример 91. Боковые рёбра наклонной треугольной призмы ABCA1B1C1 равны 6 см. Сечение плоскостью, пересекающей все боковые ребра призмы и перпендикулярной им, представляет собой треугольник, стороны которого относятся как 9:10:17. Найти площадь боковой поверхности этой призмы, если известно, что объём пирамиды A1ABC равен

288 см3.

где l длина бокового ребра, S и P – площадь и периметр перпендикулярного ему сечения соответственно, Sбок пло-

щадь боковой поверхности, получим

VABCA1B1C1 AA1 SKLM или 864 6SKLM .

Отсюда SKLM 144 см2.

Найдем периметр треугольника KLM . Пусть его стороны равны 9x,10x,17x.

Тогда PKLM 36x, а полупериметр p 18x . По формуле Герона, получим

SKLM p(p 9x)(p 10x)(p 17x) 36x2 .

Из	уравнения			36x2	144	получаем
x 2	см.		Следовательно,		PKLM	72 см.
Тогда S		бок	l P	6 72	432 см2.

Ответ: 432 см2.

Метод введения вспомогательного отрезка

Пример 92. Все боковые грани четырехугольной пирамиды – правильные треугольники. Расстояние от центра боковой грани до плоскости основания пирамиды равно b. Определить объём пирамиды.

E

A1 B1

K		17x	L
		C1
A	9x	10x	B

M

C

Рис. 103

Решение. Так как объём VA1ABC 288

см3, то VABCA1B1C1 3VA1ABC 864 см3. Пусть

треугольник KLM указанное в условии сечение, перпендикулярное ребрам призмы (см. рис. 103). Используя формулы

VABCA1B1C1 l S , Sбок l P ,

04.12.2012

71

F

A

K

D H OB

C

Рис. 104

Решение. Пусть сторона основания данной пирамиды ABCDE равна x, основание высоты пирамиды обозначим через О, основание апофемы к стороне AD –

через K (см. рис. 104). Тогда OK x , 2

высота EK в равностороннем треуголь-

нике равна x 3 . Из прямоугольного тре- 2

угольника EOK находим

www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.

OE 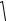x23 2 2x 2 x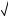22 .

Если F – центр боковой грани, Н – основание перпендикуляра, опущенного из точки F на основание пирамиды, то FH b. Из подобия треугольников EOK и FHK получаем

EO EK 3 и EO 3 FH .

FH FK 1

	Отсюда		x 2	3b,	x 3		b.	Значит,
						2
		2
	площадь	основания			пирамиды			равна

18b2 , высота пирамиды – 3b, объём данной пирамиды равен

V1 18b2 3b 18b3 . 3

Ответ: 18b3 .

Метод введения вспомогательного угла

Пример 93. В правильной четырехугольной пирамиде ABCDE (Е – вершина) через середины сторон АВ и AD проведено сечение, плоскость которого параллельна ребру ЕА. Найти объём пирамиды, если сторона основания равна a и площадь сечения S.

Решение. Плоскость сечения пересекает плоскости AED и АВЕ по прямым GH и FJ соответственно, параллельным АЕ. FG ||BD, так как FG – средняя линия в треугольнике ABD (см. рис. 105).

E

K

J SH

C

T

BQD

F R G

A

Рис. 105

В квадрате ABCD AС BD. Так как AQ – проекция АЕ на основание пирами-

04.12.2012

ды и

AQ FG , то FGHJ –

прямоуголь-

ник. Плоскости FGH и BDE пересека-

ются по прямой JH .

EQ HJ S ,

Пусть

AC FG R,

RS CE K ,

EAC .

Так

как

1

AQ

a

,

RQ

2

то

из

треугольника

2

4

RQ

a

.

RQS получаем RS

2

cos

4cos

Далее в треугольнике АЕС по теореме

Фалеса

EK

AR

1

, а в треугольнике

EQC

ED

AC

4

по

теореме

Фалеса

имеем

QT

EK

1

(Т – проекция точки K на

EC

QC

4

плоскость основания пирамиды), то есть

QT 1QC a 2 . Значит, 4 8

SK TQ a2 . cos 8cos

Площадь сечения равна

S SFGHJ SJKH

5a2

a 2

a 2

1

a 2

a 2

.

2

4cos

2

2

8cos

16cos

Отсюда cos

5a2

. Тогда

16S

sin

256S2 25a4

и

16S

tg

256S2 25a4

.

5a2

Высота пирамиды

EQ AQtg

a

tg

2

и объём пирамиды

2

1

a2

a

256S2

25a4

V

2

2

5a2

3

a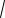512S2 50a4 . 30

Ответ: a512S2 50a4 . 30

72

www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.

Метод введения нескольких вспомогательных элементов

Пример 94. Найти объём прямоугольного параллелепипеда, диагональ которого равна 14, периметр основания – 20 и периметр меньшей боковой грани – 32.

Решение. Пусть в параллелепипеде

ABCDA1B1C1D1	D1B 14,	AB a,
BC b, B1B c с	условием	a b	(сде-
лайте рисунок самостоятельно).
Из условия задачи имеем
a2 b2 c2 196,	a2 b2	c2	196,
a b 10,	a 10 b,
b c 16.	c 16 b.

Получаем квадратное уравнение

3b2 52b 160 0,

имеющее корни 4 и 40 (не удовлетворя-

	3
ет условию	a b 10).	Тогда b 4,
a 6, c 12	и V 288.	Ответ: 288.

Метод опорных задач

● Объёмы пирамид с общей высотой пропорциональны площадям их оснований.

Пример 95. В правильной четырехугольной пирамиде SABCD точка F делит ребро ВС в отношении 1:3 (считая от точки С). Найти, в каком отношении делит объём пирамиды плоскость DSF ?

S

B

A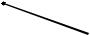FC

D

Рис. 106

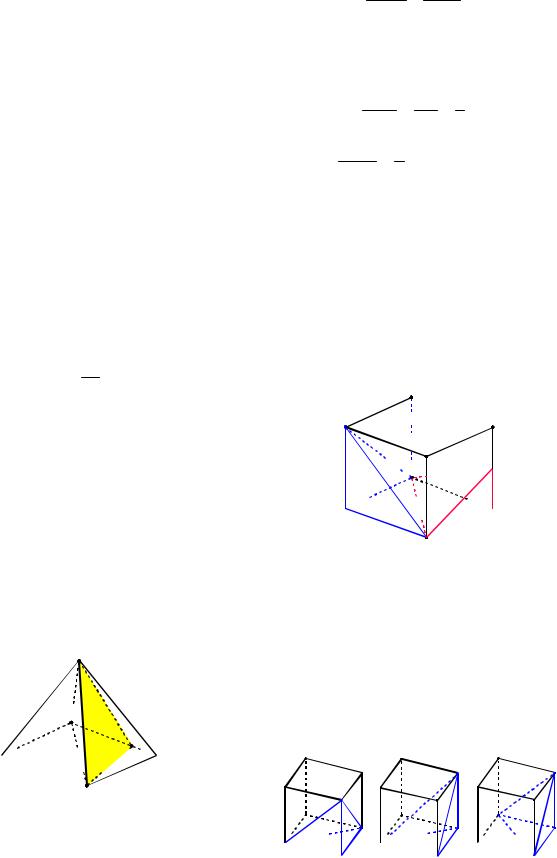
Решение. Так как данная пирамида и части, на которые она разбивается плоскостью сечения (см. рис. 106), имеют одинаковую высоту, то отношение объёмов частей равно отношению площадей оснований:

04.12.2012

73

VSABFD SABFD .

VSFCD SFCD

Площади треугольников ABD и BDC равны. Для треугольников с общей высотой имеем

SDCF CF 1 .

SDBF BF 3

Поэтому SABFD 7 .

SFCD 1

Ответ: 7:1.

● Объёмы пирамид с равновеликими основаниями пропорциональны проведенным к нему высотам.

Например, в кубе ABCDA1B1C1D1 (см.

рис. 107) объемы пирамид A1 ABD и MBDC относятся как 2:1, где М – середина ребра C1C .

B1

A1 C1

D1

BM

AC

D

Рис. 107

● Пирамиды с равновеликими основаниями и равными высотами – равновелики.

Например, в кубе ABCDA1B1C1D1 (см.

рис. 108) пирамиды A1 ABD, D1ABDи D1ACD равновелики.

	C1	C1	C1
B1	D1B1	D1B1	D1
	A1	A1	C A1
C		C

B DB DB D A A A

Рис. 108

www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.

● Отношение объёмов подобных многогранников равно кубу коэффициента подобия.

Пример 96. Площадь основания пирамиды равна 3, объём пирамиды также равен 3. Проведены две плоскости, параллельные основанию пирамиды. Площади получившихся сечений равны 1 и 2. Найти объём части пирамиды, расположенной между плоскостями.

D

C2 B2

C1A2B1

A1 B

C

A

Рис. 109

Имеем

Решение. Обо-

значим сечения через A1B1C1 и A2 B2C2 (см. рис. 109), причем

SA1B1C1 S1 2,

SA2B2C2 S2 1,

SABC S 3,

объемы пирамид

VABCD V ,

VA1B1C1D V1 ,

VA2B2C2D V2 .

	V										3									3
							S								2								8
		1					1																			,
		V					S								3								27
V												3								3
							S	2								1								1
	2																									.
		V					S								3								27

Отсюда искомый объем равен

		8		1			8 1
V V
	3										.
1 2		27		27			3

Ответ: 8 1. 3

Отношение отрезков можно заменить отношением объёмов пирамид с общим основанием (см. рис. 110)

DH DF VDABC ,

OH OG VOABC

где DF и OG – высоты пирамид.

04.12.2012

74

D

B

CGHF

A

O

Рис. 110

Пример 97. На рёбрах АВ, BD и DC пирамиды ABCD взяты точки M, L и K

так, что AM	1		AB,	BL	1	BD,
3				4

DK 2 DC . В каком отношении плос-

5

кость KLM делит отрезок, соединяющий середины ребер AD и ВС?

Решение. Обозначим середины AD и ВС через P и Q соответственно (см. рис. 111). В сечении получится четырехугольник, но для решения задачи достаточно рассмотреть отношение объемов пирамид PMLK и QMLK с общим основанием

MLK .

Если SABD a, то

S

DPL

DP

DL

S

ABD

1

3

a

3a

,

8

DA DB

2 4

S

BML

BM

BL

S

ABD

2

1

a

a

,

BA BD

3 4

6

S

AMP

AP

AM

S

ABD

1

1

a

a

,

AD AB

2 3

6

				3					1			1											7a
S	PML	1													S		ABD								,
									6			6										24
				8
V				KD			V									2	V					2V				,
	KABD			CD					ABCD					5								5
V			SMPL		V										7				2V					7V			,
														24
PKLM			SABD					KABD										5				60

где VABCD V .

www.alexlarin.net

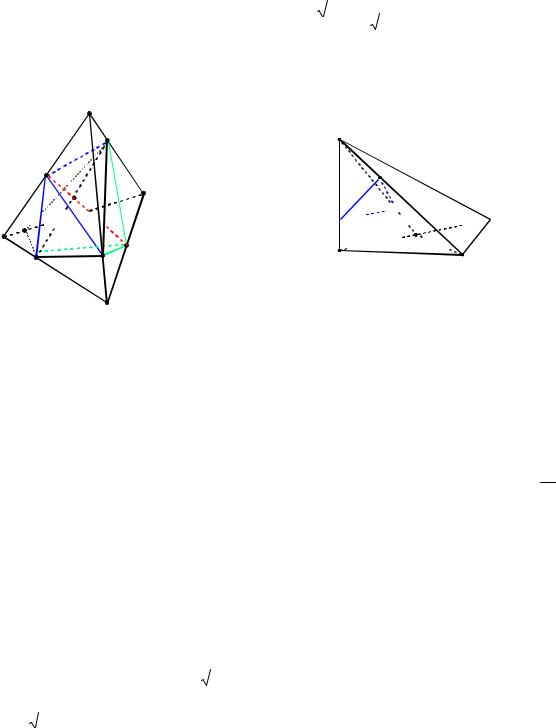
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.

	Аналогично получаем V										11V			(до-	V			1	AD S									1		AD AC BC sin C
						QKLM				60					3							ABC					6
	кажите самостоятельно!). Отношение															1	6				14		8						1		56.
																				3
		PN		VPKLM		7V	:	11V				7	.		6									3			2
																Так как медиана BT делит площадь
		QN VQKLM			60		60			11
															треугольника ABC пополам, то объём
					D										пирамиды DATB будет равен																	V	28.
																											2
							K													D
			P		N					C																N

J

A	Q
M	L

C M P

T

A B

Рис. 112

	B
	Рис. 111
	Ответ:		7	.
		11
● Пусть в пирамиде MABC на рёбрах
MA,	MB и MC или на их продолжениях
взяты соответственно точки		A1, B1,C1
так,	что MA1 :MA k , MB1	:MB m

MC1 :MC n. Тогда объёмы пирамид MA1B1C1 и MABC связаны формулой

VMA1B1C1 k m n VMABC . (*)

(См. опорную задачу 12 глава 3 п. 3.4).

Пример 98. В основании пирамиды DABC лежит треугольник ABC, в ко-

тором

C 30 ,

AC 14,

BC

8

,

3

точка T

– середина AC . Боковое ребро

AD равно 6

и перпендикулярно плос-

3

кости ABC.

На ребрах AD, BD и отрез-

ке

DT

взяты соответственно точки

M,

N,

P

так,

что AM : MD 2:5,

DN : NB 2:5 и

TP: PD 7:5. Найти

объём пирамиды DMNP.

Решение. Так как ребро AD перпендикулярно плоскости основания, то объем V пирамиды DABC равен

04.12.2012

75

Точки M, N, P лежат на ребрах пирамиды DATB (см. рис. 112), поэтому по формуле (*) получаем

V			DM					DP			DN			V
			DA
DMNP								DT			DB				DATB
	5			7			2		28			10		.
7			12			7					3

Ответ: 10 . 3

Пример 99. В правильной четырехугольной пирамиде MABCD все рёбра равны. Точки P и N – середины рёбер BM и DM . В каком отношении делит объём пирамиды сечение, проходящее через прямую AP параллельно диагонали основания BD?

Решение. Так как точки P и N – середины ребер BM и DM, то PN – средняя линия треугольника BMD и PN || BD. Так как через точку P можно провести единственную прямую, параллельную BD и секущая плоскость также параллельна BD, то PN лежит в плоскости сечения (см. рис. 113а).

Так как пирамида правильная, то MO – высота пирамиды (O – точка пе-

ресечения	диагоналей	основания),
MO BMD CMA.
Пусть точка E PN MO, тогда E –
середина	MO. Тогда прямая	AE также

www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.

		M
	K		N			M
P
	E				K
C				D		E
	O				Q
B					C	O	A
		A
						б
		а
		Рис. 113
лежит	в плоскости			сечения		и пусть
K AE CM ,			и		четырехугольник
APKN	– описанное			в	условие сечение
пирамиды.
На выносном чертеже (см. рис. 113б)
проведем отрезок OQ|| AK . Тогда,							ис-
пользуя теорему Фалеса, получаем KE –
средняя	линия		треугольника			OQM	и
QK KM ,		а OQ –		средняя линия тре-
угольника		CKA	и	CQ QK .		Следова-
тельно,	точка K		делит ребро			CM так,

что MK : MC 1:3.

Плоскость CMA разбивает каждую из пирамид MABCD и MAPKN на две равные треугольные пирамиды. Используя соотношение (*), получаем

V

MK

MP

MA

V

MC

MPKA

MB MA

MBCA

1

1

1 V

1

V .

2

3

MBCA

6

MBCA

1

Аналогично, VMKNA 6 VMCDA .

Соответственно, объём пирамиды MAPKN будет составлять шестую часть объема данной пирамиды, а секущая плоскость будет делить объём в отношении 1:5.

Ответ: 1:5.

● Пусть a и b – длины двух противоположных ребер тетраэдра, d – расстояние, а – угол между ними. Тогда объём тетраэдра можно вычислить по

формуле V 1 abdsin . 6

(См. опорную задачу 9 глава 3 п. 3.4).

Пример 100. Дан единичный куб АВСDA1B1C1D1 . Найти объём пирамиды АB1CD1.

Решение. Имеем АB1 CD1 2 (см.

рис. 114). Расстояние между скрещивающимися прямыми АB1 и CD1 , лежащими в параллельных плоскостях, равно 1. Угол между ними равен 90 , так как АB1 ||DC1 и CD1 DC1 . Следовательно,

1

VAB1CD1 6 AB1 CD1 AD sin (AB1;CD1)

1 2 2 1 1 1 . 6 3

	B1
A1	C1
	D1

B

AC

D

Рис. 114

Ответ: 1 . 3

Пример 101. На диагонали грани единичного куба взяты точки М и N, а на скрещивающейся с ней диагонали соседней грани взяты точки P и Q. Известно,

что MN

1

,

PQ

1

.

Найти объём

2

3

тетраэдра MNPQ.

Решение.

Пусть

дан

куб

АВСDA1B1C1D1 (см. рис. 115). Отрезки

MN и PQ лежат на прямых

AB1 и

A1C1

соответственно.

Так как

DC1 ||AB1 , то

(AB1, A1C1) A1C1D 60 .

Так

как

прямые

AB1

и

A1C1 лежат в параллель-

ных плоскостях AB1С и A1C1D , то

(AB; AC ) (ABC; AC D)

1

.

1

1

1

1

1

1

3

Получаем

04.12.2012

76

www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.

VMNPQ	1		1		1			1					3		1	.
	6				3		3						2	72
		2
					C1
B1							Q								D1
								P
N									A1
					C
B			M												D
						A
			Рис. 115

Ответ: 1 . 72

● Пусть p и q – площади двух граней тетраэдра, a – длина общего ребра, – величина двугранного угла между этими гранями. Тогда объем тетраэдра может быть вычислен по формуле

V 2pqsin .

3a

(См. опорную задачу 11).

Пример 102. Найти объём пирамиды

ABCD,	в которой AB 4,	BC 5,
AD 6 ,	BD 7, CA 8, а двугранный
угол с ребром AB равен 60 .

D

Тогда искомый объем пирамиды равен

V 2 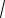172 92 3 5 7 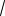3 :12 153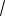35 . 16 2 64

Ответ: 153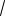35 . 64

Принцип разбиения и дополнения

Иногда при вычислении объема многогранника используют дополнение этого многогранника до пирамиды (призмы) или разбиение на эти фигуры.

Пример 103. В треугольной призме АВСA1B1C1 с объёмом 180 см3 проведено сечение через вершину A и середины рёбер BB1 и B1C1 . Найти объём отсеченной части призмы, содержащей ребро

CC1 .

Решение. Обозначим через М и N середины рёбер BB1 и B1C1 соответственно (см. рис. 117). Далее находим точки

S MN CC1 и P SA A1C1 , и в сече-

нии получим четырехугольник APNM .

	A1	B1
	S
		N
	P	C1
	A	L
		B
	C

7
6	5
B
4 60	C

8

A

Рис. 116

Решение. Используя формулу Герона, находим площади треугольников (см.

рис. 116) ABD и ABC:

SABD		17 9	3 5	и SABC	17 9 1 7	.
		4			4
04.12.2012

Рис. 117

Построим точку L MN BC . Пусть Н – высота призмы, Q – площадь основания. Объёмы пирамид SALC , SPNC1 и

MALB обозначим через V2 , V3 , V4 .

Точки М и N – середины ребер, поэтому

	BL	1	BC,	CL			3		BC. Значит,				S	ALC		3	Q .
	2				1		2				3				2
	Также SC					CC ,				SC		CC	и высота
			1	2			1			2		1

пирамиды SALC равна 3 H . 2

Объём

77

www.alexlarin.net

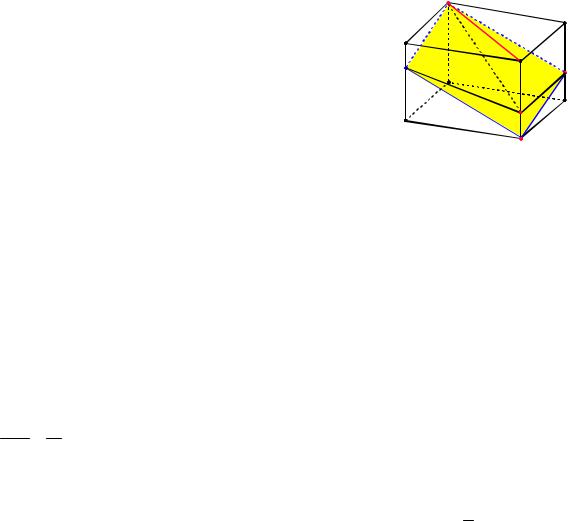
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.

V	1		3	H S	ALC		3	HQ	3	180 135.
2	3 2					4		4
Пирамида SPNC1								подобна пирамиде

SALC с коэффициентом k																					1		(SC :SC
																			3				1
1:3). Поэтому
								V k3V								135		5.
								3				2		27
	Так как М –									середина ребра BB1 , то
высота							пирамиды						MALB								равна			1	H.
															1								2
Кроме								того			BL						BC,						поэтому
				1										2
S	ALB						Q. Значит,
		2
V			1				1	H S	ALB				1	HQ						1			180 15.
												12							12
	4	3				2

Объём отсеченной части призмы, содержащей ребро CC1 равен

V2 V3 V4 135 5 15 115 (см3).

Ответ: 115 см3.

Пример 104. (ЕГЭ, 2008). Дан прямо-

угольный параллелепипед ABCDA1B1C1D1.

На его боковых рёбрах AA1 и BB1 лежат точки M и P соответственно так, что

AM :MA1 8:11, B1P: PB 2:1. Во сколько раз объём данного параллелепипеда больше объёма пирамиды с вершиной в точке P , основанием которой является сечение данного параллелепипеда плоскостью BMD1?

Решение. Объём V данного параллелепипеда равен V CB BA BB1 (см. рис. 118). Сечение параллелепипеда плоскостью BMD1 – параллелограмм BND1M , который делит его объём пополам и

C1N 8 (см. опорную задачу 21 в главе

NC 11 3 п. 3.4).

Так	как V			V		V				, то
	PBND M		2			NC D A MPB
		1				1	1	1	1
найдем	сначала	объём				многогранника
NC1D1A1MPB1. Для этого разобьем его на
04.12.2012										78

две пирамиды D1NC1B1P и D1PB1A1M и найдем объём каждой из них, учитывая, что противоположные ребра параллелепипеда равны.

						8				CC				2		BB
					19
S	NC B P										1	3					1		C B
												2							1 1
		1	1
								31			CB BB .
					57							1
							11			AA			2		BB
							19
S		PB AM									1	3					1		AB
												2							1 1
		1	1

71

AB BB .

114

1

V

D1NC1B1P

1

D C S

NC1B1P

1

31

V .

3

1 1

3 57

D1

A1

C1

N

D

B1

M

C

P

A

B

Рис. 118

V				1		D A S									1			71	V .
D1PB1A1M		3						1 1			PB1A1M		3				114
Тогда
V			V				1		31	V		1		71			V			V	.
PBND M		2					3	57			3		114				9
1

Ответ: 9.

Треугольную пирамиду можно достроить до параллелепипеда двумя способами.

1-й способ. Треугольник АВС достраиваем до параллелограмма АВЕС, затем до параллелепипеда ABECA1B1E1C1 (см. рис. 119). В этом случае

1

VABCA1 6VABECA1B1E1C1 .

(См. опорную задачу 7 глава 3 п.3.4).

www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.

E1

B1

C1

A1

E

B

C

A

Рис. 119

2-й способ. Проводим через каждое ребро тетраэдра плоскость, параллельную противоположному ребру (см. рис. 120). В этом случае рёбра исходного тетраэдра являются диагоналями граней получившегося параллелепипеда и

1

VABCD 3VDECFHAGB .

B

H

G

A

F

D

C

E

Рис. 120

Пример 105. В треугольной пирамиде боковые рёбра взаимно перпендикулярны

и имеют длины 70 , 99 и 126 . Найти объём пирамиды.

Решение. Данную пирамиду достраиваем до прямоугольного параллелепипеда. Тогда искомый объём равен

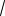V1 70 99 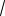126 21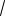55 . 6

Ответ: 21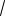55 .

Пример 106. Два противоположных ребра треугольной пирамиды равны а, два других равны b, два оставшихся – с. Найти объём пирамиды.

Решение. Достраиваем данный тетраэдр до параллелепипеда, проводя через каждое ребро плоскость, параллельную противоположному ребру. Согласно условию задачи получаем прямоугольный параллелепипед (диагонали в каждой грани равны). Пусть линейные размеры параллелепипеда соответственно равны AB x, AD y , AA1 z (сделайте рисунок самостоятельно). Исходя из условия, составим систему уравнений

x2 y2 a2,

y2 z2 b2,

2 2 2

z x a .

При сложении уравнений получаем

x2 y2 z2 1(a2 b2 c2). 2

Затем, вычитая из последнего равенства каждое равенство системы, находим

x2 1(a2 b2 c2), 2

y2 1(a2 b2 c2) , 2

										z2	1	( a2 b2 c2) .
	2
				Тогда искомый объём равен
											V		xyz
	3
			2
									(a2 b2 c2)(a2 b2 c2)( a2 b2 c2) .
	12
														Ответ:
				2
										(a2 b2 c2 )(a2 b2 c2)( a2 b2 c2)					.
	12

04.12.2012

79

www.alexlarin.net

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.

● Объём треугольного призматиче-

VDAFE

4 0 0

30 40.

ского тела

A1B1C1A2B2C2 , ограниченного

3

Ответ: 40.

треугольниками A1B1C1 и A2B2C2 , можно

вычислить по формуле

Пример 108. (ЕГЭ, 2007). Стороны

VA1B1C1A2B2C2

A1A2

B1B2 C1C2

SABC ,

АВ и АD основания прямоугольного па-

раллелепипеда ABCDABC D равны 7 и 5

3

соответственно,

1

1

1

1

AA1

где плоскость АВС перпендикулярна реб-

боковое

ребро

равно 3. Точки L, K, M лежат на ребрах

рам призматической поверхности (см.

AD, A1B1 , B1C1 так, что

AL: AD 3:5,

рис. 121).

В частности,

A1K : A1B1 4:7,

B1M : B1C1

2:5.

Най-

ти объём пирамиды с вершиной K и ос-

AA2

BB2 CC2

VABCA B C

SABC .

нованием AMC L.

1

3

2

2

2

Решение. Треугольник AKB1 является

A2

C2

ортогональной

проекцией

пирамиды

KAMC1L на плоскость

ABB1 (см.

рис.

123). Найдём необходимые величины:

	B2
A	C
	B
	C1

A1

B1

Рис. 121

(См. опорную задачу 13 глава 3 п.3.4).

Пример 107. Площадь основания АВС прямой треугольной призмы ABCA1B1C1 равна 30. Точки F, E, D лежат на рёбрах AA1 , BB1 , CC1 соответственно, причем AF 4. Найти объём треугольной пирамиды DAFE.

		Решение. Данную пирамиду DAFE
		B1	можно	представить
			как треугольное приз-
		E	матическое тело, ог-
	C1		раниченное		снизу и
		A1	сверху	треугольника-
			ми ADE и FDE соот-
	D		ветственно,		причем
		B	эти	треугольники
		F	имеют	две	общие
			вершины (см. рис.
	C	A	122).
			Находим искомый
		Рис. 122	объём

KB			3	7 3, MC				3	5 3,
								5
1		7			1
AL	3	5 3, SAKB				1		3 3		9	.
5		1			2			2

Пирамиду KAMC1L можно представить как призматическое тело, ограниченное треугольниками AKM и KLC1, причем эти треугольники имеют одну

B1	M	C1
K
A1	B
	D1	C

A

L D

Рис. 123

общую точку. Тогда искомый объём равен

V	AL MC1 0	SAKB		3 3	0		9	9.
3		1	3		2

Ответ: 9.

04.12.2012

80

www.alexlarin.net