IÒÅÎ Ð = I1 + I2 +

I3 =

m1L2

й

ж L

ц2

2

щ

m3R32 .

(2.5.12)

=

3

+ 4

к m1 з

+ R3 ч

+ m2l

ъ

+

2

к

и 2

ш

ъ

л

ы

Порядок виконання роботи

1. Розмістити важки m2 на однакових відстанях від осі обертання, внаслідок чого маятник повинен бути збалансованим.

2.Штангенциркулем виміряти радіуси двоступінчатого шківа r1 і r2.

3.Намотати нитку на шків з радіусом r1. Підвісити на гачок

нитки важок масою m.

4.Установити нижній край важка точно з фіксованою міткою на лінійці установки.

5.Одночасно відпустити важок і запустити секундомір.

6.Визначити час, за який важок опуститься до нижньої мі-

тки.

7.Визначити відстань h між мітками.

8.Експеримент провести по 3-5 разів для однакового поло-

ження важків m2m1 для радіуса шківа r1, при різних масах важків m на нитці, а потім повторити те ж для радіуса шківа r2. Результати всіх вимірів занести в таблицю 2.5.1.

9.Для обчислення теоретичного значення моменту інерції маятника Обербека необхідно виміряти довжину стержня

хрестовини L , його діаметр d , визначити масу кожного з чотирьох важків m2, які знаходяться на хрестовині, і їх довжину l0.

10. Виміряти діаметр стержня хрестовини d і відстань R0 від кожного важка до осі обертання. Дані вимірів записати в таблицю 2.5.2.

Обробка результатів експерименту та їх аналіз

1. За формулою (2.5.7) обчислити момент інерції маятника Обербека для різних радіусів двоступінчастого диска і маси важків m, знайти середнє його значення

52

2.Обчислити абсолютну і відносну похибки експерименту.

3.За формулою (2.5.12) обчислити теоретичний момент інерції маятника.

4.Порівняти результати, отримані з експерименту і

теоретичним шляхом, зробити відповідні висновки.

Контрольні питання

1.Основне рівняння динаміки для обертального руху твердого тіла. Момент інерції, момент сили, момент імпульсу. Обчислення моментів інерції тіл. Теорема Штейнера ( с.16-25).

2.Кінетична енергія обертового та поступального рухів твердого тіла (с.18-20).

3.Закони збереження імпульсу, моменту імпульсу й енергії

вмеханіці. Консервативні та дисипативні сили(с. 7-11, 23-26).

4.Вкажіть основні джерела похибок при експериментальному і теоретичному визначенні моменту інерції маятника Обербека. Спробуйте оцінити їх величину. Оцініть вплив кожного доданка розрахункової формули (2.5.12) на точність розрахунків.

Таблиця. 2.5.1

	m,	h,	Iтеор,		r1=			r2=
№ п/п
	кг	м	кг×м2	t, с	I1експ,	DI, кг×	t, с	I2експ,	DI, кг
					кг×м2	м2		кг×м2	×м2
1
2
3
С. зн.
								Таблиця 2.5.2
№		L	d	D	m1	l0	R0	m2	R3
1

53

2

3

С. зн.

54

Лабораторна робота 1.6 Визначення моментів інерції твердих тіл

за допомогою трифілярного підвісу

Мета роботи. Набуття навичок експериментального визначення моментів інерції твердих довільної форми та перевірка теореми Штейнера.

Прилади і матеріали. 1. Трифілярний підвіс. 2. Набір тіл (дисків). 3. Секундомір. 4. Штангенциркуль. 5. Рулетка. 6. Терези.

Теоретичні відомості

На практиці часто необхідні значення моментів інерції неоднорідних твердих тіл і тіл неправильної форми. У таких випадках моменти інерції визначають експериментальним шляхом. Одним із методів визначення моментів інерції є метод трифілярного підвісу. Трифілярний підвіс – кругла платформа, підвішена на трьох симетрично розташованих нитках, закріплених на її краях. Зверху нитки також симетрично прикріплені до диску трохи меншого діаметру, ніж діаметр платформи.

Платформа може виконувати крутильні коливання навколо вертикальної осі ОО′ (рис. 2.6.1), яка перпендикулярна до її площини і проходить через її центр мас. Центр мас платформи при цьому зміщується внаслідок закручування сталевих ниток вверх або вниз по осі обертання. Період коливань залежить від величини моменту інерції платформи. Цей принцип лежить в основі визначення моменту інерції методом трифілярного підвісу. Він дає можливість визначати моменти інерції тіл довільної форми. Це основна перевага методу трифілярного підвісу над іншими методами.

Нехай платформа масою m0 , обертаючись в одному напря-

мку, піднялася на висоту h . При цьому потенційна енергія платформи зросте на величину

Wп = m0 gh ,

(2.6.1)

де g − прискорення вільного падіння.

55

	B	r O′
	C1	α O1
h	A1
A	C	O	R
	Рис. 2.6.1

При обертанні платформи у зворотному напрямку потенціальна енергія перетворюється в кінетичну енергію обертового руху

	WK =	Iω 2	,	(2.6.2)
		2
	де I − момент інерції платформи відносно осі ОО′ , ω			− кутова
	швидкість платформи.

56

Платформа пройде положення рівноваги з максимальною кінетичною енергією. Нехтуючи силами тертя, виходячи із закону збереження механічної енергії, можна записати, що

m gh =	Iω	2
		max	,	(2.6.3)
0		2

де ω max − кутова швидкість платформи в момент досягнення нею

положення рівноваги.

Вважаючи, що платформа виконує гармонійні крутильні коливання, можна записати залежність кута зсуву платформи від часу

α = α 0	sinω t = α 0	sin	2π t	t ,	(2.6.4)
			T

де α ,α 0 − відповідно миттєве й амплітудне значення кута відхи-

лення платформи від положення рівноваги, t − поточне значення часу, T − період коливань.

Знайдемо кутову швидкість платформи, взявши похідну від

рівняння (2.6.4):

ω = dα

=

2π α 0 cos

2π

t .

(2.6.5)

T

dt

T

Очевидно, максимальне значення кутова швидкість прийме

при cos

2π

t = 1

. Отже

T

ω max =

2π α 0 .

(2.6.6)

T

h

Знайдемо

величину

зміщення

платформи

вгору при

повороті її на кут α 0 , вважаючи, що h1 +

h2

≈ 2l (рис. 2.6.1):

h = h1 − h2

=

h2

− h2

≈

h

2

−

h2

(2.6.7)

1

2

1

2 .

h1 + h2

2l

Із рис. 2.6.1 видно, що

h2

= l 2

−

(R −

r)2 ,

1

57

h2 = l 2

-

(AB)2

= l 2 - (R2

+

r 2 -

2Rr × cosα

0

) .

2

Підставивши значення h2

і h

2

в (2.6.7), маємо

1

2

2Rr(1 - cosα 0 )

4Rr sin

2 α 0

h =

=

2

.

(2.6.8)

2l

2l

При малих кутахα 0

значення синуса можна замінити його

аргументом sin

α 0

»

α 0

. Отже

2

2

h

=

Rrα

2

(2.6.9)

2l

0 .

Із рівнянь (2.6.6), (2.6.9) випливає, що момент інерції I0

ненавантаженої платформи відносно осі ОО′

I

0

= m0 gRr T 2 ,

(2.6.10)

4π

2l

0

де T0 − період коливань ненавантаженої платформи.

Момент інерції платформи, навантаженої тілом довільної

форми з масою m відносно осі ОО′ дорівнює
I =	(m0 +	m)gRr T 2	,	(2.6.11)
	4π	2l

де T − період коливань навантаженої платформи.

Момент інерції тіла, що знаходиться на платформі, відносно

осі ОО′ дорівнює
IТ = I − I0 .	(2.6.12)

Якщо на платформі знаходиться n однакових тіл і вони розміщені симетрично центру або в центрі платформи, то момент інерції кожного з них дорівнює

IТ =	I − I0	.	(2.6.13)
	n

58

Інтервал вимірювання моментів інерції тіл на цій лабораторній установці залежить від величини моменту інерції ненавантаженої платформи. Для того, щоб отримати досить ви-

соку точність вимірювання моменту інерції тіла IT різниця моментів інерції I − I0 повинна бути достатньо великою у порі-

внянні з значенням I0 , тому диск платформи виготовляють із легкого матеріалу.

В динаміці обертового руху важливу роль відіграє теорема Штейнера: Момент інерції тіла відносно довільної осі ZZ ′ дорівнює сумі моменту інерції цього тіло відносно паралельної осі ОО′ , що проходить через центр мас тіла, і добутку маси тіла на квадрат відстані між цими осями

I z = Ic + ma2 .

(2.6.14)

Теорему Штейнера легко перевірити за допомогою трифілярного підвісу. Для цього необхідно мати кілька однакових тіла правильної форми (диск, обруч). Спочатку визначають момент інерції одного або кількох тіл, розмістивши їх у центрі платформи так, щоб їх центр мас співпадав із віссю обертання платформи, а потім тіла розміщують симетрично на платформі і визначають їх момент інерції при такому розміщенні. Знайшовши момент інерції всіх тіл (формула 2.6.12) та поділивши його на кількість тіл, визначимо момент одного тіла, що знаходиться на відстані a від осі обертання. Визначивши відстань, масу і момент інерції тіла, покладеного в центр платформи, можна обчислити момент інерції цього тіла за теоремою Штейнера. Порівнявши отримані значення моментів інерції тіла, ми експериментально перевіримо теорему Штейнера.

59

Порядок виконання роботи та обробка результатів експерименту

1. Визначити геометричні розміри l, R, r установки та геометричні розміри RТ ,rТ досліджуваних тіл. Зважити платформу

та тіла. Результати вимірів занести в таблицю 2.6.1.

2. Привести платформу у коливальний рух. Для цього повернути нижню платформу на невеликий кут – 5-10° відносно положення рівноваги – і відпустити її. Секундоміром виміряти час 25-30 повних коливань і визначити період коливань (ненавантаженої платформи

T =	t	,	(2.6.15)
0	N

де N − число повних коливань платформи за час t .

Обчислити момент інерції I0 не завантаженої платформи

(формула 2.6.10). Результати записати в таблицю 2.6.1.

3. У центрі платформи розмістити досліджуване тіло. Визначити період коливання платформи з тілом Т1 . Результати

записати в таблицю 2.6.2. Обчислити момент інерції тіла за формулами (2.6.10), (2.6.11), (2.6.12).

4. У центрі платформи розмістити кілька тіл (бригада, порядковий номер якої парний, виконує роботу з двома тілами, а бригада, в якої порядковий номер непарний – з трьома). Визначи-

ти період коливання платформи з тілами в центрі T2 . Результати

записати в таблицю 2.6.2. Обчислити момент інерції тіла за формулами (2.6.10), (2.6.11), (2.6.12), (2.6.13).

5. На платформі симетрично центра розмістити тіла. Визначити відстань а від центра платформи до центра мас тіл та

період коливань платформи Т3 .Результати записати в таблицю 2.6.2. Обчислити момент інерції I3 тіла зміщеного відносно осі

60

ОО′ на відстань а за формулами (2.6.10), (2.6.11), (2.6.12), (2.6.13).

6.Обчислити теоретичне значення моменту інерції

ненавантаженої платформи I0T та тіл ITT (формули 1.48, 1.49,

1.50) відносно осі, що проходить через їх центр мас. Результат порівняти з експериментом.

7. За теоремою Штейнера (формула 2.6.14) обчислити теоретичне значення моменту інерції зміщеного диска. Порівняти експериментальне та теоретичне значення моменту інерції зміщеного диска відносно осі OO′ .

Контрольні питання

1.Момент інерції твердого тіла. Розрахунок моментів інерції простих тіл (диск, однорідний стержень, куля). Теорема Штейнера. Момент імпульсу. (с. 16-24).

2.Основне рівняння динаміки обертального руху (с.25-26).

3.Кінетична енергія тіла, яке бере участь в обертовому русі. Закон збереження енергії в механіці. Консервативні та дисипативні сили (с.1819, 9-12).

4.Переваги і недоліки методу трифілярного підвісу (с. 52-

58 ).

Таблиця 2.6.1. Дослідження характеристик установки.

Систематичні

R= м

l=

м

r= м

mo=

кг

похибки,

х

№

N

t. T, dT, R, dR, r, dr, mo,

dmo,

l

l,

I0,

eI,

м

п/п

с

с

с м

м м

м кг

кг

,

м

кг×м2

%

1

-

-

2

-

-

3

–

–

-

-

Ср.

зн.

61

Систематичні

D

R=

м

Dr=

Dmo

=

кг

похибки, Dх

м

№

N

t.

T,

dT,

R,

dR,

r,

dr,

mo, dmo,

I0,

εI,

п/п

с

с

с

м

м

м

кг

кг

кг×м2

%

1

-

-

2

-

-

3

–

–

-

-

Ср.

зн.

mo_– систематичні похибки, δT, δr, δmo– випадкові

R ,

r,

похибки.

Таблиця 1.2.2. Визначення моментів інерції тіл.

Одне тіло в центрі платформи

№ N1

t1, T1, dT1, m, Dm, dm,

I1,

DI1,

dI1,

eI,

п/п

с

с

с

кг

кг

кг

кг×м2

кг×м2

кг×м2

%

1

–

–

–

–

2

–

–

–

–

3

–

–

–

–

–

–

Ср.

зн.

Кілька тіл (два або три) в центрі платформи

№ N2

t2, T2, dT2, m, Dm, dm,

I2,

DI2,

dI2,

eI,

п/п

с

с

с

кг

кг

кг

кг×м2

кг×м2

кг×м2

%

1

–

–

–

–

2

–

–

–

–

3

–

–

–

–

–

–

Ср.

зн.

Кілька

тіл (два або три) на відстані а центра платформи

№ N3

t3, T3, dT3, m, Dm, dm,

I3,

DI3,

dI3,

eI,

п/п

с

с

с

кг

кг

кг

кг×м2

кг×м2

кг×м2

%

1

–

–

–

–

2

–

–

–

–

62

3		–	–	–	–
Ср.	–	–
зн.

63

Лабораторна робота 1.7 Визначення прискорення вільного падіння за допомогою

математичного та фізичного маятників

Мета роботи. Освоїти методи визначення прискорення вільного падіння за допомогою фізичного та математичного маятників.

Прилади і матеріали. 1. Оборотний фізичний маятник. 2. Математичний маятник. 3. Лінійка. 4. Секундомір.

Теоретичні відомості

Фізичним маятником називають тверде тіло, яке може здійснювати коливання навколо нерухомої точки Î , яка не збігається з його центром мас С (рис. 2.7.1). При відхиленні маятника від положення рівноваги на

кут β під дією складової

сили	земного	тяжіння
F =	mg sin β	виникає
обертальний		момент

M = F = mg sin β . Він намагається повернути маятник у положення рівноваги. Запишемо рівняння руху маятника, виходячи з основного рівняння динаміки обертального руху (вважаємо, що сили тертя відсутні):

O

β

C ′

F

FΙ Ι

Рис. 2.7.1 mg

	I	d 2β		= − mg sinβ ,	(2.7.1)
		dt	2

де I – момент інерції тіла відносно горизонтальної осі, що проходить через точку підвісу О. Знак мінус в лівій частині

64

(2.7.1) вказує на те, що момент сили M = mgl sinβ прагне повернути маятник у положення рівноваги, а кут відхилення відраховується у протилежному напрямі. У цій системі координат сила тяжіння відіграє роль квазіпружної сили. Оскільки на маятник не діють інші сили, крім квазіпружної, то його коливання можна вважати вільними або власними.

Поділимо рівняння (2.7.1) на

I

та візьмемо до уваги, що

для малих кутів відхилення β

≈ 0.01÷

0.015 рад. (b

» 5 ¸ 7o ) від

положення рівноваги sinβ

≈ β , одержимо:

d 2b

+

mg

b = 0

(2.7.2)

dt 2

I

Перевіримо розмірність множника, який знаходиться перед

β у рівнянні (2.7.2):

é

mg ù

кг

м

м

2

с− 2 = Гц2 ,

ê

ú =

с

=

I

кг × м

2

ë

û

і отримаємо, що розмірність цього виразу дорівнює розмірності квадрату частоти.

	Оскільки m > 0 , g > 0 , >				0	, I > 0 , то і		mg	> 0 .
								I
	Очевидно, що можна ввести таке позначення:
		w 02 =		mg					(2.7.3)
					I
	Із рівнянь (2.7.2, 2.7.3) маємо:
		d 2b			2
			+ w		0b	= 0 .			(2.7.4)
		dt 2

Ми одержали диференційне рівняння вільних коливань фізичного маятника. Його розв’язком буде гармонічна функція

β = β 0 cos( ω 0t + ϕ 0 ),

(2.7.5)

65

де β 0 – амплітудне значення кута відхилення, t – час, ϕ 0 – початкова фаза коливань.

У рівнянні (2.7.5) величина ω 0 повинна бути кратна 2π ,

тому що період функції cos x дорівнює 2π . Таким чином ω 0 – циклічна частота власних коливань фізичного маятника.

ω 0 =

2π ν

(2.7.6)

Із рівняння (2.7.3) випливає

ω

0

=

mg

.

(2.7.7)

I

Відповідно, власна частота та період коливань дорівнюють

1

ν =

mg

,

(2.7.8)

2π

I

T =

2π

I

.

(2.7.9)

mg

Математичним маятником називають матеріальну точку, підвішену на невагомій і нерозтяжній нитці, що коливається у

	вертикальній площині під дією			О
	сили тяжіння (рис. 2.7.2). До			ϕ
	математичного	маятника	за
	своїми фізичними власти-
	востями найбільше подібна си-			l	N
	стема, що складається з нероз-
	тяжної легкої нитки довжиною
	l , до одного кінця якої підві-			x F
	шена невеличка металева ку-
				Рис. 2.7.2	mg
	лька радіусом	R (l > > R ),	а

другий закріплений у нерухомому шарнірі. Можна вважати, що центр маси такої системи

66

збігається з центром мас кульки. Очевидно, що математичний маятник є частинним випадком фізичного.

Момент інерції маятника відносно точки підвісу O рівний

I =

ml2 .

(2.7.10)

Для математичного маятника при =

l із рівнянь (2.7.9) та

(2.7.10) маємо:

ml 2

T = 2π

I

= 2π

= 2π

l

.

(2.7.11)

mg

mgl

g

З рівняння (2.7.11) випливає, що період коливань математичного маятника не залежить від амплітуди коливань

(для малих відхилень) і маси маятника, а

визначається

лише

довжиною маятника

l та

прискоренням вільного падіння g .

Якщо визначити періоди коливань T1 ,

T2 для двох математичних маятників з різни-

l2

ми довжинами l1 та l2

(рис.2.7.3), то згідно з

рівнянням (2.7.11) маємо

l1

T

=

2π

l1

,

(2.7.12)

1

g

T

=

2π

l2 .

(2.7.13)

h h2

2

g

Із рівнянь (2.7.12, 2.7.13) випливає

g

=

4π 2 (l − l

)

=

4π 2

h

T

1

2

T 2 −

T 2

2

− T 2

h1

1

2

1

2

4π 2 ( l

−

l

)

g =

.

(2.7.14)

T 2

1

T 2

2

−

Рис.2.7.3

1

2

67

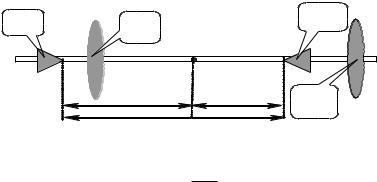
Для математичного (довжиною підвісу L ) та фізичного маятників, періоди коливань яких однакові, з рівнянь (2.7.9, 2.7.11) маємо

L =	I	.	(2.7.15)
	m

За теоремою Штейнера

I = IC + m 2 ,

(2.7.16)

де IC – момент інерції маятника відносно осі, що проходить

через його центр мас і паралельна до осі, яка проходить через точку підвісу.

Із рівнянь (2.7.15, 2.7.16) маємо

Р1	В			Р2
		C		O'
O
			′	А
	L
	Рис. 2.7.4
	L = +	IC .		(2.7.17)
		m

Величину L (рис.2.7.4) називають зведеною довжиною фізичного маятника. Легко показати, що зведена довжина фізичного маятника більша ніж відстань від центру мас маятника C до точки його підвісу O : L > .

Точку O′ (рис. 2.7.4), яка находиться на продовжені прямої OC на відстані L від точки підвісу, називають центром коливань фізичного маятника, або спрощено точкою коливань. Пере-

68

вернемо маятник на 180о, так, щоб точка його підвісу проходила через точку O′ , та знайдемо його зведену величину L′ :

Lў = lў+

IC

= L − l +

IC

=

mlў

m(L − l)

= l +

IC

+

IC

= l +

IC

= L

ml

ж

ц

ml

IC

mз l

+

− l ч

ml

и

ш

Отже зведена довжина маятника залишилася без змін, тому також не зміниться i період коливань маятника T ′ = T .

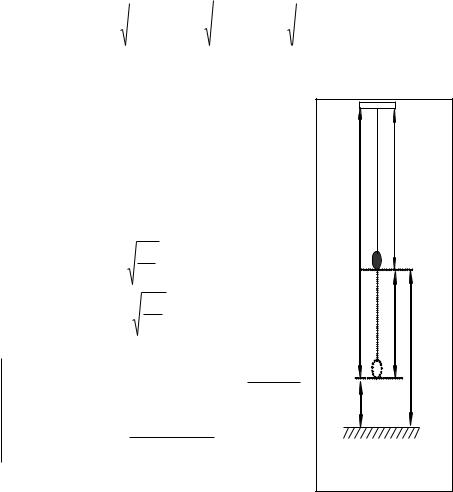
Точка підвісу O фізичного маятника і його центр коливань O′ є взаємними або спряженими. Ця властивість використовується в оборотних маятниках, які застосовуються для визначення прискорення вільного падіння.

Підставимо в рівняння (2.7.9) значення моменту інерції маятника згідно з рівнянням (2.7.11)

T = 2π		IC + m 2			(2.7.18)
			.
		mg

Якщо маятник оборотний, то

	T =	2π		IC +	m( ′ )2		.	(2.7.19)
				mg ′

Із рівнянь (2.7.19, 2.7.20) після нескладних перетворень маємо кінцеву формулу для розрахунку прискорення вільного падіння:

g =	4π 2	( + ′ )	=	4π 2 L	,	(2.7.20)
		T 2		T 2

де L – приведена довжина маятника, яка дорівнює відстані між точками підвісу оборотного маятника L = + ′ (рис.2.7.4).

Порядок виконання роботи та обробка результатів експерименту

Завдання 1

69

Визначення прискорення вільного падіння за допомогою математичного маятника.

1. Записати координату h1 положення нижньої частини ку-

льки маятника (рис. 2.7.3) в таблицю 2.7.1.

2. Відвести математичний маятник від положення рівноваги на кут 5-10о. Визначити час t1 повних n1= 20 -30 коливань маятника. Обчислити період коливань T1 . Результати занести у табли-

цю 2.7.1.

3. Підняти кульку маятника вгору (намотуючи нитку підвісу маятника на барабан) на 50-70 см або опустити її вниз. Визначити

положення h2 нижньої частини кульки. Визначити час t2 повних n2= 20-30 коливань маятника. Обчислити період коливань T2 . Результати занести в таблицю 2.7.1.

4.За формулою (2.7.14) визначити прискорення вільного

падіння.

5.Дослід повторити 5-7 разів. Визначити середнє значення прискорення вільного падіння та оцінити його похибку.

Завдання 2

Визначення прискорення вільного падіння методом оборотного маятника.

1. Поставити оборотній маятник опорною призмою Р1 на опору (рис. 2.7.3). Відвести маятник від положення рівноваги на

кут β ≈ 5 ÷ 7o та відпустити його. Визначити час t1 повних n1= 20-30 коливань маятника. Обчислити період коливань T1 відносно точки підвісу O .

2. Перевернути маятник на 180о. Визначити час t2 повних n2= 20-30 коливань маятника. Обчислити період коливань T2 відносно точки підвісу O′ .

70

3. Якщо різниця періодів коливань T1 − T2 > 0.05 c , то переміщуючи диск B маятника по його осі вгору або вниз, не змінюючи положення диска A та опорних призм P1, P2 , домо-

гтися її зменшення до 0,05 с.

4. Якщо періоди коливань співпадають з точністю до 0,01- 0,05 с, тобто T1 − T2 < 0.05 c , то провести 3-5 дослідів для визначення періодів коливань маятника відносно опорних призм P1, P2 , відстань L між опорними призмами. Результати дослідів

внести у таблицю 2.7.2. За формулою (2.7.20) обчислити прискорення вільного падіння та оцінити його похибку.

5. Порівняти результати завдань 1 i 2 та провести їх аналіз.

Контрольні питання

1.Гармонічні коливання. Вільні коливання. Основні характеристики вільних коливань. Диференційне рівняння вільних коливань. Пружинний, крутильний, фізичний та математичний маятники. (с.59-60).

2.Визначення прискорення вільного падіння за допомогою математичного та фізичного маятників. Залежність прискорення вільного падіння від широти місцевості та висоти над поверхнею Землі. (с.59-60).

3.Енергія коливальної системи.

Таблиця 2.7.1 №h1, м n1 t1, c T1, c h2, м n2 t2, c T2, c h, м g, м/с2 ε, %

			Таблиця 2.7.2
№ L, м	n1	t1, c T1, c n2	t2, c T2, c g, м/с2 ε, %

71

72