Потенціальна енергія визначається взаємним розміщенням тіл або частин тіла одна відносно одної.

На тіла, що знаходяться в потенціальних полях (гравітаційному, електростатичному) діють особливі сили, які називають консервативними. До консервативних сил також відносять пружні сили, що виникають при пружних деформаціях тіл. Це сили, робота яких залежить не від шляху, а лише від початкового і кінцевого положення тіла. Робота ж цих сил по замкнутому контуру дорівнює нулю. Крім консервативних сил, в природі існують неконсервативні або дисипативні (дисипація – розсіювання) сили, прикладом яких є сила тертя. Системи, в яких діють лише консервативні сили, називають консервативними, а системи, в яких діють лише дисипативні сили, – дисипативними. Усі живі організми належать до дисипативних систем.

Потенціальна енергія тіла масою m , піднятого над поверхнею Землі на висоту h , визначається рівнянням:

WÏ = mgh ,

(1.13)

де g − прискорення вільного падіння.

Знайдемо потенціальну енергію деформованої пружини. Елементарна робота, що виконується силою пружності при деформації (розтягуванні або стисканні) пружини на dx :

dA = Fdx = − kxdx , де k − коефіцієнт пружності.

Робота пружної сили при деформації пружини від 0 до x :

A = − тx kxdx =	−	kx2 .
0		2

Робота сили пружності буде від’ємною, оскільки напрям сили і зміщення протилежні. Робота зовнішньої сили, яка стискає

або розтягує пружину, буде додатною і дорівнюватиме kx22 . Ця робота йде на збільшення потенціальної енергії пружини.

11

Отже, потенціальна енергія деформованої пружини:

W	=	kx	2	(1.14)
ï		2

Робота консервативних сил дорівнює зменшенню потенціальної енергії системи:

A12 = WÏ 1 − WÏ 2 .

(1.15)

Закон збереження механічної енергії: повна механічна енергія замкнутої системи тіл, в якій діють тільки консервативні сили, залишається постійною.

Якщо ж у замкнутій системі, крім консервативних, діють також неконсервативні сили, наприклад, сили тертя, то повна механічна енергія системи не зберігається. Це пояснюється тим, що сили тертя здійснюють завжди від’ємну роботу – механічна енергія перетворюються у внутрішню. Отже, наявність сил тертя

взамкнутій системі приводить до зменшення її повної механічної енергії. Дія сил тертя спричинює перетворення механічної енергії

вінші, немеханічні види енергії. Але в цьому випадку виконується загальний закон збереження енергії: в ізольованій від будьяких зовнішніх впливів системі залишається постійною сума всіх видів енергії.

1.1.3.Абсолютно пружний і абсолютно непружний центральні удари тіл. Ударом тіл називають сукупність явищ, що виникають при короткочасній взаємодії тіл внаслідок зіткнення. Фізичні явища, які відбуваються під час удару, досить складні. Тіла при зіткненні деформуються, в них виникають сили пружності та тертя, також можуть виникати коливання і поширюватися механічні хвилі. При зіткненні тіл механічна енергія може перетворюватися в інші види енергії, наприклад, у теплову.

Систему тіл в момент зіткнення можна вважати замкненою, оскільки час взаємодії тіл досить малий і сили взаємодії досить великі у порівнянні із зовнішніми силами.

12

Спільну нормаль до поверхонь тіл у точці їхнього дотику при ударі називають лінією удару (рис. 1.1).

Удар називають центральним тоді, коли лінія удару

	n
C1 V		C2 V
1		2

m1 m2

Рис.1.1

проходить через центр мас тіл, а напрямок швидкостей тіл до зіткнення співпадає з лінією удару.

Процеси, що відбуваються при ударі залежать від фізичної природи тіл, їх розмірів та форми, швидкості руху тощо. Удари, які розглядають у фізиці, поділяють на абсолютно пружні, абсолютно непружні та реальні.

Абсолютно пружним називають такий удар, після якого тіла, що зазнали зіткнень, залишаються без залишкових деформацій, а кінетична енергія системи тіл до і після удару не змінюється. Абсолютно непружним називають такий удар, після якого деформації, викликані зіткненням тіл, повністю зберігаються, а тіла рухаються як єдине тіло. Подібний до абсолютно пружного удару ефект дає зіткнення кульок із слонової кості або високоякісної інструментальної сталі. Абсолютно непружний удар імітується зіткненням пластилінових кульок, влученням рушничних куль у підвішену мішень. До абсолютно непружних ударів наближаються процеси, що відбуваються при куванні і штампуванні. Найчастіше відбуваються реальні удари. За наслідками від зіткнень вони займають проміжне місце між абсолютно пружним та абсолютно непружним ударами.

Процес абсолютно пружного удару тіл уявно можна розділити на дві стадій:

13

І стадія – відбувається деформація тіл, їх кінетична енергія перетворюється потенціальну, швидкість зменшується до нуля, потенціальна енергія пружної деформації наприкінці стадії досягає максимуму.

ІІ стадія – потенційна енергія пружної деформації тіл перетворюється в кінетичну.

При абсолютно непружному ударі процес удару закінчується на першій його стадії. Частина кінетичної енергії відносного руху тіл перетворюється в немеханічні форми (тепло).

При абсолютно пружному ударі тіла цілком відновлюють свою форму, має місце закон збереження механічної енергії.

Отже при абсолютно пружному ударі діють закон збереження механічної енергії та закон збереження імпульсу, в той час як при непружному ударі – лише закон збереження імпульсу а закон збереження механічної енергії не діє, оскільки механічна енергія перетворюється в інші види (теплову та витрачається на роботу по деформації тіл тощо). Абсолютно непружний удар – типовий приклад, коли відбувається втрата механічної енергії під дією дисипативних сил.

Розглянемо абсолютно непружний центральний удар двох тіл (рис.1.2) на прикладі зіткнення двох пластилінових куль.

До удару		Після удару
V1	V2	U
m1	m2	m1 +m2
O		X

Рис.1.2

Нехай кулі рухаються вздовж прямої, що з’єднує їх центри, зі швидкостями V1 і V2 . У цьому випадку говорять, що удар є

центральним. Позначимо через U загальну швидкість куль після зіткнення.

14

Запишемо закон збереження імпульсу системи у векторній формі:

m1V1 + m2V2 = (m1 + m2 )U ,

(1.16)

де m1 і m2 – маси куль.

Знайдемо проекцію рівняння (1.16) на вісь ОХ

m1V1 + m2V2 = (m1 + m2 )U . Звідси одержимо швидкість куль після удару:

U = m1V1 + m2V2 m1 + m2

(рис. 1.2): (1.17)

(1.18)

Розглянемо центральний абсолютно пружний удар двох

куль (рис.1.3).
	До удару			Після удару
m1	V1	V2 m2	U1	m1 m2	U2
O					X

Рис.1.3

Нехай перша куля має масу m1 і швидкість до удару V1, а друга куля – масу m2 і швидкість V2. Визначимо швидкості куль U1 і U2 після удару, використовуючи закони збереження імпульсу

та енергії:

mV + m V = mU						+	m U		2
1	1	2	2	1	1		2
m V 2		m V 2		m U 2			m U 2
1 1	+	2 2	=	1 1		+		2 2 .
2
		2		2				2

Спроектуємо рівняння (1.19) на вісь ОХ (рис. 1.3):

m1V1 − m2V2 = − m1U1 + m2U2 . Перепишемо рівняння (1,20), (1.21) таким чином:

m1 (V1 + U1 ) = m2 (V2 + U2 )

m1 (V12 − U12 ) = m2 (U22 − V22 ) .

(1.19)

(1.20)

(1.21)

(1.22)

(1.23)

15

		Поділивши почленно рівняння (1.23) на рівняння (1.22), маємо:
				V1 − U1 = U2 − V2 , або					(1.24)
				U2 = V1 + V2 − U1					(1.25)
		Підставимо в рівняння (1.21) значення U2 та знайдемо U1 :
		U1 =	2m2V2 + (m2 −			m1 )V1 .			(1.26)
					m1 + m2
		Із рівнянь (1.25) і (1.26) маємо:
		U2 =	2m1V1 + (m1 −			m2 )V2 .			(1.27)
					m1 + m2
		Приклад: Знайти швидкості тіл після абсолютно пружного
удару (рис. 1.3), якщо їх маси m1 = 6кг ,							m2 =	2кг та швидкості
до удару V1 = 4м / с , V2 =				3м / с .
U1	=	2m2V2 + (m2 − m1 )V1		=	2 × 2 × 4 + (2 -		6)× 3	=	− 0.5м / с , (1.28)
		m1 + m2			6 + 2
U2	=	2m1V1 + (m1 − m2 )V2		=	2 × 6 × 4 + (6 -		2)× 3	= 7.5м / с . (1.29)
		m1 + m2			6 + 2
		Ми отримали від’ємне значення швидкості U 1 . Це означає,
що		її дійсний напрямок			буде протилежним				до показаного
на рис. 1.3.

16

1.2.Динаміка обертового руху

1.2.1.Момент сили. Момент імпульсу. Рівняння моментів. Важливі закони механіки зв’язані з поняттями моменту імпульсу або моменту кількості руху і моменту сили. Моментом сили відносно точки О (рис. 1.4) називається векторний добуток

радіуса-вектора r на вектор сил F :

	(1.30)
M = [r × F ].

Напрямок вектора моменту сили визначається за правилом векторного добутку. Він направлений вздовж осі обертання. Модуль моменту сили дорівнює:

M = rF sinα = rF	=	dF ,	(1.31)
де F = F sinα , d = r sinα .Величина	d	називається	плечем

сили – це найкоротша відстань між лінією дії сили і віссю обертання (рис.1.4).

	Плече сили	r	r		r
			F	=	F sinα
	d = r× sinα	r			Вісь обертання
		F

O

O

d

Лінія дії сили	O`

Рис. 1.4. Момент сили

Вектор моменту імпульсу визначається по аналогії з моментом сили: вектором моменту імпульсу L матеріальної точки називається векторний добуток її радіуса-вектора r , на вектор її імпульсу P :

	P]	(1.32)
L = [r ×

17

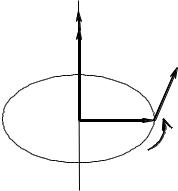
Він направлений вздовж осі обертання (рис.1.5):

O	′	ωr
		r
		L

r r

P = mV

r

m

ω

O

Рис. 1.5. Момент імпульсу матеріальної точки

Модуль моменту імпульсу дорівнює:
		L =	rP sinα			=	mrV sinα		,
де m − маса матеріальної точки.
Виявляється,	що величини					L і M		зв’язані між
оскільки
dL			P]		é		ù	é	dP ù
	=	d[r ´		=		dr
dt		dt			ê	dt	´ Pú +	ê r ´	ú .
					ë		û	ë	dt û

(1.33)

собою,

(1.34)

Оскільки

dr

=

mV , то

dr

dt

V

і P =

dt

P і перший доданок в

(1.34) дорівнює нулю. Отже матимемо:

dL

=

é

´

dP

ù

(1.35)

dt

ê r

dt

ú .

ë

û

Але, згідно

з

другим

законом

Ньютона,

dP

= F . Тоді

(1.35) прийме вигляд:

dt

dL

dt

=

[r

´ F ],

(1.36)

18

або

dL		(1.37)
	= M .
dt

Рівняння (1.37) називається рівнянням моментів: похідна за часом від моменту імпульсу матеріальної точки відносно нерухомої вісі дорівнює моменту діючої сили відносно тієї ж вісі. Зауважимо, що М являє собою сумарний момент зовнішніх сил.

1.2.2. Кінетична енергія тіла, яке перебуває в обертовому русі. Момент інерції. Визначимо кінетичну енергію твердого тіла, що обертається навколо нерухомої вісі ZZ ′ (рис. 1.6) з кутовою швидкістю ω .

Z′

ω

Vi	= ω × ri

ri

mi

ω

Z

Рис. 1.6. Кінетична енергія обертового руху твердого тіла

Виділимо на твердому тілі на відстані ri від осі обертання

точкову масу mi .Лінійна			швидкість виділеної						елементарної
маси становить:
		Vi = ω ri .							(1.38)
Кінетична енергія виділеної елементарної маси дорівнює:
T		m V		2		ω	2	m r 2 .
	=		i i		=				(1.39)
i			2				2	i i

19

Але кінетична енергія T всього тіла складається із кінетичних енергій його складових, тому

	n		m r 2ω	2			ω 2	n
T =	å		i i			=		å	mi ri2	.	(1.40)
			2				2
	i= 1							i= 1
Величину mr 2	позначимо через							IZ	і назвемо моментом
інерції матеріальної точки відносно вісі ZZ ′
			IZ =	mr 2 ,							(1.41)
де m – маса матеріальної точки, r							– відстань до осі обертання.
Момент інерції всього тіла відносно вісі ZZ ′										дорівнює сумі
моментів інерції його складових частин:
IZ	= ån		( IZ )i	=		ån		mi ri	2 .		(1.42)
	i= 1						i= 1

Отже, момент інерції твердого тіла чисельно дорівнює сумі добутків мас матеріальних точок (на які уявно розбивають тіло) на квадрати відстаней до їх осі обертання.

Момент інерції має певний фізичний зміст: є мірою інертності тіла при обертальному русі та характеризує масу тіла та її

розподіл	відносно осі обертання.			Аналогом			моменту інерції
у поступальному русі є маса тіла.
Кінетичну енергію тіла, що обертається відносно нерухомої
вісі ZZ ′	можна записати таким чином:
	T =	I	z	ω	2	.	(1.43)
				2

Індекс Z біля символу I у рівняннях (1.41,1.421.43) свідчить про те, що мова йде про момент інерції відносно вісі ZZ ′ , яка нерухома. Очевидно, що момент інерції цього ж тіла відносно іншої вісі зміниться, тому, говорячи про момент інерції, необхідно вказати вісь, відносно якої його обчислено.

У випадку однорідного тіла правильної форми операцію сумування заміняють на операцію інтегрування. Момент інерції будь-якого тіла можна обчислити через інтеграл:

20

I = ò r 2 dm ,	(1.44)
(m)

де інтегрування ведеться по всьому об’єму тіла, уявно розбитого на елементарні маси dm , кожна з яких характеризується своїм радіусом r відносно вісі обертання.

Знайдемо моменти інерції деяких тіл.

Момент інерції однорідного стержня відносно осі CCў, що проходить через його центр мас.

	C	dx
	x
	0	x
Х1=-l/2	C′	Х2=l/2
	Рис.1.7

Розглянемо однорідний стержень (рис. 1.7). Нехай його маса m , довжина l , лінійна густина γ (лінійна густина чисельно дорівнює масі, що припадає на одиницю довжини стержня

γ = ml ). Систему координат розмістимо таким чином, щоб

через її початок проходила вісь CC′ . Знайдемо момент інерції стержня відносно осі, що проходить через його центр мас. Ви-

ділимо на відстані

x від осі CC′ , яка проходить через центр мас

стержня, елементарну масу

dm . Елементарний момент інерції

виділеної маси відносно осі

CC′ складає: dIC

= x2 dm . Оскільки

dm = γ dx ,то dIC =

γ x2 dx , а момент інерції всього стержня

X 2

= l / 2

2

x3

l / 2

γ

й

ж l

ц3

ж − l ц3 щ

IC =

т

γ x

dx = γ

=

к

з

ч

− з

ч

ъ

=

3

3

X

1 = −

l / 2

−

l / 2

к

и 2

ш

и

2 ш

ъ

(1.45)

γ l 3

л

ы

ml2

=

=

12

12

21

При виведенні співвідношення (1.45) враховано, що γ l = m

.

Аналогічно знайдемо момент інерції однорідного стержня

відносно осі ZZ ′ , що проходить через один із його кінців. Систему координат розмістимо таким чином, щоб через її початок проходила вісь ZZ ′ .

X 2 = l

3

l

γ l

3

2

IZ =

ò γ x2 dx = γ x

=

= ml

.

(1.46)

X1 = 0

3

0

3

3

Момент інерції однорідного диска (циліндра) відносно вісі

CCў, що проходить перпендикулярно його площині через центр

C

(рис.1.8). Нехай маса

dх

диска т, радіус диска

R

,

х

С

густина

ρ . Виділимо

на

відстані х від центра (точ-

с

ка С) нескінченно тонкий

h

обруч

товщиною

dx ,

С’

елементарний момент іне-

R

рції

якого

дорівнює

Рис. 1.8. Момент інерції диска

dIC

= x2 dm .

Визначимо елементарну масу dm виділеного елементарного об'єму у вигляді тонкого кільця, беручи до уваги, що густина речовини ρ , а товщина диска h :

	dS = 2π xdx –	dm = ρ	dV = ρ hdS ,
де		площа	поверхні	виділеного
dIC	= 2π ρ hx3 dx . Проінтегруємо останній вираз:
		m	R
	IC =	тx2dm =	тx2 ρ 2π	xdx =
		0	0		mR2 ,
	= ρ h2π тR x3dx = ρ h2π			R4 =
		0		4	2

пояска, то

(1.48)

22

де m = ρ π R2 – маса диска.

Аналогічно можна знайти момент інерції диска з центральним отвором. Нехай радіус диска R , а радіус отвору r . Для цього рівняння (1.48) необхідно про інтегрувати від r до R

m

R

IC =

ò x2 dm =

ò x2 ρ 2π rdx =

0

r

m(R2 + r 2 ) ,

(1.49)

=

ρ

h2π

òR x3 dx = ρ h2π

R4 −

r 4

=

4

2

r

де m = 2π

(R2 −

r 2 )hρ

– маса диска.

Із (1.49) легко знайти момент

інерції диска без

отвору (

r = 0 ):

m(R2 +

IC =

r 2 )

=

mR2

,

(1.50)

2

2

та момент інерції обруча відносно осі, що проходить центр мас ( r ≈ R )

	IC = m(R2 + r 2 ) = m(R2	+ R2 ) = mR2 .		(1.51)
	2	2
Момент інерції кулі			2 mR2 .
		Ic =		(1.52)
			5
1.2.3.Теорема Штейнера. Ця теорема дозволяє знайти мо-
мент інерції тіла відносно довільної осі			ZZ ′ , якщо відомий мо-
мент інерції даного тіла відносно паралельної				осі CC′ , що
проходить через центр мас даного тіла (рис. 1.9), а саме:
Момент інерції тіла від-
носно довільної осі ZZ ′ дорі-		С		Z
внює сумі моменту інерції цьо-
го тіло	відносно паралельної
осі CCў,	що проходить через	m	a
центр мас тіла, і добутку маси
тіла на	квадрат відстані між
	23	C′		Z ′

Рис. 1.9. Теорема Штейнера

цими осями I z = Ic + ma2 – (1.53), де m − маса тіла, а − від-

стань між осями.

1.2.4. Основне рівняння динаміки обертового руху. Якщо на тіло (рис.1.10), яке може обертатися навколо довільної Z, діє

Z						момент сил M Z , а момент іне-
	M	z	= r	×	F	рції цього тіла відносно цієї ж
	ε z					осі IZ , то тіло набуде кутового
						прискорення:
					F	εrz = M z	.	(1.54)
IZ						Iz
			r			Рівняння	(1.54)		є
						основним рівнянням динаміки

ωобертового руху, в якому відіграє таку ж роль, як і другий

	закон	Ньютона	в	по-
Z′	ступальному русі.

Рис. 1.10

1.2.5. Момент імпульсу твердого тіла. Закон збереження моменту імпульсу. Для твердого тіла, яке обертається навколо осі ZZў з кутовою швидкістю ω , величина моменту імпульсу може бути визначена таким чином.

24

Уявно		Z′	ω
розіб'ємо тіло
на нескінчен-
			Li
но малі части-
нки – матері-			P =	mV
			i	i i
альні	точки
(рис.	1.11).
Розглянемо			ri
			mi
окрему таку i-
точку.		ω
Модуль	мо-
менту	імпу-	Z
льсу	даної	Рис. 1.11. Момент імпульсу твердого тіла

точки з масою
mi відносно вісі ZZў буде
L =	m rV sinα =	m	ω	r 2	,	(1.55)
i	i i i	i		i

де α = 90o , ω = Vr .

Для всього тіла матимемо (індекс z біля L означає, що мо-

мент імпульсу обчислено відносно осі ZZў):
	Lz =		е		miri	2ω z .	(1.56)
де ω z – кутова швидкість обертання тіла відносно вісі ZZў.
Згідно з (1.42) еn	miri	2	=		Iz , тому:
i= 1					Чωr
	L =		I	z			(1.57)
	z				z

Закон збереження моменту імпульсу: момент імпульсу замкнутої системи тіл залишається сталим незалежно від взаємодії її складових

r	n	r	n
L =	е	Li =	е Iiωri =	const ,	(1.58)
	i= 1		i= 1

25

де ω i – кутова швидкість i-го тіла, Ii – його момент інерції.

Закон збереження моменту імпульсу посідає важливе значення в механіці. У рівнянні (1.58) постійним залишається, як модуль моменту імпульсу так і його напрямок. На останній властивості ґрунтується робота гіроскопа. Гіроскоп це масивне тіло, яке може вільно обертатися з великою кутовою швидкістю навколо трьох осей. Основна його властивість: вісь гіроскопа зберігає свою орієнтацію в просторі незалежно від орієнтації основи гіроскопа. Гіроскопи широко застосовуються у навігації .

На основі закону збереження моменту імпульсу також пояснюється рух велосипедиста (мотоцикліста ). При русі велосипедиста (мотоцикліста ) вектор моменту імпульсу зберігає свою орієнтацію в просторі і велосипедист не падає.

26