Лабораторна робота 1.8 Вивчення затухаючих коливань пружинного маятника

Мета роботи. Освоїти методи визначення основних характеристик затухаючих механічних коливань.

Прилади і матеріали. 1. Пружинний маятник. 2. Лабораторна вага. 3. Важки. 4. Лінійка. 5. Секундомір.

Теоретичні відомості

Рухи тіл, які періодично повторюються в часі називають коливальними або коливаннями. Якщо коливання описуються законом синуса або косинуса, то їх називають гармонічними.

x = A0 cos(ω t + ϕ 0 )

(2.8.1)

де х – відстань коливальної точки від положення рівноваги, її називають зміщенням; А0 – максимальне зміщення коливальної точки від положення рівноваги або амплітуда коливань;ω t + ϕ 0 –

фаза коливань; (ϕ 0 – початкова фаза, ω – циклічна частота гармонічних коливань.

Розглянемо горизонтальний рух матеріальної точки масою т під дією пружини, один кінець якої жорстко закріплено

(рис.2.8.1).
Масою пружини і				k			m
тертям нехтуємо.		У
положенні	рівноваги							x
тіла	пружина
недеформована.		При			Рис.2.8.1.
зміщенні	тіла	від

положення рівноваги на величину х на нього діятиме лише сила пружності, яка, за законом Гука, дорівнює

F = − kx

(2.8.2)

де k – коефіцієнт пружності пружини, x – абсолютне видовження пружини. Тіло буде виконувати вільні коливальні рухи, тому коливальну систему “тіло – пружина” можна назвати пружинним маятником, а коливання – вільними.

73

Сила пружності направлена весь час проти прискорення тіла. Виведемо тіло з положення рівноваги та запишемо на основі другого закону Ньютона рівняння руху

m

d

2 x

= − kx , або

d 2 x

+

k

x = 0

(2.8.3)

dt 2

dt 2

m

Оскільки k > 0

i m > 0 , то

k / m >

0 ,

що дозволяє

ввести

нову змінну

k

ω 02

=

(2.8.4)

m

Із (2.8.3) i (2.8.4) маємо

d 2 x

+ ω 02 x =

0

(2.8.5)

dt 2

Фізичну систему, виведену із стану рівноваги i залишену без будь-якого зовнішнього втручання, в якій зміна одного із параметрів описується диференційним рівнянням (2.8.5) називають класичним гармонійним осцилятором, а коливальні рухи, які вона виконує – вільними коливаннями. Коливання є вільними або власними, якщо на тіло, що коливається, не діють інші сили, крім сили пружності. Щоб матеріальна точка здійснювала гармонічні коливання, не обов’язково на неї повинна діяти пружна сила. Досить, щоб при зміщенні тіла від положення рівноваги сила, яка діє на тіло, змінювалась за законом (2.8.2). Якщо сила за своєю природою не є пружною, але змінюється за законом (2.8.2), то її називають квазіпружною.

Диференційне рівняння (2.8.5) називають рівнянням вільних коливань. Його рішенням буде будь-яка функція часу,

яка перетворює це рівняння у тотожність.
Легко впевнитися,	що його розв’язком може	бути одна
з функцій:
x =	A0 cos(ω 0 t + ϕ 0 ) ,	(2.8.6)
x =	A0 sin(ω 0 t + ϕ 0 ) ,	(2.8.7)

де ω 0 – циклічна частота вільних коливань.

74

Підставивши функцію (2.8.6) і другу похідну від неї за часом у рівняння (2.8.5), переконуємося, що функція (2.8.6) є розв’язком диференціального рівняння (2.8.5).

Із рівняння (2.8.4) для пружинного маятника маємо
ω 0 =		k	.		(2.8.8)
		m

Відповідно частота та період вільних коливань дорівнюють

ν =

ω 0

=

1

k

,

(2.8.9)

2π

2π

m

1

.

T =

=

2π

m

(2.8.10)

ν

k

Розглянемо пружинний маятник, який виконує коливальні рухи у середовищі, яке чинить опір його руху, що дає підстави вважати – сила тертя не дорівнює нулю. Сила опору пропорційна

швидкості i завжди направлена проти руху маятника:
F = − r	dx	,	(2.8.11)
T	dt

де r – коефіцієнт опору.

Запас енергії коливальної системи буде витрачатися на виконання роботи проти сили тертя, тому амплітуда коливань буде зменшуватися з часом. Такі коливання є затухаючими.

Складемо рівняння руху для такого пружинного маятника.

m

d 2 x

+

r

dx

+

kx = 0

(2.8.12)

dt 2

dt

Поділимо рівняння (2.8.12) на масу маятника m .

d 2 x

+

r

dx

+

k

x = 0 .

(2.8.13)

dt 2

m dt

m

Введемо позначення:

r

=

2β ,

(2.8.14)

m

де β – коефіцієнт затухання.

75

Із рівнянь(2.8.4, 2.8.13,2.8.14) випливає:

d 2 x	+ 2β	dx	+ ω 02 x = 0 .	(2.8.15)
dt 2		dt

Рівняння типу (2.8.15) називають диференційним рівнянням затухаючих коливань. Легко переконатися, що його розв’язком можуть бути функції (рис. 2.8.2):

x =	A e− β t cos(ω	t +	ϕ	0	) ,		(2.8.16)
	0
x =	A e− β t sin(ω	t +	ϕ	0	) ,		(2.8.17)
	0
де x – зміщення точки від положення рівноваги,						A	– початкова
						0

амплітуда затухаючих коливань, ω – циклічна частота затухаючих коливань.

Амплітуда затухаючих коливань змінюється за законом

A = A e− β t .	(2.8.18)
0

	x = A e− β t Sin(ω t + ϕ	0	)
X	0

	A(t)	A = A0 e− β t
	A(t+

A(t+nT)

t

T	nT	Рис.2.8.2

Циклічна частота затухаючих коливань ω системи менша за власну циклічну частоту ω 0 :

ω = ω 02 − β 2 .			(2.8.19)

76

Швидкість затухання коливальних рухів характеризується декрементом затухання δ . Декрементом затухання називають відношення двох амплітуд, інтервал часу між якими дорівнює періоду коливаньT :

	A			A e− β t	= eβ T ,
δ =	t		=	0		(2.8.20)
	A			A e− β (t+ T )
		T )
	(t+			0

а натуральний логарифм відношення двох сусідніх амплітуд відповідно називають логарифмічним декрементом затухання:

λ = ln	An	= ln	At	= lnδ = β T .	(2.8.21)
	A( n+ 1)
			A(t+ T )

Визначивши експериментально логарифмічний коефіцієнт затухання λ і період коливань T , можна знайти коефіцієнт затухання коливальної системи

β

=

λ

.

(2.8.22)

T

Для зменшення похибки визначення β

вимірюють амплітуди,

різниця в часі між якими дорівнює не одному, а n періодів:

A

A

A e− β t

ln

0

= ln

t

=

ln

0

= nβ T = nλ ,

8.23)

A

A

A e− β (t+ nT )

n

t+ nT

0

звідки маємо:

ln

A0

(2.8.24)

A

,

λ

=

n

n

ln

A0

A .

(2.8.25)

β

=

n

nT

77

Порядок виконання роботи та обробка результатів експерименту

Завдання 1

Визначення коефіцієнта пружності

пружини.

1.

Підвісити

до

маятника

k

ненавантажену платформу (рис. 2.8.3).

Записати

значення

її

вертикальної

координати 0

у таблицю 2.8.1.

2. Помістити на платформу важок

m

масою m . Зафіксувати нову координату

платформи та визначити абсолютне ви-

довження пружини =

− 0 . Дослід по-

Рис. 2.8.3

вторити 3-5 разів із різними важками. Ре-

зультати занести у таблицю 2.8.1.

3. Обчислити для кожного досліду коефіцієнт пружності пру-

жини k =

mg

. Знайти середнє значення k

та оцінити похибку.

Завдання 2

Визначення основних характеристик вільних та затухаючих коливань пружинного маятника.

1.Зважити робоче тіло (важок) пружинного маятника на лабораторній вазі. Записати значення маси m0 важка у таблицю 2.8.2.

2.Зняти платформу маятника. Підвісити до пружини робоче тіло маятника без платформи. Зафіксувати та записати у

таблицю 2.8.3 величину 0 положення рівноваги маятника.

3. Відведіть маятник від положення рівноваги та відпустіть його. За допомогою секундоміра визначте час τ , протягом якого

маятник виконає		N = 15...30 повних коливань. Обчисліть період
T = τ / N	та	циклічну частоту затухаючих коливань
ω = 2π ν =	2π / T . Дані занесіть у таблицю 2.8.2.

78

4. Відведіть маятник до нижньої мітки шкали n . Визначте початкову амплітуду коливань маятника A0 = n − 0 . Відпустіть маятник та визначте амплітуди A1 , A2 , A3 ...Ak . Дані занесіть у таблицю 2. За формулою (2.8.24) визначте логарифмічний декремент затухання λ , а за формулою (2.8.25) коефіцієнт зату-

хання β	. Дані занесіть у таблицю 2.8.2.
5.	Визначте теоретичне	значення циклічної						частоти ω 0
	коливань маятника ω 0	=
вільних				k / m0		та порівняйте його з
значенням циклічної частоти ω		затухаючих коливань.
6.	Визначте початкову фазу коливань за величиною поча-
ткового зміщення маятника (при			t = 0, x		0	= − A	і	x0 = A0 Sinϕ 0
						0

тому ϕ 0 = arcsin(− 1) ).

7.Запишіть кінематичне рівняння затухаючих коливань для досліджуваного пружинного маятника. Для цього параметри A0 , β ,ω у рівнянні (2.8.17) потрібно замінити числовими значеннями.

8.Збільшіть опір маятника, підвісивши до навантаженої платформи один із наявних демпферів (легкий пінопластовий диск з великою площею поперечного перерізу) та проведіть досліди згідно з пунктами 1-7. Дані занесіть у таблицю 2.8.3 (її форма аналогічна до форми таблиці 2.8.2).

Контрольні питання

1.Гармонічні коливання. Вільні коливання. Основні характеристики вільних коливань. Диференційне рівняння вільних коливань. Пружинний, крутильний, фізичний та математичний маятники (с. 68-72 ).

2.Затухаючі коливання. Основні характеристики затухаючих коливань. Диференційне рівняння вільних коливань та його розв’язок (с. 70-72).

3.Енергія коливальної системи.

4.Закон Гука. Модуль Юнга ([1],с. 73-78).

79

Таблиця 2.8.1 Визначення коефіцієнта пружності маятника

l0 =

№ m0, кг l , м k, Н/м ε k , %

Таблиця 2.8.2. Визначення основних характеристик вільних та затухаючих коливань пружинного маятника

	m0	=	, l0 =
Число ко-				ω 0 , с-1
ливань	τ , с	T, с	ω , с-1
N

С. зн.	—
	A0=
n A , м	A	, м	λ	β , с-1
0	n
Номер	A	, м		β , с-1
періоду			λ
коливань	n
1
2
3
4

80

81

Лабораторна робота 1.9 Додавання гармонічних коливань

Мета роботи. Оволодіти методами одержання та спостереження складних коливальних процесів на прикладі фігур Ліссажу, набути навичок вимірювання частоти та різниці фаз.

Прилади і матеріали. 1. Осцилограф. 2. Звукові генератори (2 шт.).

Теоретичні відомості Додавання взаємно перпендикулярних коливань. Нехай

тіло бере одночасно участь у двох взаємно перпендикулярних коливальних рухах

						x =	A1 cos(ω t + ϕ 1) ,	(2.9.1)
						y =	A2cоs(ω t + ϕ 2 ) .	(2.9.2)
Знайдемо рівняння траєкторії результуючого руху. Для
цього рівняння приведемо до вигляду:
		x		=		cosω	t cosϕ 1 − sin ω tsin ϕ 1 ,	( 2.9.3)
		A1
		y			=	cosω t cosϕ 2 − sin ω tsin ϕ 2 .		(2.9.4)
		A2

Помножимо перше рівняння на cosϕ2, а друге – на cosϕ 1 і знайдемо їх різницю; потім помножимо перше рівняння на sin ϕ 2 , а друге – на sinϕ 1 і знайдемо їх різницю. Дістанемо

x		cos ϕ 2 −			y			cos ϕ 1 = sin ω t sin(ϕ 2 − ϕ 1) ,	(2.9.5)
A1					A2
	x		sinϕ 2 −		y		sinϕ 1 = cosω t cos(ϕ 2 − ϕ 1 ) .		(2.9.6)
				A2
	A1

Рівняння (2.9.5, 2.9.6) піднесемо до квадрата і почленно додамо їх. В результаті матимемо:

x 2	+	y 2	− 2	xy		cos(ϕ		− ϕ		) = sin2	(ϕ		− ϕ		) .	(2.9.7)
A2		A2		A A			2		1			2		1
1		2		1	2

82

Ми одержали рівняння траєкторії результуючого руху тіла, яке одночасно бере участь у двох взаємно перпендикулярних коливаннях однакових частот. У загальному випадку (2.9.7) є рівнянням еліпса. Проведемо аналіз рівняння (2.9.7):

	а) Різниця фаз ϕ2-ϕ1=0. Рівняння траєкторії:
	Y =	A2	x .	(2.9.8)
		A1

Траєкторія руху тіла – пряма лінія (рис. 2.9.1а).

б) Різниця фаз ϕ2-ϕ1=±π. Рівняння траєкторії
Y = −	A2	x .	(2.9.9)
	A
1

Траєкторія руху тіла – пряма лінія (рис.2.9.1б). в) Різниця фаз ϕ2-ϕ1=±π/2. Рівняння траєкторії:

x 2		y 2
	+		= 1.	(2.9.10)
A2		A2
1		2

Траєкторія руху тіла – еліпс (рис. 2.9.1). Якщо амплітуди складових коливань А1=А2=R, то траєкторія руху – коло

x2 + y2 = R2 .

(2.9.11)

При додаванні двох взаємно перпендикулярних коливань

Y		Y	Y
A2		A2	A2
-A1	A1 X -A1	A1 X -A1	A1 X
-A2		-A2	-A2
a)		б)	в)

Рис.2.9.1. Складання взаємно перпендикулярних коливань

різних частот результуючі рухи тіла відбуватимуться по складних траєкторіях (їх називають фігурами Ліссажу). Вони вписані у прямокутники з сторонами, що відповідають подвійним значенням амплітуд складових коливань.

83

Фігури Ліссажу можна спостерігати за допомогою осцилографа з синусоїдальною розгорткою, для цього слід вимкнути внутрішню розгортку і подати на входи X та Y осцилографа електричні сигнали синусоїдальної форми від двох генераторів (рис. 2.9.2).

Еталонний	Генератор Г2
генератор Г1	(частота невідома)
ν y=ν e	ν x

Рис.2.9.2. Експериментальна установка для калібровки

генератора методом фігур Ліссажу

Плавно змінюючи еталонну частоту, добиваються нерухомої або малорухомої фігури. Якщо вона має вид прямої, еліпса або кола, то частоти коливань однакові: νx=νy.

На

рис.

2.9.3

Рис. 2.9.3. Принцип побудови

осцилограми при складанні взаємно перпендикулярних коливань однакових частот

показано принцип побудови фігури Ліссажу на екрані осцилографа при рівних частотах (цей принцип наочно демонструє

84

Рис. 2.9.4. Фігура Ліссажу

X

O

ny = 6

nx = 4

Y

графічний метод додавання взаємно перпендикулярних коливань). Їх осцилограма являє собою фігуру у вигляді еліпса, форма якого залежить від фазових співвідношень між вхідними напругами i визначається рівняннями (2.9.8-2.9.11).

Якщо осцилограма нерухома, то це свідчить про кратність відношення періодів вхідних сигналів:

	T		n
	y	=	y	,	(2.9.12)
	T		n
	x		x
де nx,ny – цілі числа.
За проміжок часу
τ = nyTx		=	nxTy ,		(2.9.13)

періоди Tx і TY обох сигналів повторюються ціле число разів і повертаються у початкове положення. Для встановлення співвідношення між частотами отриману фігуру потрібно уявно пересікти вертикальною і горизонтальною прямими лініями (рис. 2.9.4) і підрахувати число перетинів

nx і ny віток фігури з ними. Лінії потрібно проводити

так, щоб вони не проходили через точки перетину віток фігури Ліссажу. Відношення цих чисел дорівнює відношенню еталонної і невідомої частот.

Якщо на вхід Y подати еталонну частоту, а на вхід X – невідому, то:

	ν x =	ny	ν y ,	(2.9.14)
		nx

85

а якщо на вхід Y подати невідому частоту, а на вхід X – еталонну, то в рівнянні (2.9.14) значення еталонної частоти слід помножити на nx/ny. Фігури Ліссажу є замкнені криві при кратному відношенню

частот νx/νy і розімкнені – при некратному (рис. 2.9.5).

Замкненні осцилограми нерухомі (стійкі), розімкненні - рухомі (нестійкі). За типом фігури та її положенням відносно системи координат можна знайти співвідношення між фазами, частотами та амплітудами вхідних сигналів. Цей метод вимірювання частоти є одним із найточніших. Похибка вимірювання визначається похибкою установки еталонної частоти і нестабільністю частот обох генераторів. Чим більша нестабільність однієї з цих частот, тим швидше обертається фігура Ліссажу і визначення кратності частот ускладнюється. Осцилографічний метод з синусоїдальною розгорткою доцільно застосовувати при кратності частот ν е / ν х < 10 , оскільки більше число перетинів ліній з фігурою досить важко підрахувати.

Δϕ = 0o	45o	90o	135o	180o	225o	270o	315o
νy:νx							νy:νx
1:1							1:1
1:2							1:2
1:3							1:3
2:3							2:3
Δϕ = 0o	45o	90o	135o	180o	225o	270o	315o

Рис.2.9.5. Фігури Ліссажу.

86

Різницю між фазами вхідних сигналів можна визначити, знаючи положення фігури відносно системи координат (рис. 2.9.6).

Легко показати, що при рівних частотах різниця фаз си-

гналів складає: ϕ

=

A

(2.9.15)

arcsin B

де A – максимальне відхилення

променя по осі Y,

B – відстань

Y

між точками перетину еліпса з

віссю Y.

Додавання

коливань

А

В

X

однакового

напряму.

Биття.

Розглянемо

матеріальну

точку,

яка бере участь у двох однаково

Рис.23.9.6.Визначення різниці

фаз методом фігур Ліссажу.

направлених рухах. Результуюче зміщення точки, що бере участь в кількох коливальних рухах,

становить геометричну суму незалежних зміщень точок, які вона дістає при кожному коливальному русі окремо. Знайдемо рівняння руху тіла, яке бере участь одночасно у двох однаково направлених коливальних рухах з однаковими частотами ω :

y1 =	A1 sin( ω	t +	ϕ 1 ),	(2.9.16)
y2 =	A2 sin( ω	t +	ϕ 2 ).	(2.9.17)

Якщо матеріальна точка одночасно бере участь у двох коливальних рухах, що відбуваються вздовж однієї прямої, то її результуючий рух відбуватиметься також вздовж цієї прямої.

Результуюче зміщення точки у будь-який момент часу дорі-

внює сумі незалежних зміщень
y = y1 + y2 .	(2.9.18)
Зміщення точки, яка бере участь у коливальному русі, від
положення рівноваги дорівнює проекції вектора A (де A –
амплітуда) на вісь OY, який обертається з швидкістю ω	навколо
осі, що проходить через початок системи координат.

87

Оскільки

вектори

A1 і

A2

обертаються

з

Y

однаковою кутовою швидкі-

A

стю

ω (рис. 2.9.7),

то

зсув

фаз між ними

ϕ =

ϕ 2 −

ϕ 1 з

A2

часом не змінюється і вектор

ϕ 2

A1

A

також обертатиметься

з

ϕ

кутовою швидкістю ω .

ϕ 1

X

Рис. 2.9.7. Додавання коливань

Тоді результуюче

ко-

однакового напрямку

ливання буде гармонічним:

y =

A sin( ω

t + ϕ )

(2.9.19)

де А – амплітуда результуючого коливання, ϕ

– початкова фаза.

З рис. 2.9.7 маємо:

A2

= A2 +

A2

+

2A A cos(ϕ

2

− ϕ

1

)

(2.9.20)

1

2

1

2

tgϕ =

A1 sin ϕ 1 +

A2 sin ϕ 2

(2.9. 21)

A1 cosϕ 1 +

A2 cosϕ 2

З (2.9.20) видно, що амплітуда результуючого коливання залежить від амплітуд і різниці початкових фаз складових коливань. Розглянемо випадок додавання однаково напрямлених коливань з різними частотами, рівняння яких

y1 = A1 sin( ω 1 t + ϕ 1 ) ,	(2.9.22)
y2 = A2 sin( ω 2 t + ϕ 2 ).	(2.9.23)
Якщо вектори складових амплітуд A1 і A2	обертатимуться

з різними кутовими швидкостями (рис. 2.9.7), то кут між ними змінюється з часом, і результуюча амплітуда також змінюватиметься з часом, тобто коливання буде негармонійним. Для

простоти припустимо, що A1 = A2 = Ao , ϕ 1 = ϕ 2 = ϕ 0 .

88

x1i і x2i

Тоді
	w	2	- w	1	æ w		2	+ w			ö
y = 2A0 cos					t sinç						1	t + j 0 ÷	.	(2.9.24)
			2					2
					è						ø
Звідси видно, що амплітуда результуючого коливання пері-
одично змінюється за абсолютною величиною з часом
A =			2A cos ω 2 − ω 1 t							.				(2.9.25)
			0		2
Оскільки період модуля косинуса дорівнює π													, то з (2.9.24,

2.9.25) випливає, що період зміни амплітуди коливань складає :

T =			2p		=			1		=	T1 T2		.	(2.9.26)
	w	2	- w	1		n	2	- n	1		T - T	2
											1

Додавання коливань однакового напрямку з близькими частотами називають явищем биття.

При ω 2 − ω 1 < < ω 2 + ω 1 результуючий рух можна роз-

глянути як періодичне коливання з пульсуючою амплітудою, циклічна частота пульсацій якої

ω	=	ω 2 − ω 1	.	(2.9.27)
	2
Частота таких коливань дорівнює середньому арифметичному
значенню частот складових коливань.
Коливальний процес описується рівнянням:
y = A0 cos	ω t sin(ω t + ϕ 0 ) .			(2.9.28)

Явище биття широко застосовують в радіотехніці для порівняння та вимірювання частоти.

Коливання однакового напряму найпростіше додавати графічно (рис. 2.9.8), для цього потрібно побудувати в однаковому масштабі графіки цих коливань, визначивши з них відповідні

зміщення точок від положення рівноваги в момент часу tі.

Алгебраїчно додавши їх, знайдемо зміщення точки результуючого коливання для цього ж моменту часу. Виконавши описану процедуру кілька разів, отримаємо n точок для побудови графіка.

89

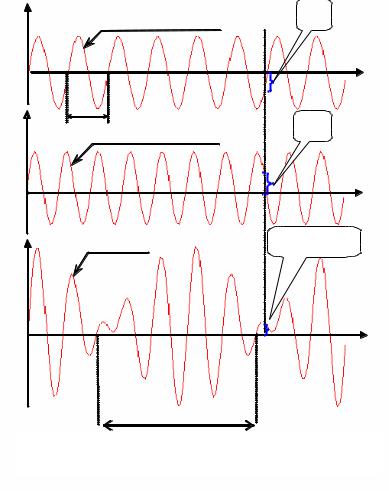
Y	y1 = A sin( ω 1 t + ϕ )

T1

Y	y2 = A sin( ω 2 t + ϕ )

Y	y = y1 + y2

T

y1i

t

y2i

t

yi = y1i + y2i

ti

Рис.2.9.8. Графічний метод додавання однаково

направлених коливань.

Методика виконання роботи та обробка результатів експерименту

1.Зібрати установку (рис. 2.9.3).

2.Ввімкнути генератори та осцилограф, дати їм прогрітися.

90

3. Виставити на досліджуваному генераторі Г2 рукоятку регулятора частоти на позначку “0”. Обертаючи ручку регулятора частоти еталонного генератора Г1, добитися стійкого положення фігури Ліссажу на екрані осцилографа. Занести значення номера позначки N генератора Г2 та значення еталонної частоти νy в таблицю 2.9.1. Схематично перенести малюнок фігури Ліссажу в таблицю. За формулою (2.9.14) знайти невідому частоту νх (рис. 2.9.2, 2.9.4, 2.9.5).

4. Провести аналогічні виміри для решти позначок генератора Г2. Дані занести в таблицю 2.9.1. Побудувати калібровочну криву ν=f(Ν) при N=0...20 для генератора Г2.

5.Подати на входи осцилографа сигнали однакової частоти. Зарисувати на папері в повному масштабі положення еліпса. Визначити різницю фаз між вхідними сигналами (формула 2.9.15, рис. 2.9.6).

6.Не змінюючи вихідні сигнали генераторів за частотою та амплітудою, зібрати установку для спостереження явища биття (рис. 2.9.9). Сигнали від генераторів Г1 та Г2 до входу Y осцилографа обов’язково підводять через ре-

	зистори R1, R2 збері-		Г1	R
	гаючи	полярність
	сигналів. Ввімкнути				Y
	розгортку осцило-		Г2	R
	графа.	Змінити ча-
	стоту	еталонного		Рис. 2.9.9
	генератора на 1...5%.

Змінюючи плавно частоту розгортки осцилографа, добитися стійкої осцилограми та схематично зарисувати її.

Контрольні питання

1. Гармонічні коливання. Графічне зображення та графічний метод додавання гармонічних коливань (с. 68-72, 76-85 ).

91

2.Вільні коливання. Диференційне рівняння вільних коливань. Пружинний, крутильний, фізичний та математичний маятники (с. 68-72).

3.Додавання коливань однакового напрямку. Биття (с. 82-

84).

4.Додавання взаємно перпендикулярних коливань. Фігури Ліссажу (с. 76-81).

					Таблиця 2.9.1
		Результати калібровки генератора.
N	νy, Гц	Фігура Ліссажу	ny	nx	νx, Гц
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

92