Билет 10

Арифметические свойства сходящихся последовательностей.

1. Свойство 1. Если последовательности и сходятся, то сходится последовательность 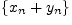и Доказательство. По свойству(Для того чтобы последовательность была сходящейся, необходимо и достаточно, чтобы существовали число и бесконечно малая последовательность такие, что для всех выполнялось равенство);0 по свойству(Сумма и разность бесконечно малых последовательностей есть бесконечно малая последовательность.) 

2. Свойство 2.Если последовательности и сходятся, то сходится последовательность 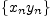и Доказательство.Пусть . Тогда и при . Поэтому В силу свойств бесконечно малых последовательностей

3. Свойство 3.Если последовательности и сходятся к и соответственно, то последовательность сходится к Доказательство.Так как (пусть для определенности ), то посвойству (Если последовательность сходится к числу , то вся последовательность лежит вне окрестности нуля , начиная с некоторого номера.), начиная с некоторого номера . Поэтому определена последовательность и Рассмотрим для номеров цепочку равенств Так как — бмп, а последовательность ограничена, то 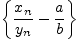- бмп, следовательно последовательность стремится к .

Теоремы о полноте R:

1. Пусть a_n→a ; b_n→b, тогда {a_n+b_n} – сходится. lim (a_n+b_n) = lim a_n + lim b_n. Доказательство: По 3 свойству a_n=a+ α_n, b_n=b+β_n. a_n+b_n=a+α_n+b+β_n = (a+b)+(α_n+β_n). a_n+b_n→α_n+β_n

2. Пусть a_n→a ; b_n→b, тогда {a_n*b_n} – сходится. lim (a_n*b_n) = lim a_n * lim b_n.

3. a_n→a, b_n→b ≠ 0. Тогда {a_n/b_n} – сходится, lim (a_n/b_n) = a/b. Доказательство: По 3 свойству a_n = a+α_n→0, b_n = b+β_n→0. |a_n/b_n – a/b| = |a_nb-b_na|/(b*b_n) = |ab+bα_n–ab–aβ_n|/(b*b/2) = (|bα_n–aβ_n|*2)/b²→0

4. ???

5. , {a_n} – монотонна и ограничена, то. ,a_n↑ и ограничена сверхуM(Mпринадл.R), то:

   1. a_n↑a

   2. a_n≤a≤M, для любогоn

Билет 11

Теорема Кантора о вложенных отрезках.

Пусть задана система вложенных отрезков {Δ_n} = {[a_n, b_n]}, n=1,2,… на , т. е. таких, что и длины отрезков a_n=b_n-a_n→0 при n→+∞. Тогда существует, и притом единственная, точка, одновременно принадлежащая всем отрезкам{Δ_n}.

Д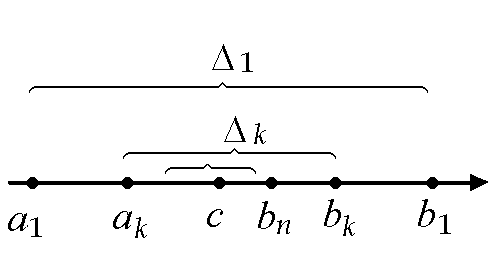оказательство.

Возьмем любое . Ясно, что для любого (из вложенности системы отрезков, см. рис.)

Рассмотрим последовательность левых концов отрезков системы . Она монотонно возрастает и ограничена сверху, например, числом . Тогда, поVсвойству действительных чисел, существует число (точка) такое, что и для любого . В частности, причто означает, что . Так какn было взято произвольным, то точкаc принадлежит всем отрезкам . Найденная точка единственная, так как, если существует и для любого , то для любогоn выполняются неравенства , что противоречит тому, что при .

Замечание 1. , т.е. последовательность левых концов отрезков , возрастая, стремится к точке , а последовательность правых концов отрезков , убывая, стремится к . Действительно,

Замечание 2.Во множестве рациональных чиселтакого свойства, вообще говоря, нет. Например, пусть , а . Ясно, что эта последовательность отрезков удовлетворяет условиям теоремы Кантора, но общая единственная точка — иррациональное число, следовательно, во множестве рациональных чисел общих точек у рассматриваемой системы отрезков нет, т. е.

Замечание 3.То, что в теореме Кантора речь идет о системе отрезков (а, например, не интервалов), существенно. Достаточно рассмотреть систему интервалов Ясно, что в