2.6.2. Анализ устойчивости по расположению корней характеристического уравнения

В разделе 2.1 отмечалось, что характер изменения функции

g(t) =

(и её производных) зависит исключительно характера корней характеристического уравнения системы (2.17) или (2.31). Наглядное представление о характере корней и его влияния на вид функции g=g(t) даёт их расположение на комплексной плоскости. Будут рассматриваться только некратные корни поскольку в дальнейшем будет необходимо обеспечивать условия, при которых система устойчива с некотором запасом. Итак, возможны следующие варианты решения характеристического уравнения.

1. Все корниs_i < 0,i= 1, 2, …,n,вещественные и отрицательные, следовательно, все экспоненты импульсной переходной характеристикиg=g(t) – убывающие функции времени и их сумма в пределе равна нулю.

.Система асимптотически устойчивая.

2. Все корни s_i < 0 ,i= 2, 3, …,n, вещественные и отрицательные, один корень – положительныйs₁ > 0. Эта единственная экспонента с течением времени возрастает и потомуg=g(t) – возрастающая функция времени

.Система неустойчивая.

3. Все корни s_i < 0 ,i= 3, 4, …,n, вещественные и отрицательные, пара комплексно – сопряженных корней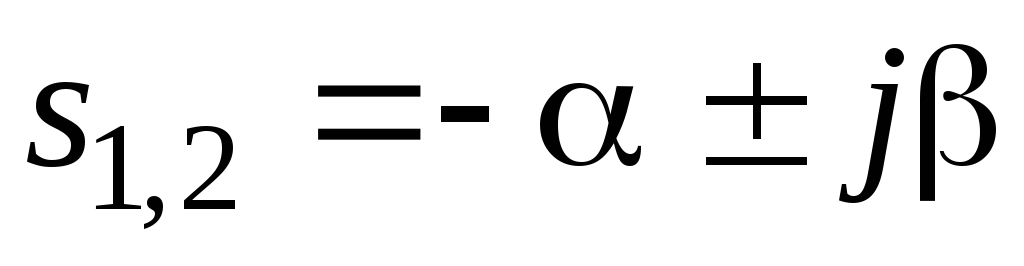,> 0. При изучении импульсной переходной характеристики колебательного звена было показано, что комплексно – сопряженным корням с отрицательной вещественной частью (см. (2.50)) соответствует затухающий колебательный процесс (см. рис. 2.11). Следовательно (с учетом сказанного в пункте 1), функцияg=g(t) в пределе равна нулю

. Система асимптотически устойчивая.

4. Все корниs_i < 0 ,i= 3, 4, …,n, вещественные и отрицательные, пара комплексно – сопряженных корней,> 0 имеет положительную вещественную часть. Этой паре корней соответствует незатухающий колебательный процесс и, следовательно,g=g(t) – возрастающая функция времени

.Система неустойчивая.

Из всего перечисленного вытекают следующие заключения:

• Система устойчива, если все корни её характеристического уравнения имеютотрицательные вещественные части, т.е. находятся в левой полуплоскости комплексной плоскости.Мнимая оськомплексной плоскостиявляется границей устойчивости.

• Система неустойчива, если хотя бы один из корней характеристического уравнения имеет положительную вещественную часть.

• Система находится на апериодической границе устойчивости, если все корни её характеристического уравнения имеют отрицательные вещественные части, а один корень вещественный и равен нулю.

• Система находится на колебательной границе устойчивости, если все корни её характеристического уравнения имеют отрицательные вещественные части, а пара комплексно – сопряженных корней имеет нулевую вещественную часть.

2.6.3. Критерий Михайлова

Итак, расположение корней характеристического уравнения на комплексной плоскости несёт полную информацию об устойчивости системы. Проблема заключается в том, что сложно или невозможно решить аналитически алгебраическое уравнение n– го порядка. Поэтому разработаны методы, позволяющие по косвенным признакам судить об устойчивости, не решая характеристического уравнения. Эти методы называются критериями устойчивости. Ниже будут рассмотрены два частотных критерия: критерий Михайлова и критерий Найквиста.

Пусть s₁,s₂,…,s_n– корни характеристического уравнения системы. Из нихl корней неустойчивых а оставшиесяn-lкорней – устойчивых. Воспользовавшись теоремой Виета, представим характеристическое уравнение в виде

(2.65)

Подставляя в уравнение (2.65) вместо текущей переменной sеё значение s=jω, сформируем комплексный вектор

(2.66)

инайдем изменение фазы этого вектораϕ_Aпри изменении частоты. Но векторпредставляется в (2.66) как произведение векторов разностей, следовательно, изменение фазыϕ_A равно сумме изменений фазы этих векторов разностей. Изображение векторов разностейна комплексной плоскости (см. рис 2.24) позволяет сделать следующее заключение:

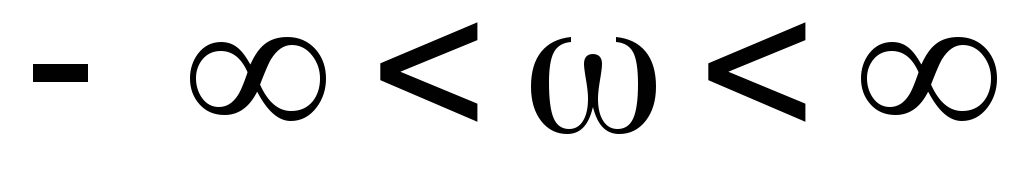• все устойчивые вектора разностей , лежащие в левой полуплоскости, при изменении частоты ω в диапазонеповорачиваются против часовой стрелки на угол, равный 180˚,

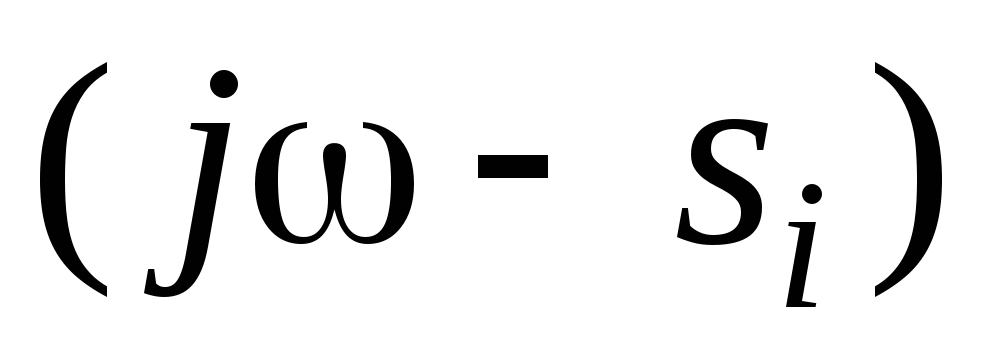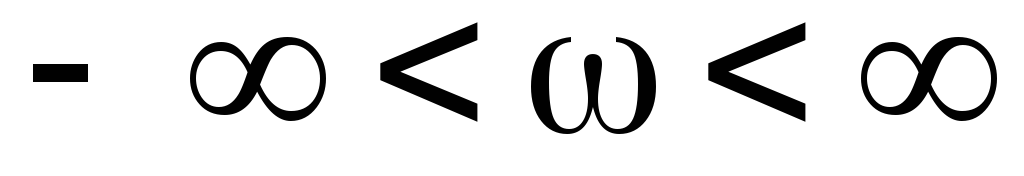• все неустойчивые вектора разностей , лежащие в правой полуплоскости, при изменении частоты ω в диапазонеповорачиваются по часовой стрелке на угол, равный -180˚.

Таким образом,

.

Но, частотные характеристики симметричны относительно точки ω = 0. Поэтому изменение фазы вектора, называемое действительным, определяют при изменении частоты ω в диапазоне

. (2.67)

Если система в замкнутом состоянии устойчива (l = 0), то требуемое значение изменения фазы вектораравно

. (2.68)

Поскольку анализ устойчивости системы проводится в условиях, когда неизвестны значения корней характеристического уравнения, для определения нужно построить годограф вектора, годограф Михайлова, на комплексной плоскости и по нему найти значение.

Итак,

• для того чтобы системав замкнутом состоянии былаустойчивой, необходимо, чтобы

=. (2.69)

Это означает, что годограф Михайлова в положительном направлении (против часовой стрелки) должен обойти nквадрантов, т. е. повернуться на угол, равный,

• система не является устойчивой, если

< . (2.70)

т.е. нарушена последовательность обхода квадрантов,если при ω = 0 годограф Михайлова выходит из начала координат, то система находится на апериодической границе устойчивости,

• если на некоторой частоте годограф Михайлова проходит через начало координат, то система находится на колебательной границе устойчивости.