
- •Радиоавтоматика Учебное пособие
- •Оглавление
- •1 Основные понятия
- •1.1. Система автоматической подстройки частоты
- •1.2.. Система фазовой автоподстройки частоты
- •1.3. Система автоматического сопровождения цели бортовой рлс
- •1.4. Система автоматической регулировки усиления
- •1.5. Система измерения дальности рлс
- •1.6. Обобщенная структурная схема системыРа
- •1.7. Классификация систем ра
- •2. Линейные непрерывные системы автоматическогоуправления
- •2.1. Уравнение состояния системы
- •2.2. Методы линеаризации
- •2.2.1. Линеаризация статической нелинейности
- •2.2.2. Линеаризация динамической нелинейности.
- •2.3. Математические методы описания характеристики линейных непрерывных систем
- •2.3.1. Дифференциальные уравненияn-го порядка
- •2.3.2. Передаточная функция
- •2.3.3. Частотные характеристики
- •2.3.3.1. Комплексный коэффициент передачи
- •2.3.3.2. Амплитудно-фазовая характеристика (афх)
- •2.3.3.3. Логарифмические частотные характеристики (лах)
- •2.3.4. Временные характеристики
- •2.3.4.1. Импульсная переходная характеристика
- •2.3.4.2. Переходная характеристика
- •2.3.5. Методы определения временных характеристик
- •2.3.5.1. Классический метод
- •2.3.5.2. Методы, основанные на использовании преобразования Лапласа
- •2.3.5.3. Моделирование сау
- •2.4 Типовые звенья
- •Идеальное усилительное звено.
- •2.4.2 Идеальное интегрирующее звено.
- •2.4.3 Инерционное звено.
- •2.4.3.1. Комплексный коэффициент передачи звена и его характеристики
- •2.4.3.2. Логарифмические частотные характеристики (лах)
- •2.4.3.3. Временные характеристики инерционного звена
- •2.4.4. Форсирующее звено
- •2.4.4.1. Передаточная функция форсирующего звена
- •2.4.4.2. Комплексный коэффициент передачи звена и его характеристики
- •2.4.5. Сравнение свойств интегрирующего и инерционного звеньев
- •2.4.6. Колебательное звено
- •2.5. Структурные преобразования
- •2.5.1. Стандартные соединения
- •2.5.1.1. Параллельное соединение элементов
- •2.5.1.2. Последовательное соединение элементов
- •2.5.1.3. Встречно – параллельное соединение элементов
- •2.5.2. Система с единичной отрицательной обратной связью
- •2.5.3. Системы с двумя входными воздействиями
- •2.6 Устойчивость линейных непрерывных систем
- •2.6.1. Определение устойчивости
- •2.6.2. Анализ устойчивости по расположению корней характеристического уравнения
- •2.6.3. Критерий Михайлова
- •2.6.4. Критерий Найквиста
- •2.6.4.1.Общий случай критерия Найквиста
- •2.6.4.2. Частный случай. Устойчивые в разомкнутом состоянии системы
- •2.7. Показатели качества линейных непрерывных систем
- •2.7.1. Показатели, определяемые по виду переходной характеристики
- •2.7.2.1. Показатели качества, определяемые по виду амплитудно – частотной характеристики системы в замкнутом состоянии .
- •2.7.2.2. Показатели качества, определяемые по виду логарифмических частотных характеристик
- •2.7.2.3. Показатели качества, определяемые по виду амплитудно – фазовой характеристики системы в разомкнутом состоянии (афх)
- •2.8. Показатели точности в установившемся режиме работы системы
- •2.8.1. Ошибки по регулярному задающему воздействию х(t)
- •2.8.2. Ошибки, вызванные помехойf(t)
- •2.9. Техническое задание, запретные зоны
- •2.9.1. Техническое задание на проектирование системы
- •2.9.2. Построение запретных зон по колебательности
- •2.9.3. Построение запретных зон по точности
- •2.10. Коррекция системы
- •2.10.1. Последовательный корректирующий фильтр
- •2.10.2. Пример коррекции системы
- •2.10.2.1. Построение логарифмических частотных характеристик (лах).
- •2.10.2.2. Построение амплитудно – фазовой характеристики (афх).
- •2.10.2.3. Регулярные ошибки в установившемся режиме
- •2.10.2.4. Случайные ошибки в установившемся режиме
- •2.10.2. Применение последовательного корректирующего фильтра
- •2.10.3. Анализ полученных результатов
- •2.10.3.1. Применение фильтра с опережением по фазе
- •2.10.2.2. Применение фильтра с запаздыванием по фазе
- •3. Системы с прерывистым режимом работы
- •3.1. Импульсные системы радиоавтоматики
- •Контрольные вопросы
- •3.2. Понятие о дискретных функциях и разностных уравнениях
- •Контрольные вопросы
- •3.3. Дискретное преобразование Лапласа иZ- преобразование
- •Изображение часто встречающихся функций времени
- •3.4. Передаточные функции импульсных автоматических систем
- •3.5. Оценка устойчивости импульсной автоматической системы
- •Контрольные вопросы
- •3.6. Качество процессов в линейных импульсных системах
- •Контрольные вопросы
- •3.7. Цифровые системы радиоавтоматики
- •3.8. Цифровая фильтрация
- •Библиографический список
- •1 Основная литература
- •2 Дополнительная литература
3.5. Оценка устойчивости импульсной автоматической системы
Необходимым условием работоспособности импульсной системы является ее устойчивость. Известные из предыдущих бесед основные определения устойчивости непрерывных систем применимы и к импульсным системам, но с учетом ряда особенностей этих систем.
Обратимся к основной формулировке условия устойчивости : импульсная система устойчива, если ее собственное движение с течением времени затухает.
Как уже отмечалось, на практике часто ограничиваются определением дискретной функции Xвых(nT)на выходе системы. Это решение можно получить, например, из формулы (3.17) в виде суммы свободной и вынужденной составляющих:
![]()
Таким образом, условие устойчивости системы следует записать так:
![]()
Оценку устойчивости импульсной системы, как и непрерывной, обычно производят на основании исследования характеристического уравнения замкнутой системы, получаемого из формулы (3.16):
(3.21)![]()
Э![]() то
алгебраическое уравнение имеетт
корнейz, на плоскостиz. Однако, поскольку
переменнаяz появилась
в связи с подстановкой
то
алгебраическое уравнение имеетт
корнейz, на плоскостиz. Однако, поскольку
переменнаяz появилась
в связи с подстановкой![]() ,то каждый кореньZ\
связан с корнямир( на
плоскостир зависимостью
,то каждый кореньZ\
связан с корнямир( на
плоскостир зависимостью
Легко заметить, что нулевому корню, например p1 = О, соответствует кореньZi=1, а корнямpi с отрицательными вещественными частями соответствуют корни : |Zi|<1 .
Теперь можно дать формулировку математического условия устойчивости:
Импульсная автоматическая система устойчива, если все корни ее характеристического уравнения (3.21) лежат внутри круга единичного радиуса, построенного в начале координат комплексной плоскости z (рис. 3.13), точкиz1,z2,z3, z4, z5).
Если хотя бы один из корней лежит на окружности с радиусом R = 1, то система находится на границе устойчивости (рис. 3.13, точкаzб).
При наличии корней |Zi| > 1 система неустойчива (рис. 3.13, точкаz7).

Рис. 3.13. Комплексная плоскость Z
Определение корней характеристического уравнения (3.21) при т≥3 сопряжено с известными трудностями. Поэтому на практике находят применение косвенные оценки — критерии качества, позволяющие оценивать устойчивость импульсных систем без определения корней.
К![]() импульсным системам применим любой из
известных критериев устойчивости
непрерывных систем. Однако для этого
предварительно необходимо произвести
билинейное преобразование полиномаМ
(z) в полиномМ
(ω) по формуле
импульсным системам применим любой из
известных критериев устойчивости
непрерывных систем. Однако для этого
предварительно необходимо произвести
билинейное преобразование полиномаМ
(z) в полиномМ
(ω) по формуле
(3.22)
Такое преобразование позволяет отобразить единичный круг плоскости Z(рис. 3.13) в левую часть комплексной плоскостир, аналогичную области устойчивости непрерывных систем на плоскостир.
К характеристическому уравнению M(ω) = 0, которое также имеет порядокт, применимы алгебраические критерии устойчивости И. А. Вышнеградского и Гурвица. Оценим устойчивость двух конкретных систем.
П![]() ример
1. Импульсная система первого порядка
имеет характеристическое уравнение
ример
1. Импульсная система первого порядка
имеет характеристическое уравнение
П![]() осле
подстановки (22) получим
осле
подстановки (22) получим
и![]() ли
ли
С![]() истема
первого порядка устойчива, если
коэффициенты ее характеристического
уравнения положительны:
истема
первого порядка устойчива, если
коэффициенты ее характеристического
уравнения положительны:
![]()
Исследуем устойчивость импульсной системы с передаточной функцией (3.19).
Х![]() арактеристические
уравнения этой системы
арактеристические
уравнения этой системы
О![]() тсюда
получаем два условия устойчивости:
тсюда
получаем два условия устойчивости:
Второе условие раскрывает важное свойство изучаемого класса систем: устойчивость импульсной системы зависит не только от общего коэффициента передачи в разомкнутом состоянии kv, как это имеет место и в непрерывных системах, но и от периода дискретностиТ : чем большеТ, тем труднее обеспечить устойчивость системы, при неизменномkv.
П![]() ример
2. Характеристическое уравнение импульсной
системы второго порядка
ример
2. Характеристическое уравнение импульсной
системы второго порядка
П![]() осле
перехода к переменной СО получаем
осле
перехода к переменной СО получаем
С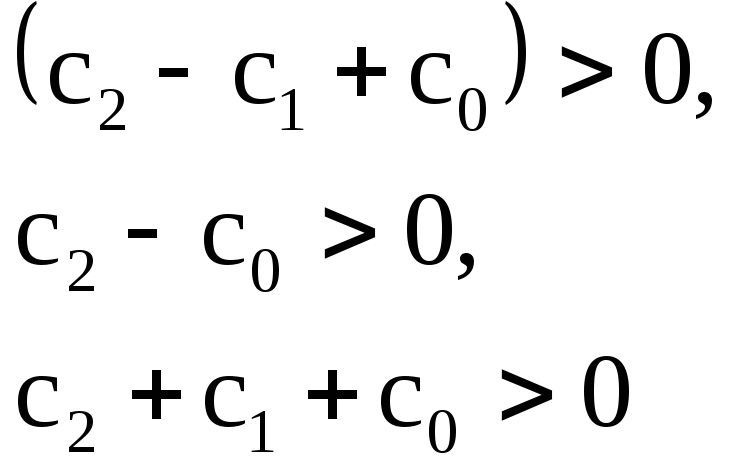 истема
устойчива, если коэффициенты ее
характеристического уравнения
положительны:
истема
устойчива, если коэффициенты ее
характеристического уравнения
положительны:
Эти три неравенства позволяют оценить устойчивость импульсной системы.
Исследование устойчивости систем третьего и более высоких порядков производят с помощью критерия Гурвица.
