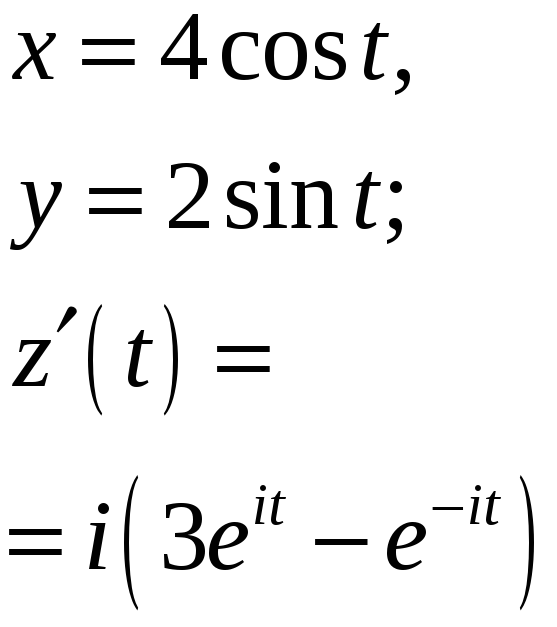3. Комплексные функции действительной переменной
Если
каждому значению действительной
переменной
![]() поставлено в соответствие определенное
комплексное число
поставлено в соответствие определенное
комплексное число
![]() ,
то
,
то
![]() называется комплексной
функцией действительной переменной
называется комплексной
функцией действительной переменной
![]() :
:
![]() .
.
Задание
комплексной функции
![]() равносильно заданию двух действительных
функций
равносильно заданию двух действительных
функций
![]() ,
или заданию вектор - функции
,
или заданию вектор - функции
![]() .
.
Производной
комплексной
функции
![]() называется комплексная функция
называется комплексная функция
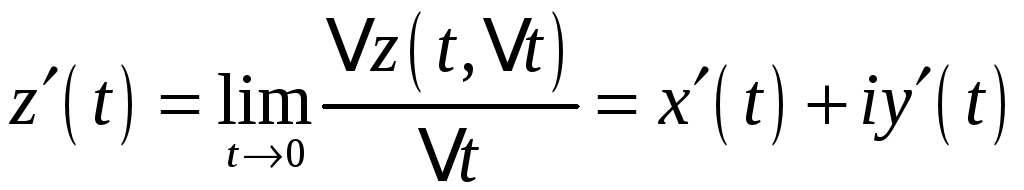
4.Формулы действий с комплексными числами
![]() :
:
![]() ,
,
![]() ;
;
![]()
![]() :
:
![]() ,
,
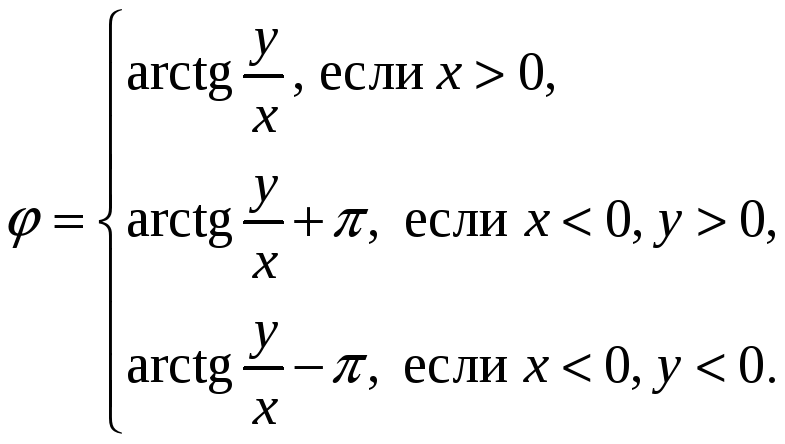
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() :
:
![]() ;
;
![]() ;
;
![]() =
=![]() .
.
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
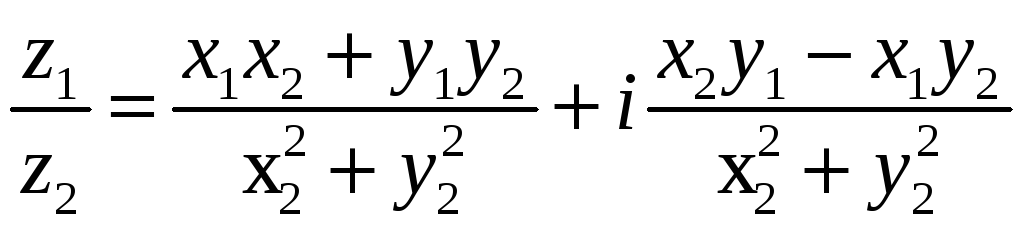 .
.
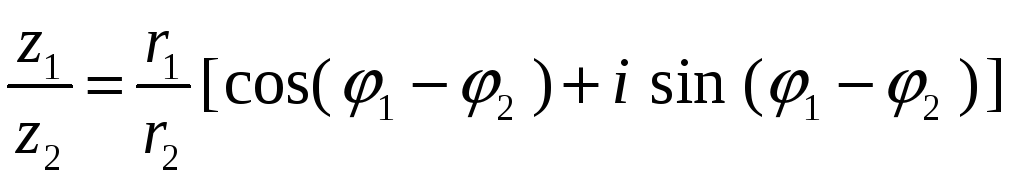 ,
,
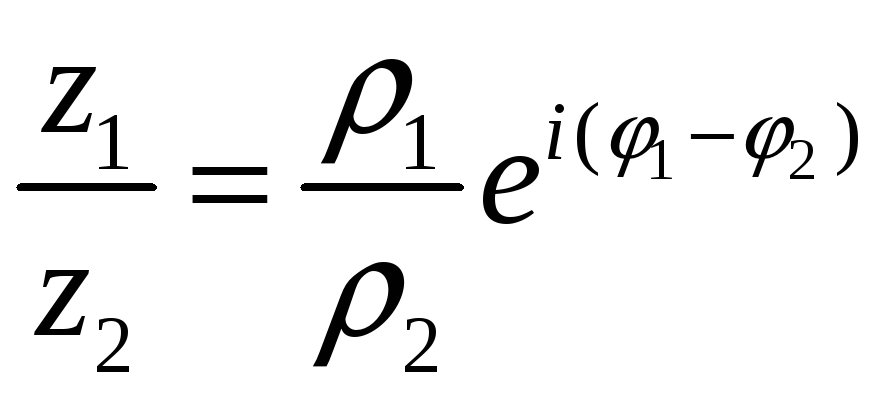 ,
,
![]() ;
;
![]() ,
,
![]() .
.
![]() – формула
Муавра.
– формула
Муавра.
![]() ,
,
![]() ,
k
= 0, 1, 2, …, n
– 1:
,
k
= 0, 1, 2, …, n
– 1:
![]() ,
,
![]() ,
,
![]() ,…….
,…….
![]() .
.
|
ПП 17. 1. Комплексные числа |
|||||||
|
№ п/п |
Задание |
Ответ |
|||||
|
ПП №17.1 |
Вычислите
|
|
|||||
|
ПП №17.2 |
Вычислите
Решение:
|
|
|||||
|
ПП №17.3 |
Вычислите
Решение:
|
|
|||||
|
ПП №17.4 |
Вычислите
|
|
|||||
|
ПП №17.5 |
Вычислите
|
|
|||||
|
ПП №17.6 |
Найдите
Решение:
|
|
|||||
|
ПП №17.7 |
Запишите
число
Решение:
Алгебраическая
форма:
тригонометрическая
форма:
откуда
показательная
форма:
|
|
|||||
|
ПП №17.8 |
Найдите модули и аргументы комплексных чисел:
1)
Решение:
1)
2)
3) |
|
|||||
|
ПП №17.9 |
Запишите комплексные числа
1)
в тригонометрической и показательной форме: Решение:
1)
2)
3)
|
|
|||||
|
ПП №17.10 |
Найдите
Решение:
Тогда
|
|
|||||
|
ПП №17.11 |
Вычислите
Решение:
Представим
число
Тогда по формуле Муавра:
|
64 |
|||||
|
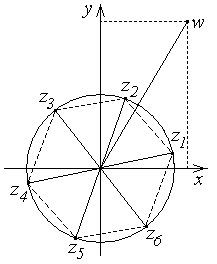
ПП №17.12 |
Вычислите
и изобразите на комплексной плоскости
Решение:
Запишем
число
|
|
|||||
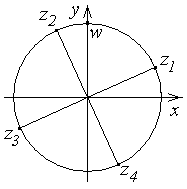
|
ПП №17.13 |
Вычислите
Решение:
Значения корня:
Соответствующие
6 точек располагаются в вершинах
правильного шестиугольника на
окружности радиусом
|
|
|||||
|
ПП №17.14 |
Найдите
все значения
Решение:
Представим
число
При
|
|
|||||
|
ПП №17.15 |
Найдите
все значения корня
Решение:
|
|
|||||
|
ПП №17.16 |
Вычислите
Решение:
|
|
|||||
|
ПП №17.17 |
Вычислите, найдите модуль, аргумент и постройте на комплексной
плоскости
число
Решение: 1)
Для правильного отыскания аргумента рекомендуется изобразить это число на комплексной плоскости.
2)
3)
4)
5)
Вычислим
модуль и аргумент полученного числа:
|
|
|||||
|
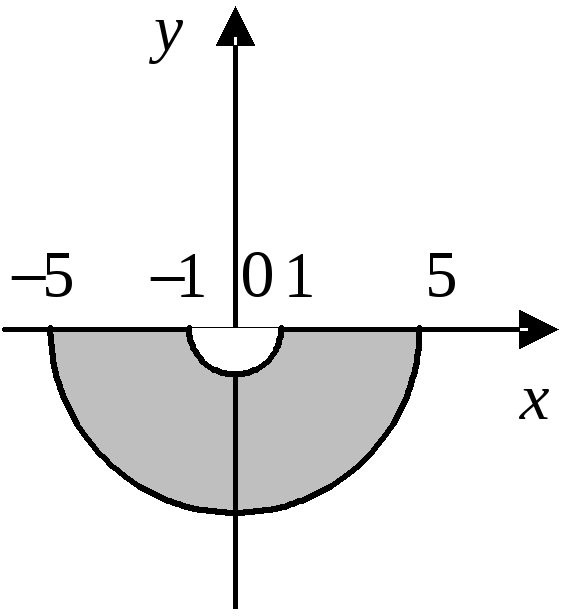
ПП №17.18 |
Дайте
геометрическое описание множества
всех точек комплексной плоскости,
удовлетворяющих условиям:
Решение:
Запишем
Искомое
множество – нижняя половина кольца
с внутренним радиусом
|
|
|||||
|
ПП №17.19 |
Найдите
множество точек комплексной плоскости,
удовлетворяющих уравнению
Решение:
Искомое
множество состоит из точек окружности
единичного радиуса, центр которой
имеет координаты
|
|
|||||
|
ПП №17.20 |
Какие
геометрические образы определяются
условиями
|
|
|||||
|
ПП №17.21 |
Какие
геометрические образы определяются
условиями
|
|
|||||
|
ПП №17.22 |
Какие
геометрические образы определяются
условиями
|
|
|||||
|
ПП №17.23 |
Какие
геометрические образы определяются
условиями
|
|
|||||
|
ПП №17.24 |
Какие
геометрические образы определяются
условиями
|
|
|||||
|
ПП №17.25 |
Дайте
геометрическое описание множеств
всех точек комплексной плоскости,
удовлетворяющих следующим условиям:
|
|
|||||
|
ПП 17. 2. Многочлены в комплексной области |
||
|
№ п/п |
Задание |
Ответ |
|
ПП №17.26 |
Проверьте,
что
Решение:
Так
как
Для
отыскания других корней многочлена
решим уравнение
|
|
|
ПП №17.27 |
Разложите на множители
Решение:
|
|
|
ПП №17.28 |
Разложите
на множители
Решение:
|
|
|
ПП №17.29 |
Разложите
на множители многочлен
Решение:
Очевидно, действительных
корней многочлен не имеет, находим
комплексные корни:
Корни многочлена:
Пары
Аналогично,
Тогда
|
|
|
ПП №17.30 |
Решите
уравнение
Используя
формулу для решения квадратного
уравнения и полагая
|
|
|
ПП №17.31 |
Решите
биквадратное уравнение
Решение:
|
|
|
ПП №17.32 |
Решите
уравнение
Решение:
Введём
подстановку
В
тригонометрической форме
При
При
При
В
тригонометрической форме
При
При
При
|
|
|
ПП №17.33 |
Решите
уравнение
По формуле корней квадратного уравнения
Число,
стоящее под знаком квадратного корня,
можно было бы записать в показательной
форме, а затем по известному правилу
извлечь из него корень. Однако можно
поступить иначе. Положим
Возводим обе части в квадрат и находим
Эта система имеет решения:
|
|
|
ПП 17. 3. КОМПЛЕКСНЫЕ ФУНКЦИИ ДЕЙСТВИТЕЛЬНОЙ ПЕРЕМЕННОЙ |
||
|
№ п/п |
Задание |
Ответ |
|
ПП №17.34 |
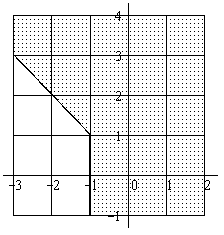
Постройте
кривую, заданную уравнением
Решение:
|
Прямая
|
|
ПП №17.35 |
Постройте
кривую, заданную уравнением
Решение:
|
Арка циклоиды
|
|
ПП №17.36 |
Для
заданной функции
Решение:
Вычислим сумму:
|
|
|
|
Постройте
кривую, заданную уравнением
Решение:
|
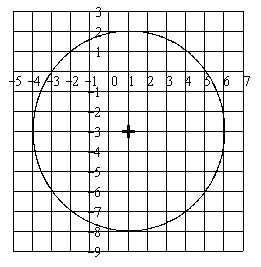
Эллипс
|


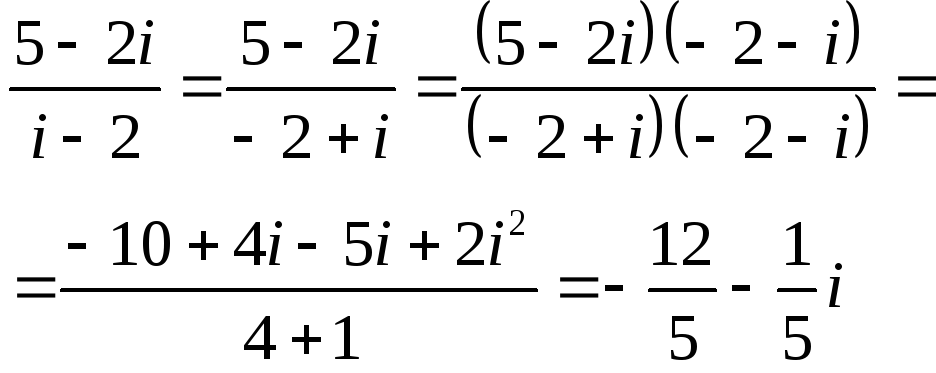
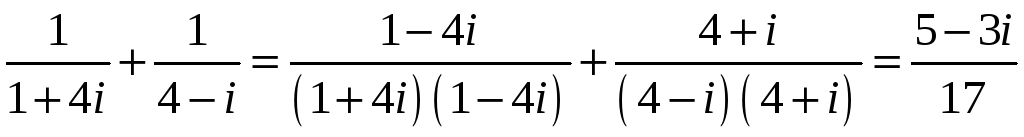 .
. .
Результат представьте в алгебраической
форме.
Решение:
.
Результат представьте в алгебраической
форме.
Решение:
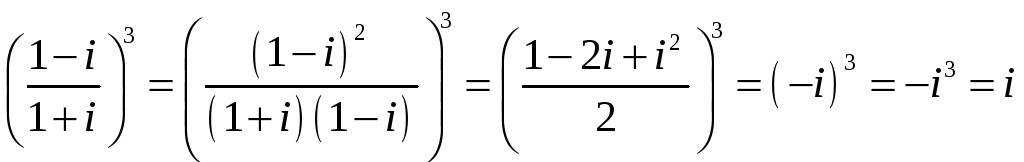 .
.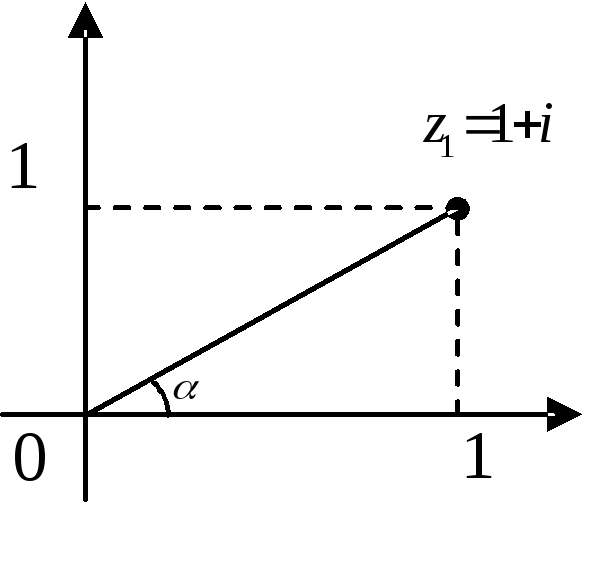
 ;
;
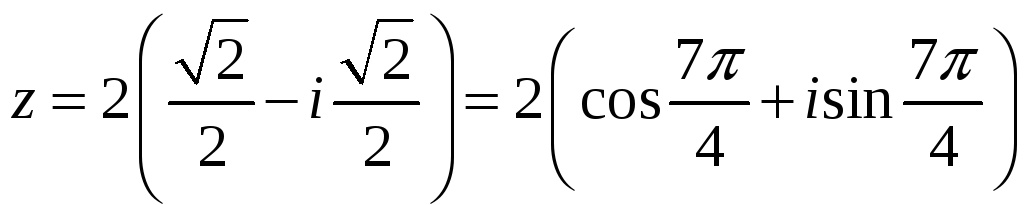 ,
,
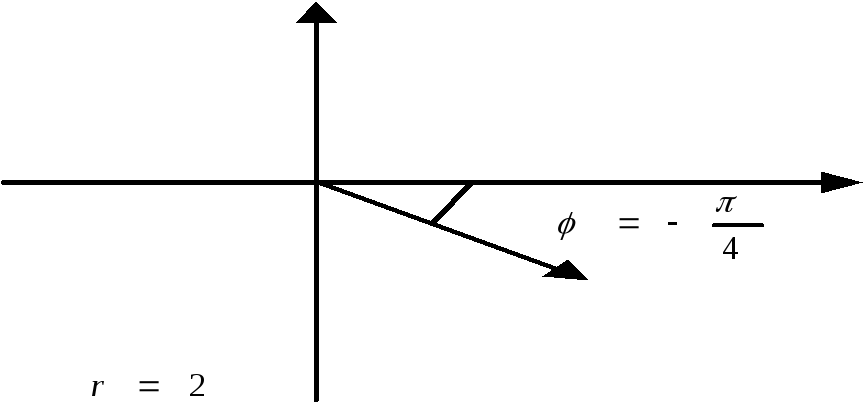 .
.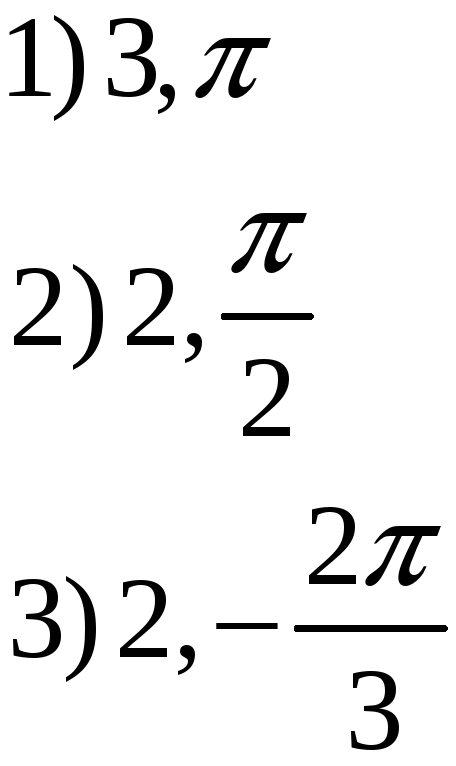
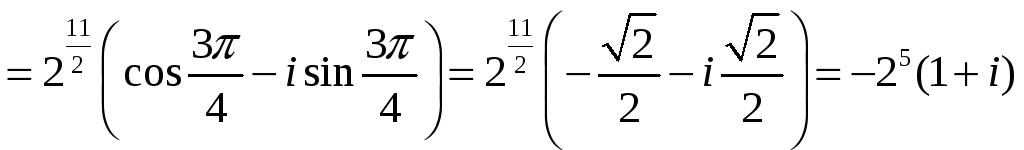 .
.
 .
.
 .
Начальный
аргумент при
.
Начальный
аргумент при
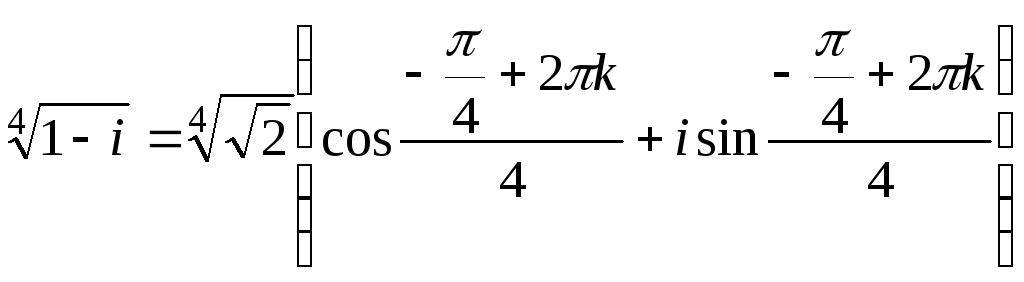
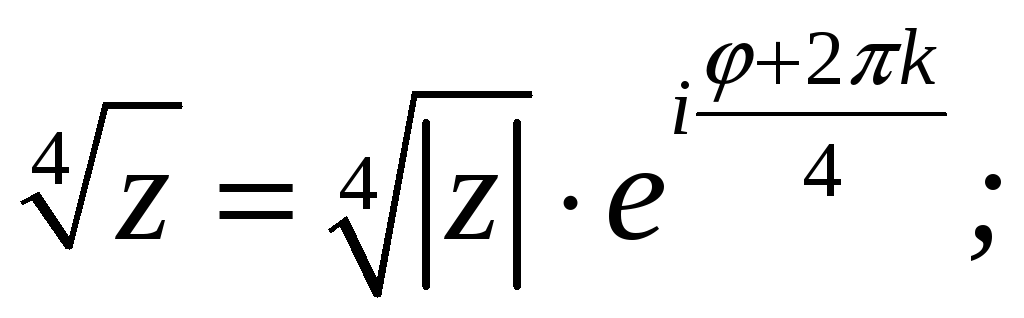 где
где
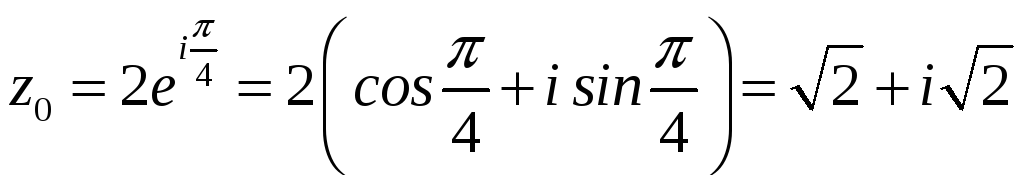 ,
и т.д.
,
и т.д.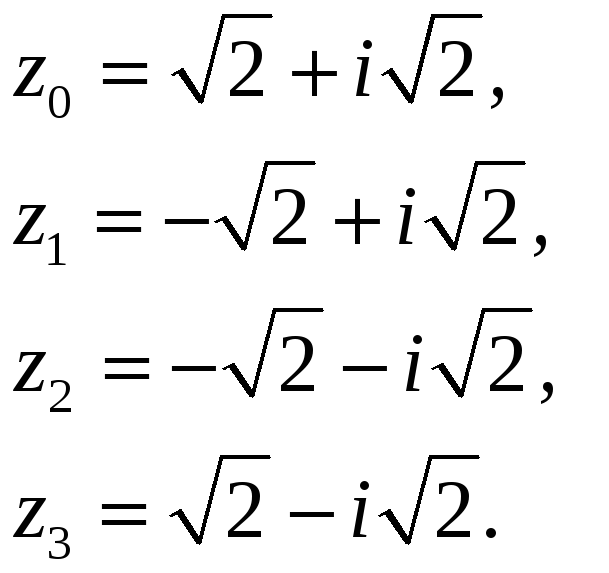
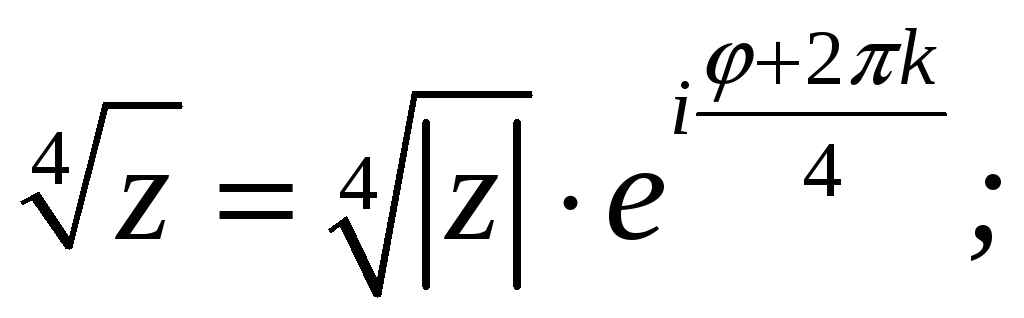 где
где
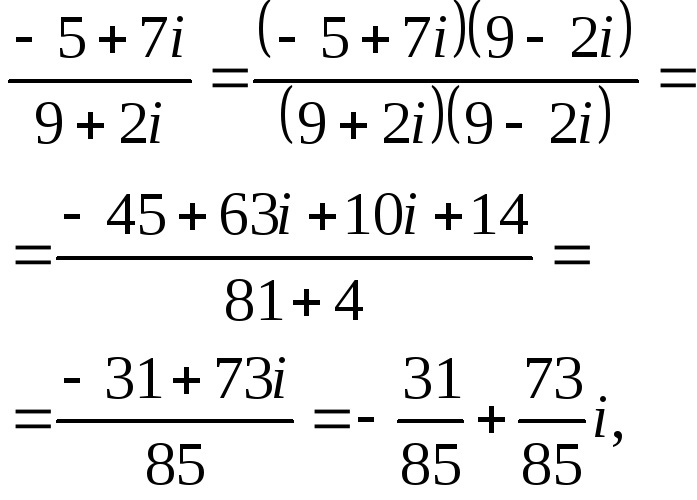 ,
,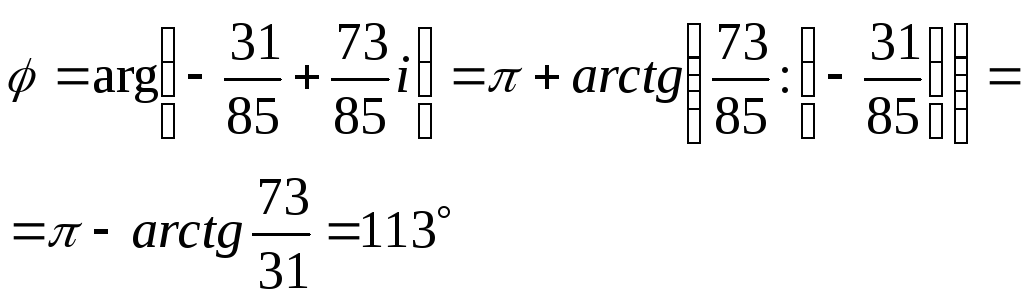 ;
;
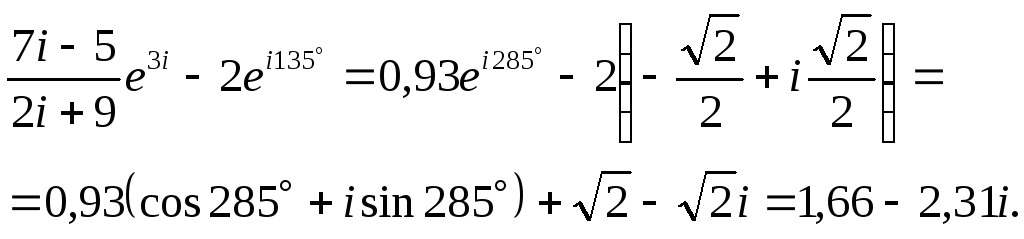
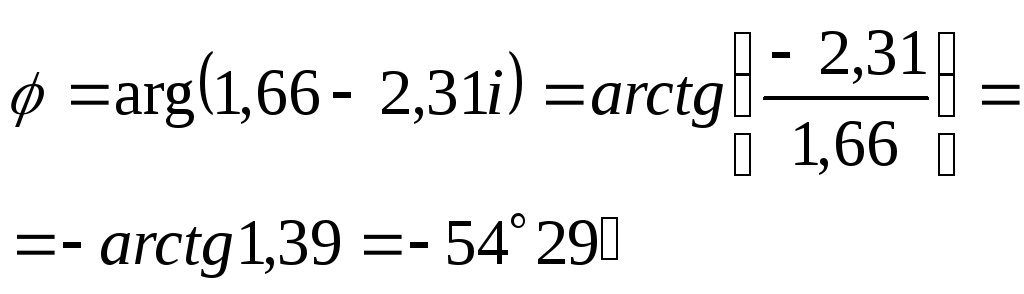 .
.
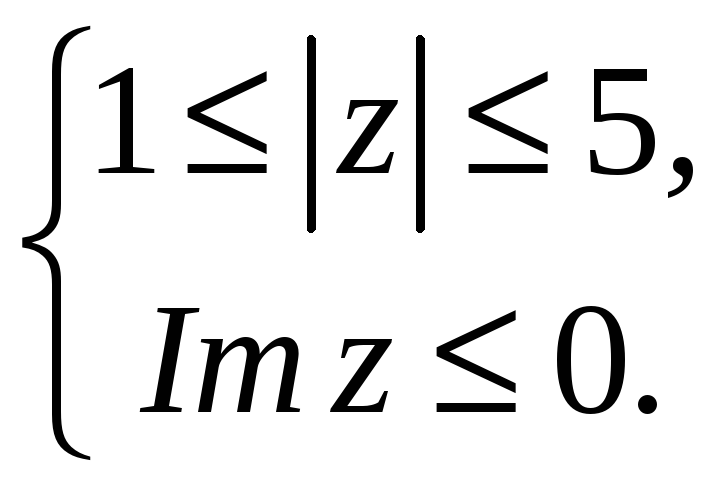
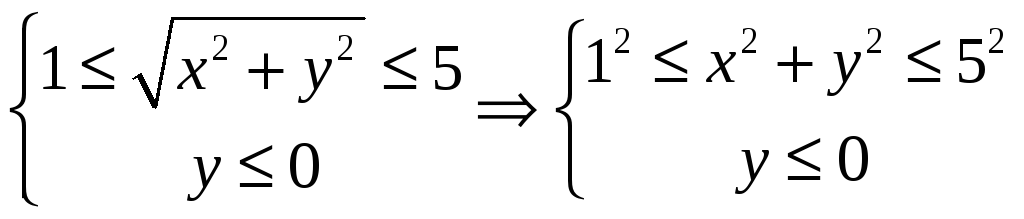 .
.
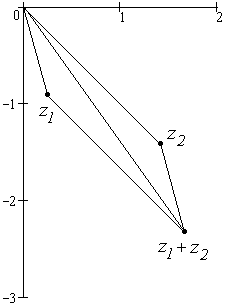
 (см.
рисунок).
(см.
рисунок).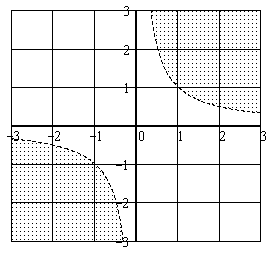 .
(см. рисунок).
.
(см. рисунок).
 (см.
рисунок).
(см.
рисунок).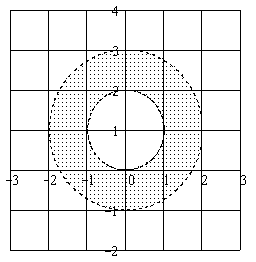 .
(см. рисунок).
.
(см. рисунок).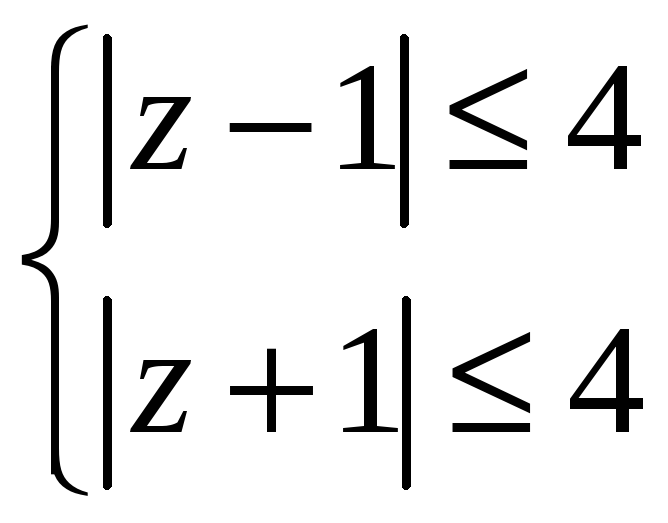 ?
?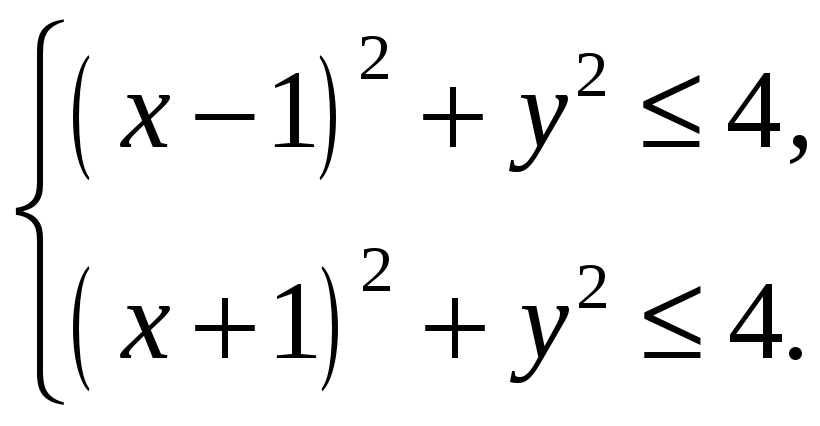
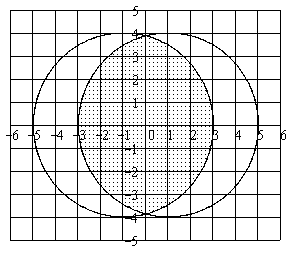 (см.
рисунок).
(см.
рисунок).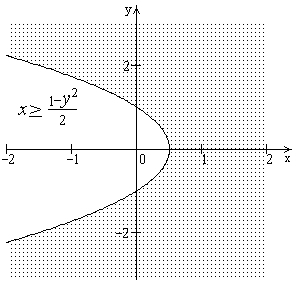
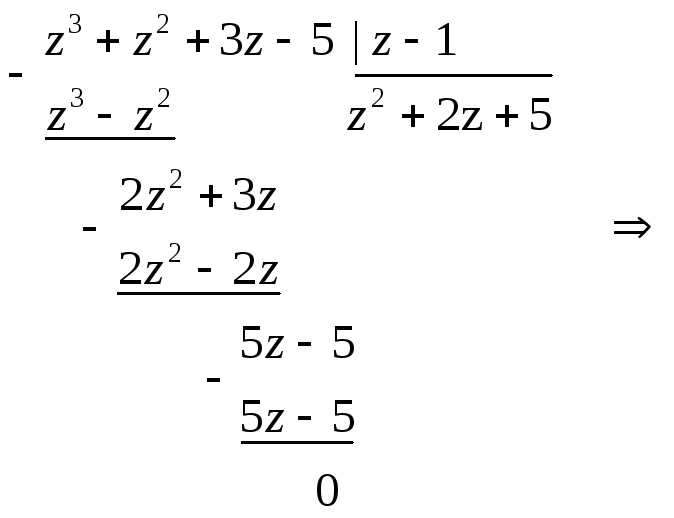
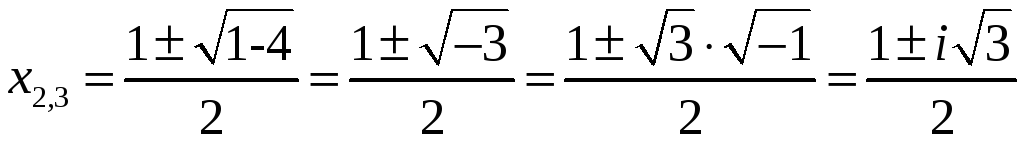 ,
,
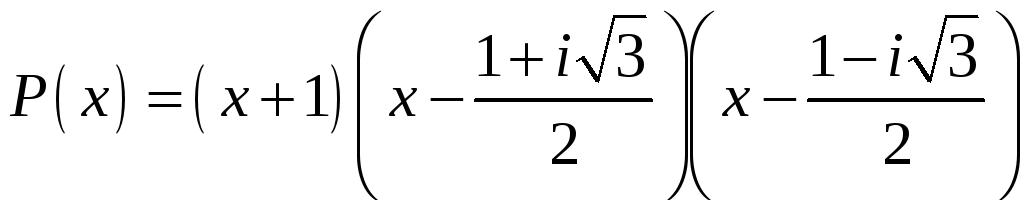 .
.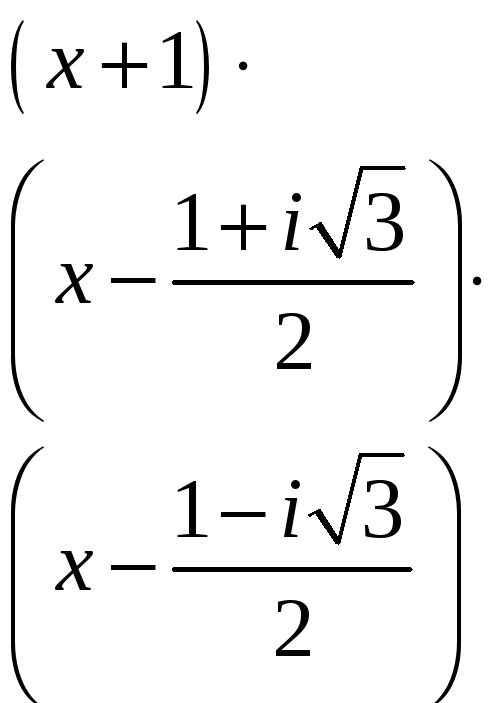
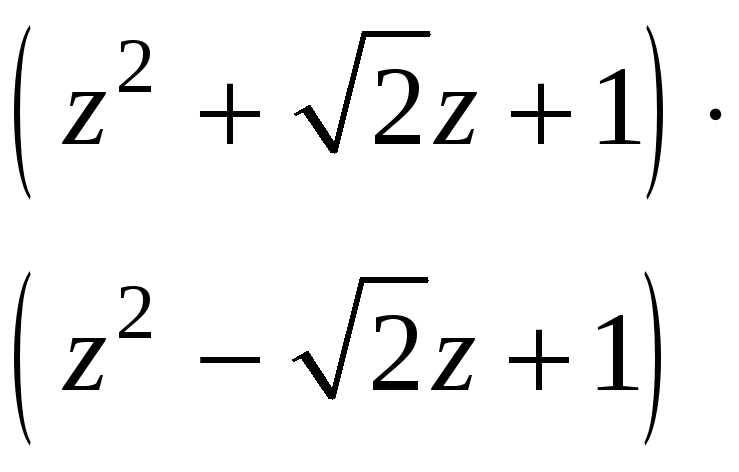
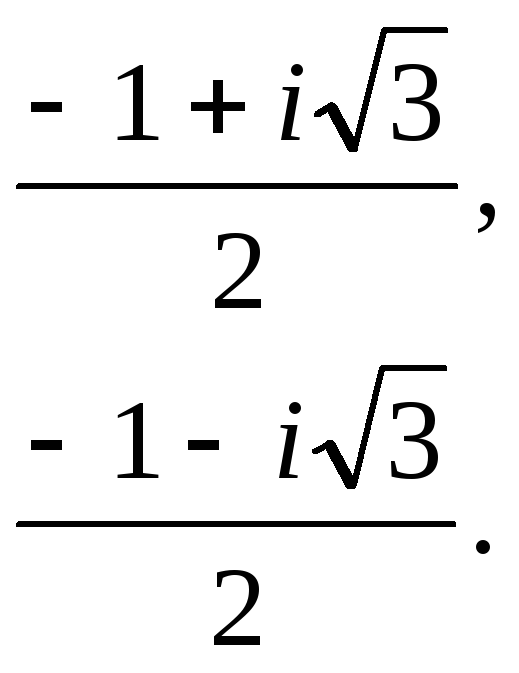
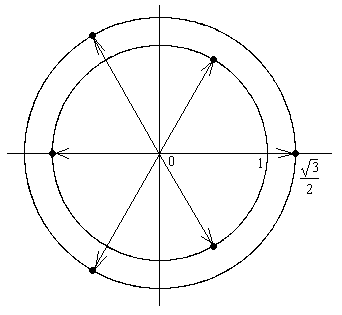
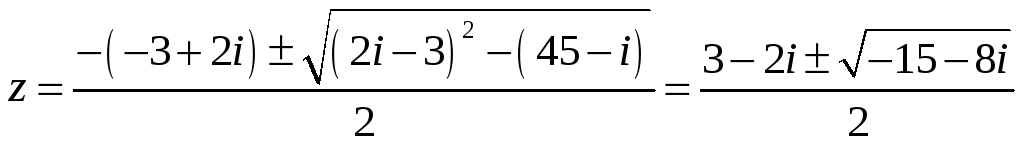 .
.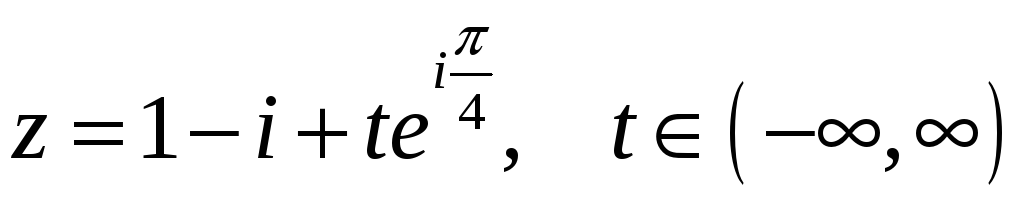 .
.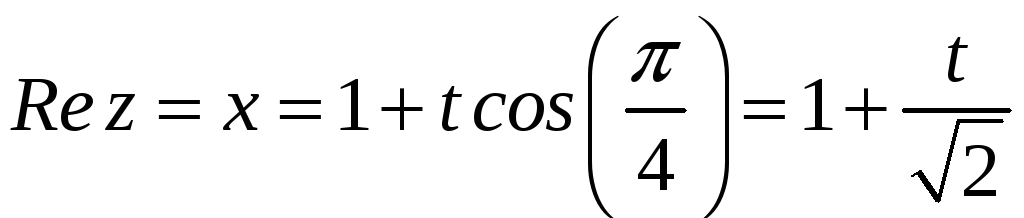 ,
,
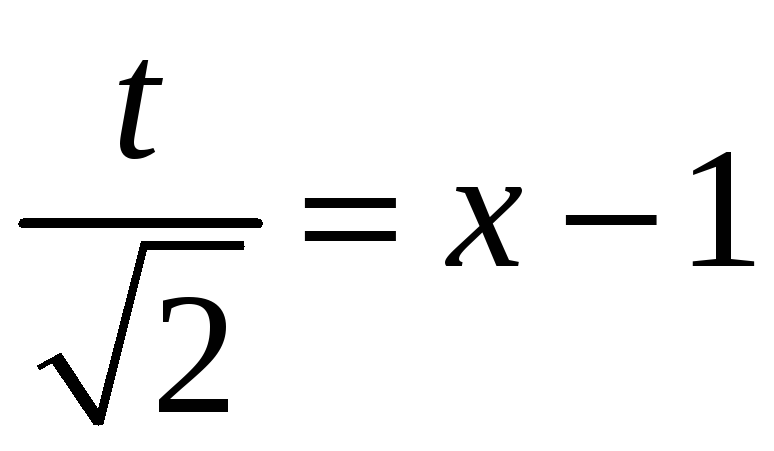 ;
;
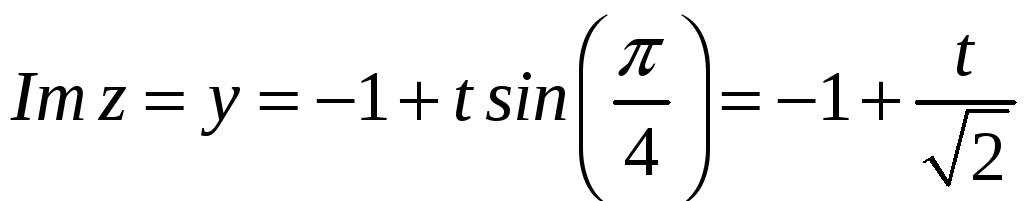 ,
,
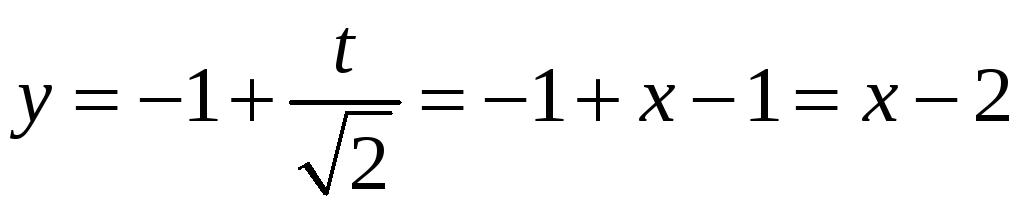 .
.
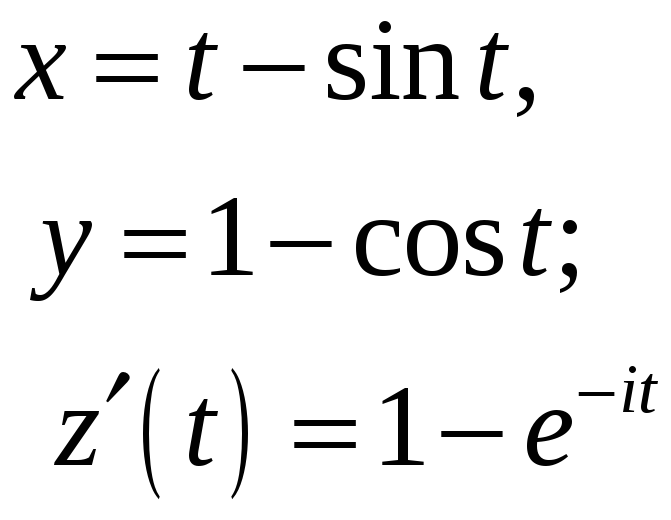

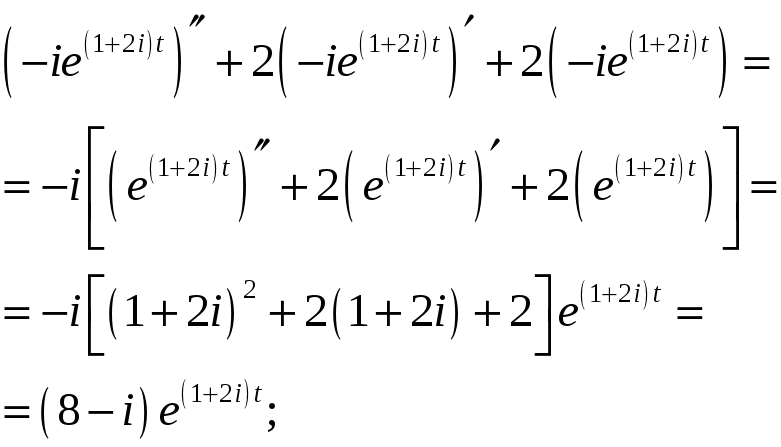
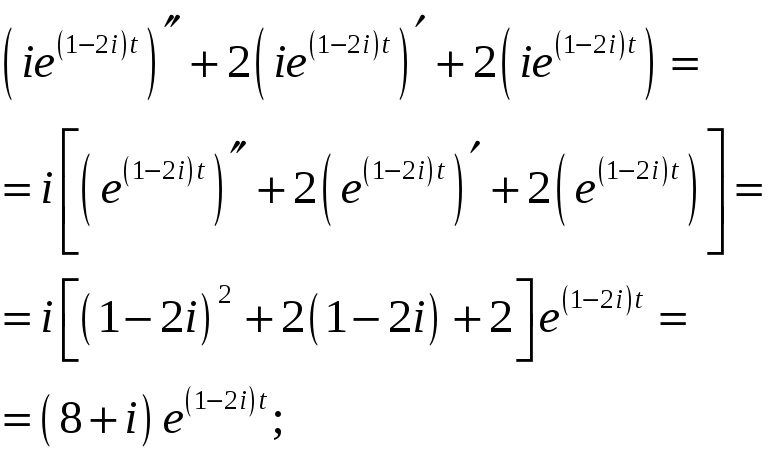
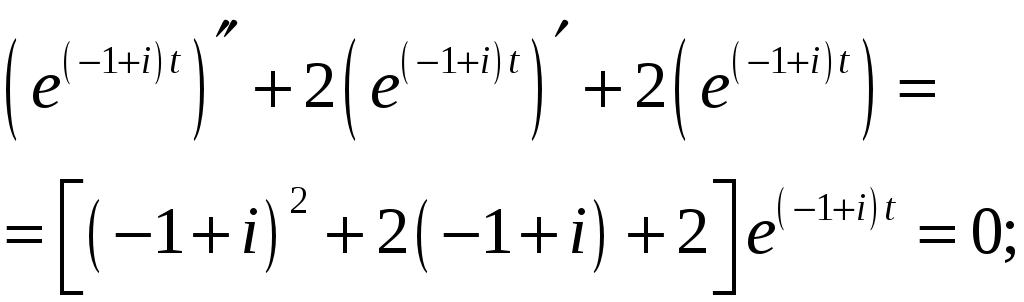
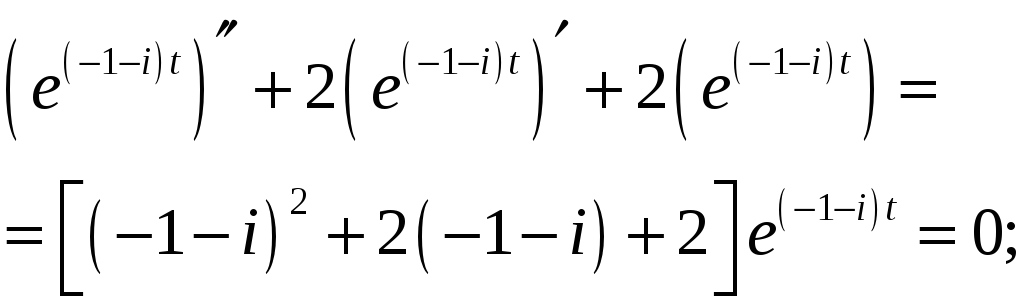
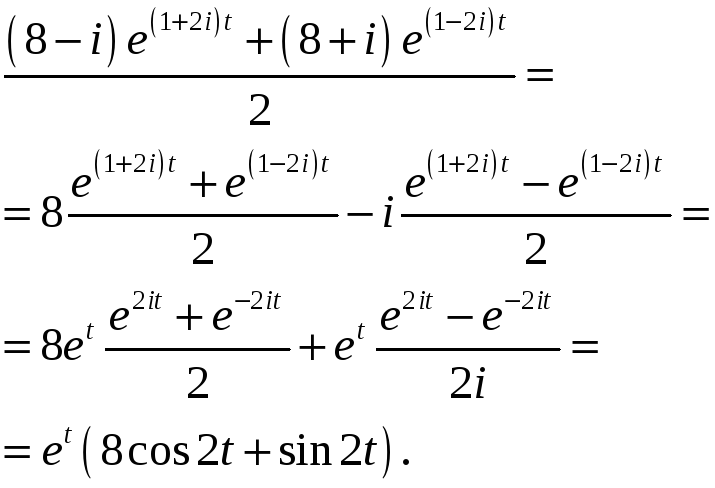
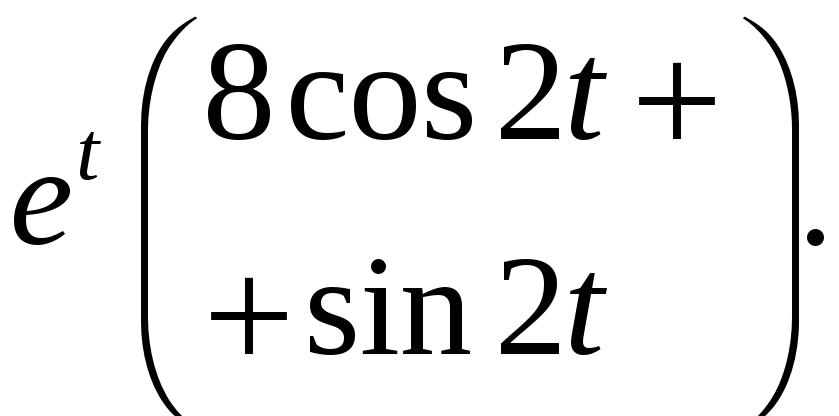
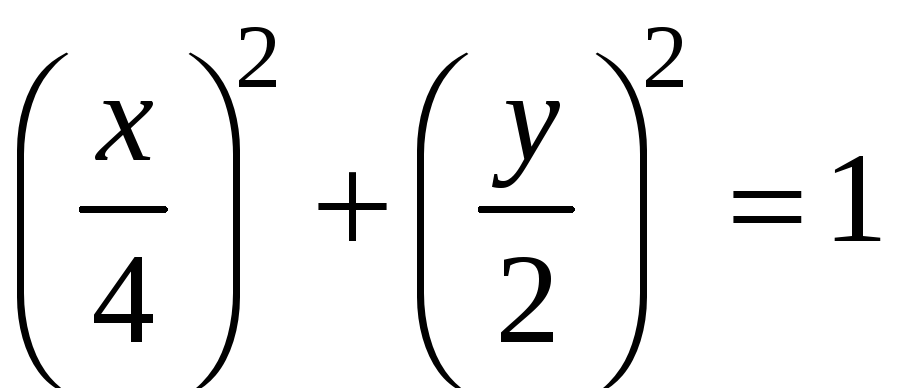 – уравнение эллипса.
– уравнение эллипса.