
- •Точки перегиба
- •Общая схема исследования функции и построения графика
- •Типы задач
- •1. Возрастание и убывание функций
- •2. Экстремумы функции
- •3. Асимптоты графика функции
- •4. Построение графиков функций
- •5. Определение скорости возрастания и убывания функций
- •6. Доказательство неравенств с помощью производной
- •7. Применение производной в теории многочленов для нахождения интервала залегания корней и определения их количества. Связь многочлена со своей производной
- •8. Нахождение наибольшего и наименьшего значения непрерывной функции на отрезке
- •9. Текстовые задачи разного содержания на нахождение наибольшего и наименьшего значения величин
- •II. Кривые, заданные параметрически
- •III. Векторные функции действительной переменной
- •IV. Комплексные функции действительной переменной
7. Применение производной в теории многочленов для нахождения интервала залегания корней и определения их количества. Связь многочлена со своей производной
Если
![]() – корень кратности
– корень кратности![]() многочлена
многочлена![]() ,
то
,
то![]() – корень кратности
– корень кратности![]() его производной.
его производной.
Для
того чтобы найти кратные корни многочлена,
достаточно найти наибольший делитель
многочленов
![]() и
и![]() ,
корни которого будут корнями
,
корни которого будут корнями![]() по крайней мере кратности 2.
по крайней мере кратности 2.
|
№ п/п |
Пример ПП 16 7. Связь многочлена со своей производной |
|
№22 |
Найдите
кратные корни многочлена
Значение
|
8. Нахождение наибольшего и наименьшего значения непрерывной функции на отрезке
Найдите все точки, в которых
 или
или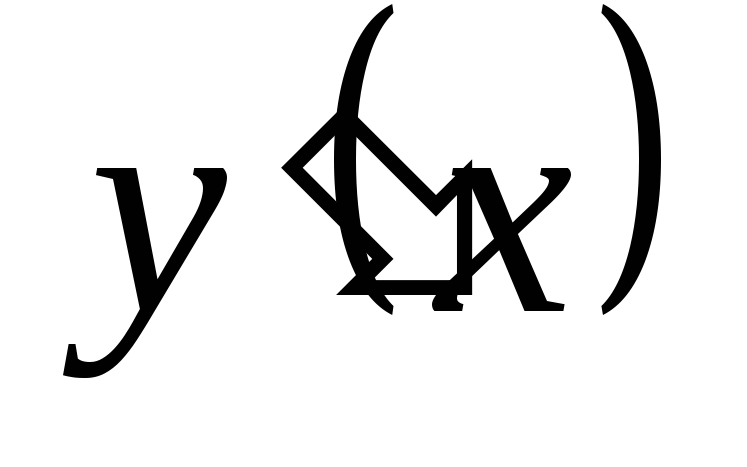 не существует, и отберите из них те, что
лежат внутри
не существует, и отберите из них те, что
лежат внутри .
.Вычислите значения функции в найденных точках и на концах отрезка и выберите из них наибольшее и наименьшее.
|
№ п/п |
Пример ПП 16 8. Нахождение наибольшего и наименьшего значения непрерывной функции на отрезке |
|
№23 |
Найдите
наибольшее и наименьшее значения
функции
Вторая
группа решений является частью первой
и
Сравнивая
их между собой, заключаем, что
|
9. Текстовые задачи разного содержания на нахождение наибольшего и наименьшего значения величин
|
№ п/п |
Примеры ПП 16 9. Текстовые задачи разного содержания на нахождение наибольшего и наименьшего значения величин
|
|
№24 |
Обозначим
высоту цилиндра
Из
|
|
№25 |
Владелец
фабрики установил, что если он будет
продавать свои изделия по цене
|
|
пп 16. I. исследование функций | |||||||||||||||||||||||||||||||||
|
№ п/п |
ЗАДАЧИ | ||||||||||||||||||||||||||||||||
|
ПП16.I №1 |
Найдите
интервалы монотонности и точки
экстремума функции
РЕШЕНИЕ:
Функция
Функция
| ||||||||||||||||||||||||||||||||
|
ПП16.I №2 |
Найдите
экстремумы функции
Вид
графика функции
| ||||||||||||||||||||||||||||||||
|
ПП16.I №3 |
Исследуйте
функцию
Р
Функция
обращается
в ноль при
| ||||||||||||||||||||||||||||||||
|
ПП16.I №4 |
Исследуйте
функцию
РЕШЕНИЕ:
Производная
функции
второй
множитель положителен при любых
Знак
производной совпадает со знаком
при
в
точках
а
в точках
| ||||||||||||||||||||||||||||||||
|
ПП16.I №5 |
Исследуйте
функцию
РЕШЕНИЕ: Производная функции представляет собой многочлен, который мы преобразуем следующим образом:
| ||||||||||||||||||||||||||||||||
|
ПП16.I №6 |
Исследуйте
функцию
РЕШЕНИЕ:
Вид
графика функции
| ||||||||||||||||||||||||||||||||
|
ПП16.I №7 |
Сколько
раз график функции
РЕШЕНИЕ:
Функция
определена для всех
не обладает определенной четностью, непериодическая.
График
функции
Построим схему.
| ||||||||||||||||||||||||
|
ПП16.I №8 |
Исследуйте
функцию
РЕШЕНИЕ:
1)
Область определения функции:
2
3)
Точка пересечения с осью
| ||||||||||||||||||||||||
|
ПП16.I №9 |
Исследуйте
функцию
РЕШЕНИЕ:
1)
Функция определена всюду, кроме точки
График
функции имеет вертикальную асимптоту
2)
Точка пересечения с осями:
3) Выясним, существуют ли наклонные асимптоты. Вычислим пределы:
4)
Находим производную:
5)
Находим вторую производную
В
области определения функции
График
| ||||||||||||||||||||||||||||||||||||||||
|
ПП16.I №10 |
Исследуйте
функцию
РЕШЕНИЕ:
В
области определения функции
График
| ||||||||||||||||||||||||||||||||||||||||
|
ПП16.I №11 |
Исследуйте
функцию
РЕШЕНИЕ:
График
| ||||||||||||||||||||||||||||||||||||||||
|
ПП16.I №12 |
Постройте
график функции
Область
определения функции:
П
| ||||||||||||||||||||||||||||||||||||||||
|
ПП16.I №13 |
Найдите
область определения функции (ООФ)
РЕШЕНИЕ: ООФ
Введем
переменную
Из
двух последних неравенств следует,
что
Итак,
функция
Область
определения функции найдем из
неравенства
| ||||||||||||||||||
|
ПП16.I №14 |
Д РЕШЕНИЕ: Рассмотрим
функцию
| ||||||||||||||||||
|
ПП16.I №15 |
Найдите
интервал, в котором находятся корни
многочлена
РЕШЕНИЕ:
Полученный
квадратный трехчлен имеет положительный
коэффициент у старшего члена (на
графике ветви параболы направлены
вверх) и отрицательный дискриминант
(график не имеет точек пересечения с
осью
И | ||||||||||||||||||
|
ПП16.I №16 |
При
каких значениях
РЕШЕНИЕ:
Рассмотрим
функции
И | ||||||||||||||||||
|
ПП16.I №17 |
Для
каждого действительного числа
РЕШЕНИЕ:
В При
| ||||||||||||||||||
|
ПП16.I №18 |
Найдите
число корней уравнения
РЕШЕНИЕ:
Г
Аналогично
для касательной
В
итоге получаем, что при
| ||||||||||||||||||
|
ПП16.I №19 |
Найдите
наибольшее и наименьшее значения
функции
РЕШЕНИЕ:
Из
условия
тогда
Критические
точки находим из условия
Отрезку
| ||||||||||||||||||
|
ПП16.I №20 |
Для
каждого значения параметра
РЕШЕНИЕ:
| ||||||||||||||||||
|
ПП16.I №21 |
При
каких значениях
РЕШЕНИЕ: Производная
обращается
в ноль при
| ||||||||||||||||||
|
ПП16.I №22 |
Найдите число, куб которого превышает утроенный его квадрат на минимальное значение. РЕШЕНИЕ:
Обозначим
через
Производная
| ||||||||||||||||||
|
ПП16.I №23 |
В арифметической прогрессии шестой член равен 3, а разность прогрессии больше 0,5. При каком значении разности этой прогрессии произведение первого, четвертого и пятого ее членов является наибольшим? РЕШЕНИЕ:
По
условию
Найдем
значение
Наибольшего
значения функция
| ||||||||||||||||||
|
ПП16.I №24 |
Величина
угла при основании равнобедренного
треугольника равна
РЕШЕНИЕ:
По
условию
О В
Введем функцию
Отношение
| ||||||||||||||||||
|
ПП16.I №25 |
Прямой круговой конус с наибольшим объемом вписан в данный конус так, что вершина внутреннего конуса находится в центре основания данного конуса. Докажите, что высота внутреннего конуса составляет одну треть высоты данного конуса. РЕШЕНИЕ:
Обозначим
S1
Вблизи
| ||||||||||||||||||
|
ПП16.I №26 |
Шоссе пересекает местность с запада на восток. В 9 км к северу от шоссе находится лагерь, а в 15 км к востоку от ближайшей на шоссе к лагерю точки расположен город. Каков должен быть маршрут, чтобы добраться в город в кратчайший срок, если скорость движения по полю 8 км/час, а по шоссе – 10 км/час? РЕШЕНИЕ:
Пусть
лагерь располагается в точке
О
Время
движения определяется функцией
| ||||||||||||||||||
|
ПП16.I №27 |
По
двум взаимно перпендикулярным дорогам
по направлению к перекрестку движутся
две автомашины со скоростями
Р
Пусть
первая и вторая машины в начальный
момент времени находятся в точках
Квадрат
расстояния между машинами определяется
функцией
| ||||||||||||||||||
|
ПП16.I №28 |
Автомобиль
выезжает из пункта А и едет с постоянной
скоростью
РЕШЕНИЕ:
Вычислим
время, которое затрачивает автомобиль
на весь путь от А до остановки и обратно:
Производная
| ||||||||||||||||||
|
ПП16.I №29 |
Требуется
построить несколько одинаковых домов
с общей площадью 40000 м2.
Затраты на постройку одного дома,
имеющего
РЕШЕНИЕ:
Обозначим
через
где
Производная
Исследуя
знак производной, можно показать, что
эта точка является точкой минимума
| ||||||||||||||||||
|
ПП16.I №30 |
Между
двумя портами, удаленными друг от
друга на расстояние 1200 км, с постоянной
скоростью курсирует теплоход. Затраты
на рейс в одном направлении слагаются
из двух частей. Первая часть, связанная
с обслуживанием пассажиров,
пропорциональна времени нахождения
в пути, другая, обусловленная стоимостью
топлива, пропорциональна кубу скорости
движения. Найти скорость, с которой
должен идти теплоход, чтобы затраты
на рейс были минимальны, если известно,
что при скорости 90 км/час затраты равны
11,61 тысяч рублей, причем стоимость
обслуживания пассажиров составляет
РЕШЕНИЕ:
Пусть
Производная
при
Исследуя
знак производной, можно показать, что
при
| ||||||||||||||||||
|
ПП16.I №31 |
Три
бригады должны выполнить работу.
Первая бригада делает в день 200 деталей,
вторая – на
По
условию вторая бригада делает в день
Производная
при
Исследуя
знак производной, можно убедиться,
что при
| ||||||||||||||||||

 .
. Площадь
поверхности сферы равна
Площадь
поверхности сферы равна



 ,
,
 ,
,
 ЕШЕНИЕ:
ЕШЕНИЕ: ,
,

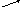


 )
Функция нечетная:
)
Функция нечетная: и постройте её график.
и постройте её график. ;
;

 .
Знак производной определяется знаком
дроби
.
Знак производной определяется знаком
дроби При переходе через другую критическую
точку
При переходе через другую критическую
точку .
Видим, что
.
Видим, что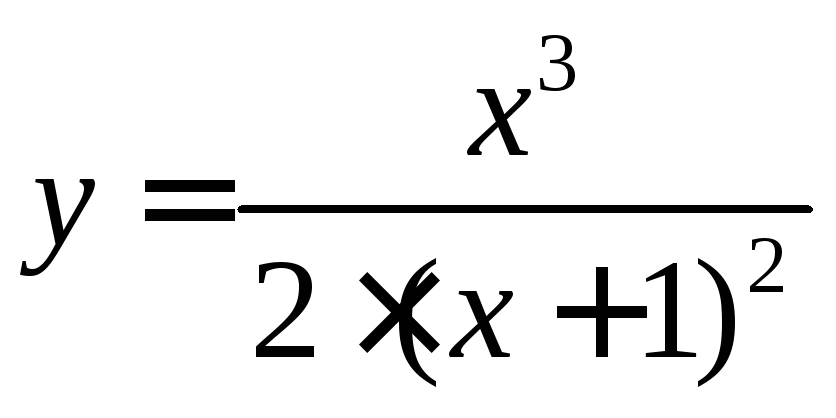 имеет
вид
имеет
вид
 и постройте её график.
и постройте её график.
 ,
т.е.,
,
т.е., .
Знак производной определяется знаком
.
Знак производной определяется знаком .
При переходе через критическую точку
.
При переходе через критическую точку .
Видим, что
.
Видим, что
 .
Для
.
Для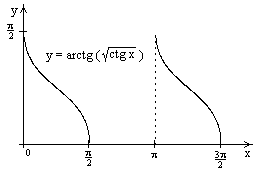 айдем
вторую производную
айдем
вторую производную .
Корень уравнения
.
Корень уравнения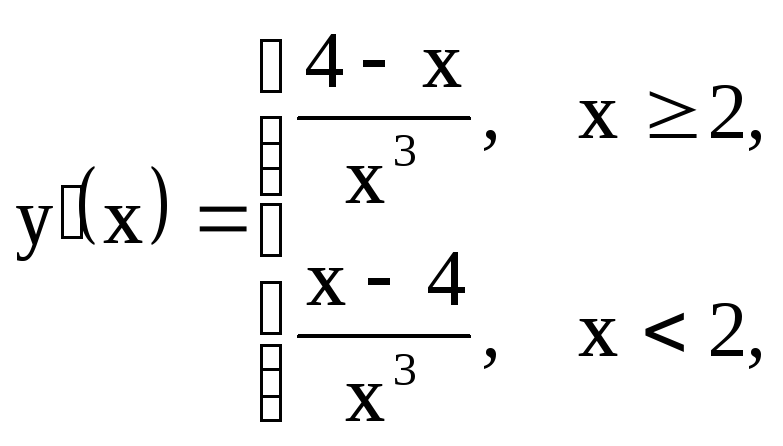
 остроим
схему.
остроим
схему.





 окажите,
что
окажите,
что .
. з
этого следует, что
з
этого следует, что сследуем
поведение
сследуем
поведение ычислим
ычислим рафик
функции
рафик
функции


 ,
точка
,
точка
 если
если
 если
если



 бозначим
бозначим


 ,
,
 бозначим
расстояние
бозначим
расстояние ЕШЕНИЕ:
ЕШЕНИЕ:
 ;
;

