§ 8. Погрешность простейших формул численного дифференцирования

Первая формула (2)

или .

Для оценки погрешности воспользуемся разложением по формуле Тейлора:

, где .

 .

 —погрешность формулы (2).

Вторая формула (3)

или .

Для оценки погрешности также воспользуемся разложением по формуле Тейлора:

, где ,

, где .

Вычтем из первой строки вторую и поделим на 2h:

.

Поскольку , существует точка, такая что(предполагая непрерывность третьей производной).

 —погрешность формулы (3).

Третья формула (4)

или .

Для оценки погрешности также воспользуемся разложением по формуле Тейлора:

, где ,

, где .

Сложим строки и поделим на h²:

.

Существует точка , такая что(предполагая непрерывность четвертой производной).

 —погрешность

формулы (4).

Замечание: говорят, что первая погрешность имеет порядок h, а вторая и третья — порядок h².

§ 9. Разделенные разности. Многочлен Ньютона.

Вступление: схема Эйткена, формулы вычисления производных, используют разности значений функций, деленные на расстояния между узлами. Похожие формулы называют разностными методами.

Опр. Назовем разделенными разностями 0-го порядка значения f(x_i).

Назовем разделенными разностями 1-го порядка:

.

Назовем разделенными разностями 2-го порядка:

.

Назовем разделенными разностями порядка l:

.

Для вычисления всех разделенных разностей используют таблицу, как в схеме Эйткена:

f(x0)
	f(x0; x1)
f(x1)		f(x0; x1; x2)
	f(x1; x2)
f(x2)				f(x0; ...; xn)
	
		f(xn–2; xn-1; xn)
	f(xn–1; xn)
f(xn)

Лемма 1.(без док-ва)

.

Опр. Интерполяционным многочленом Ньютона с разделенными разностями называется

.

Теорема 2.

Многочлен Ньютона совпадает с многочленом Лагранжа.

Док-во:

1)

где L_k(x) — многочлен Лагранжа степени k по узлам x₀,...,x_k.

2) .

3) Покажем, что для любого k выполняется .

По определению многочлена Лагранжа

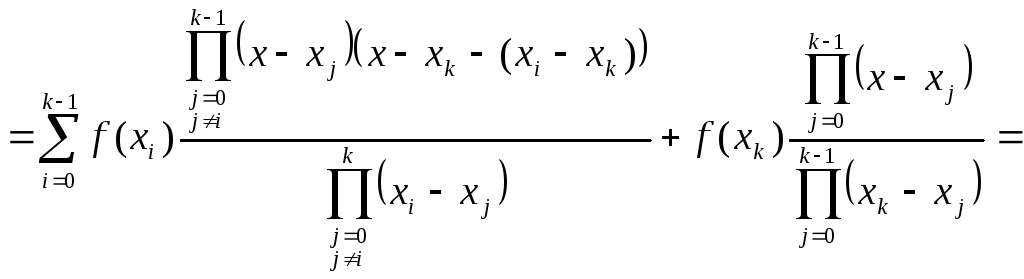
. Теорема доказана.

Замечание: если x₀ < x₁ < … < x_n , то

— интерполяционный многочлен для интерполяции вперед;

— интерполяционный многочлен для интерполяции назад.

§ 10. Интерполяция с кратными узлами

Задача: Дано: x₀, x₁, ..., x_n — узлы (различные),

m₀,..., m_n — кратности (натуральные числа),

s = m₀ +...+ m_n

Найти: многочлен g(x) степени (s–1), такой, что:

,

– – – – – – – – – –

.

Утверждение.

Многочлен g(x) определяется единственным образом.

Док-во:

Существование такого многочлена будет показано ниже, в описании алгоритма его нахождения.

Докажем единственность методом "от противного".

Предположим, существуют два многочлена степени (s–1), удовлетворяющих условиям задачи. Обозначим их разность Q(x).

Тогда Q(x) — многочлен степени (s–1) (или ниже), удовлетворяющий условиям:

,

– – – – – – – – – –

.

Следовательно, у многочлена Q(x) число x₀ – корень кратности m₀ , и т.д.

Таким образом, Q(x) имеет s корней с учетом их кратностей. Но многочлен степени (s–1) не может иметь более (s–1) корней, следовательно Q(x)0.

Утв. доказано.

Для нахождения g(x) сведем задачу к задаче поиска интерполяционного многочлена с s узлами.

Пусть  > 0 — некоторая переменная величина,

введем узлы , дляi = 0,...,n; j = 1,...,m_i.

При 0 .

При достаточно маленьком  все различны.

По таблице разделенных разностей:

…


Найдем многочлен Ньютона

Запишем в более коротком виде:

Тогда его предел при 0 имеет вид:

, где

.

Заметим, что , т.е. обычная разделенная разность, еслиi  l.

В противном случае, (доказывается по индукции).

Алгоритм нахождения g(x):

1) Записать массив предельных значений узлов , т.е. узлов

x₀,...,x₀,x₁, ...,x₁,...,x_n,..., x_n (каждый узел повторяется столько раз, какова его кратность).

2) Составить таблицу предельных значений разделенных разностей:

…


3) Составить многочлен Ньютона, используя верхнюю строку таблицы и массив узлов с повторами.

Пример. Дано: 0,1 — узлы;

2,3 — кратности;

f(0)=0, f '(0)=1,

f(1)=2, f '(1)=0, f "(1)=2.

Найти многочлен степени 4, удовлетворяющий перечисленным условиям.

1) Массив узлов с повторами: (0,0,1,1,1).

2)

0
	f '(0)=1
0		(2–1)/(1–0)=1
	(2–0)/(1–0)=2		–3
2		(0–2)/(1–0)=–2		6
	f '(1)=0		3
2		f "(1)/2=1
	f '(1)=0
2

3) g(x) = 0+1(x–0)+1(x–0)²–3x²(x–1)+6x²(x–1)² = 6x⁴–15x³+10x²+x.