- •Оглавление
- •§ 2. Существование и единственность интерполяционного многочлена
- •§ 3. Интерполяционный многочлен Лагранжа
- •§ 4. Погрешность интерполяционного многочлена Лагранжа
- •§ 5. Минимизация погрешности интерполяционного многочлена Лагранжа. Многочлен Чебышева
- •§ 6. Схема Эйткена
- •§ 7. Численное дифференцирование
- •§ 8. Погрешность простейших формул численного дифференцирования
- •§ 9. Разделенные разности. Многочлен Ньютона.
- •§ 10. Интерполяция с кратными узлами
- •§ 11. Кубическая сплайн-интерполяция
- •ГлаваIii. Численное интегрирование
- •§ 1. Простейшие квадратурные формулы. Составные формулы
- •§ 2. Метод неопределенных коэффициентов
- •§ 3. Формулы Ньютона-Котеса
- •§ 4. Формулы Гаусса
- •§ 5. Погрешность квадратурных формул. Правило Рунге.
- •ГлаваIv. Численные методы алгебры
- •§1. Системы линейных уравнений: метод простых итераций, метод Зейделя
- •§2. Метод наискорейшего спуска
- •§ 3. Обратная интерполяция для решения нелинейных уравнений
- •§ 4. Системы нелинейных уравнений: метод простых итераций
- •§ 5. Системы нелинейных уравнений: метод Ньютона
- •§ 6. Методы спуска
- •Глава V. Дифференциальные уравнения и системы
- •§ 1. Задача Коши для обыкновенных дифференциальных уравнений: применение формулы Тейлора
- •§ 2. Метод Эйлера. Методы Рунге-Кутта
- •§ 3. Конечно-разностные методы
- •§ 4. Уравнения второго порядка
Глава V. Дифференциальные уравнения и системы
§ 1. Задача Коши для обыкновенных дифференциальных уравнений: применение формулы Тейлора
Задача Коши: Дано:![]() — дифференциальное уравнение 1-го
порядка;
— дифференциальное уравнение 1-го
порядка;
![]() —отрезок, на
котором определена искомая y(x);
—отрезок, на
котором определена искомая y(x);
![]() —начальное
условие.
—начальное
условие.
Найти: функцию y(x), удовлетворяющую уравнению и начальному условию.
Пусть f(x,y) — аналитическая в окрестности т.(x0,y0) (т.е. может быть представлена рядом по степеням (x – x0) и (y – y0).
Алгоритм:
1. Известна
![]() .
.
Найдем
![]() .
.
![]() .
.
– – – – – – – – – – –
![]() .
.
2. Подставляя (x0,y0) получим:
![]() .
.
![]() .
.
![]() .
(числовые значения)
.
(числовые значения)
![]() .
.
– – – – – – – – – – –
![]() .
.
3. По формуле Тейлора составим:
![]()
Замечание: Пусть
R
— радиус сходимости ряда
![]() .
Если
.
Если![]() ,
то погрешность формулы не уменьшается
при
,
то погрешность формулы не уменьшается
при![]() .
.
Дальнейшее обобщение алгоритма:
Пусть отрезок
![]() разбит наn
частей,
разбит наn
частей,
![]() — точки деления (узлы).
— точки деления (узлы).
1. На
![]() найдем
найдем![]() .
.
Тогда
![]() .
.
2. На
![]() найдем
найдем![]() .
.
Тогда
![]() .
.
И т.д.
n.
На
![]() найдем
найдем![]() .
.
Тогда
![]() .
.
Т.е. найден набор
![]() приближенных значений искомой функции
приближенных значений искомой функции![]() в узлах
в узлах![]() .
.
§ 2. Метод Эйлера. Методы Рунге-Кутта
Пусть отрезок
![]() разбит наn
частей,
разбит наn
частей,
![]() —точки деления
(узлы),
—точки деления
(узлы),
![]() .
.
При m = 1, формула из § 1 имеет вид:
![]() —формула Эйлера.
—формула Эйлера.

Методы Рунге-Кутта — класс методов, включающий в себя метод Эйлера.
Общая идея методов:
Пусть даны параметры:
q, 2,…,q; p1,…,pq; ij, 0 < j < i q.
Найдем последовательно:
![]()
![]()
![]()
– – – – – – – – – – – – –
![]()
Тогда
![]()
Т.е.
![]() находят
последовательно по рекуррентной формуле
находят
последовательно по рекуррентной формуле
![]()
Частные случаи:
1) q = 1, p1 = 1 — метод Эйлера.
2) q
= 2, p1
=
![]() =p2;
2
= 1 = 21
=p2;
2
= 1 = 21
![]()
Обоснование справедливости формулы:
![]()
Заменим интеграл квадратурной формулой трапеций
![]()
т.к.
![]() получаем
получаем
![]()
Заменим в правой части по формуле Эйлера
![]()
Тогда
![]()
3) q
= 2, p1
= 0,
p2
= 1;
2
=
![]() =21
=21
![]()
Обоснование справедливости формулы:
![]()
Заменим интеграл квадратурной формулой прямоугольников
![]()
![]()
Заменим в правой части по формуле Эйлера
![]()
![]()
§ 3. Конечно-разностные методы
Задача: Дано:
![]()
![]()
Пусть отрезок
![]() разбит наn
частей одинаковой длины h,
разбит наn
частей одинаковой длины h,
![]() —узлы.
—узлы.
Найти:
![]() — значенияy(x)
в узлах.
— значенияy(x)
в узлах.
Явные конечно-разностные методы используют соотношения вида
![]()
где коэффициенты
![]() ,
,![]() подбираются
так, чтобы формула была точна для
многочленов наивысшей степени.
подбираются
так, чтобы формула была точна для
многочленов наивысшей степени.
Неявные конечно-разностные методы используют соотношения вида
![]()
где новое значение yk присутствует в обеих суммах.
Простейшие методы такого типа получаются на основе квадратурных формул интегрирования:
![]()
![]()
По формуле трапеций получаем
![]()
![]()
— неявный конечно-разностный метод.
Для использования формулы Симпсона применяют другое равенство
![]()
![]()
![]()
— неявный конечно-разностный метод.
Формулу прямоугольников
применим также для равенства
![]()
![]()
![]()
—явный конечно-разностный метод.
Замечание: вторая и третья формулы имеют низкую сходимость, т.е. при уменьшении h погрешность уменьшается медленнее, чем в первой формуле.
§ 4. Уравнения второго порядка
I.
Дифференциальное уравнение, в котором
отсутствует![]() .
.
Задача Коши: Дано:
![]()
![]() ,
,
![]() – начальные условия
– начальные условия
Пусть отрезок
![]() разбит наn
частей одинаковой длины h,
разбит наn
частей одинаковой длины h,
![]() —узлы.
—узлы.
Найти:
![]() — значенияy(x)
в узлах.
— значенияy(x)
в узлах.
Для каждого узла выполняется
![]()
Заменим в левой части вторую производную формулой численного дифференцирования по трем точкам:
![]()
Правую часть заменим линейной комбинацией
![]()
Тогда получим
формулу
![]()
явный метод.
Если правую часть
заменим другой линейной комбинацией
![]() ,
то получим формулу
,
то получим формулу![]()
неявный метод.
Коэффициенты
![]() подбираются
так, чтобы формула была точна для
многочленов наивысшей степени.
подбираются
так, чтобы формула была точна для
многочленов наивысшей степени.
Пример. Метод Нумерова — неявный метод, m = 1, четвертого порядка точности.

Вывод формулы методом неопределенных коэффициентов:
Нужно найти формулу
![]()
точную для y(x), являющейся многочленом до четвертой степени.
Пусть xk = 0.
Для y(x) = x2
![]()
Для y(x) = x3
![]()
Для y(x) = x4
![]()
Получается система

Решение системы:
![]()
Применение метода:
1) По формуле Эйлера
находим
![]() .
.
2) По рекуррентной формуле находим
![]() .
.
II. Задача Коши: Дано:
![]()
![]() ,
,
![]() – начальные условия
– начальные условия
отрезок
![]() разбит наn
частей одинаковой длины h,
разбит наn
частей одинаковой длины h,
![]() —узлы.
—узлы.
Найти:
![]() — значенияy(x)
в узлах.
— значенияy(x)
в узлах.
В ходе решения
будут найдены также
![]()
значения
![]() в узлах.
в узлах.
Явный метод использует равенства
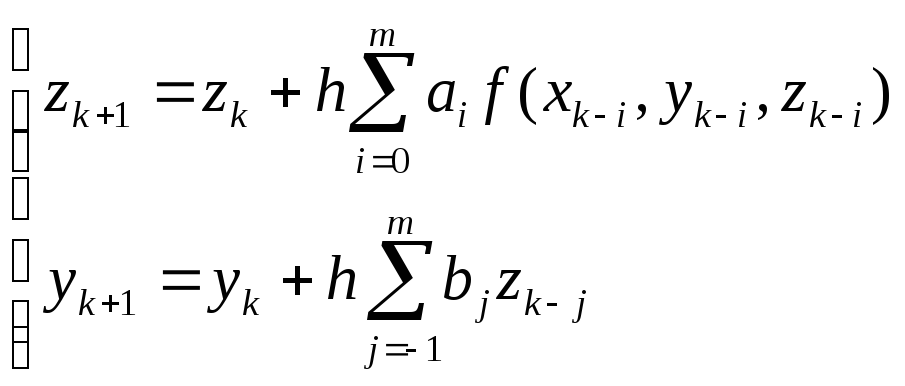
Неявный метод использует равенства

Пример. Явный метод, m = 0.