§ 11. Кубическая сплайн-интерполяция
Пусть [a,b]
разбит на N
равных частей. Точки деления a
= x0,
x1,
..., xn
= b.
Длина каждого участка
.
Опр. Сплайн — функция, непрерывная вместе с производными до некоторого порядка на [a,b], являющаяся многочленом на каждом [xi–1,xi]
("кусочная функция").
Степень сплайна — максимальная из степеней многочленов.
Дефект сплайна — разность между степенью сплайна и наивысшим порядком непрерывной производной.
Сплайн-интерполяция — замена функции f(x) на сплайн, имеющий в узлах те же значения, что и f(x), и те же значения производных.
Опр. Кубический сплайн — сплайн третьей степени, имеющий непрерывную производную первого порядка.
Обозначение: S3(x).
Опр. Наклон сплайна
в точке xi
— значение производной
.
Рассмотрим один отрезок [xi–1,xi], h = xi – xi–1.
Пусть fi–1, fi — значения функции (следовательно, сплайна тоже),
fsi–1,fsi — значения производной функции.
Как в задаче интерполяции с кратными узлами, кратность каждого узла равна 2. Тогда существует многочлен степени 2+2–1 = 3, удовлетворяющий условиям задачи.
Составим таблицу предельных значений разделенных разностей:
|
xi–1 |
fi–1 |
|
|
|
|
|
|
fsi–1 |
|
|
|
xi–1 |
fi–1 |
|
|
|
|
|
|
|
|
|
|
xi |
fi |
|
|
|
|
|
|
fsi |
|
|
|
xi |
fi |
|
|
|
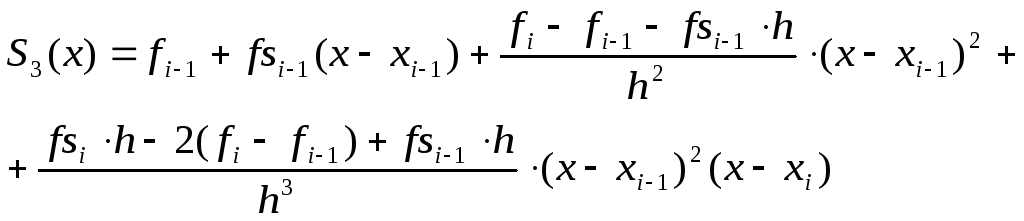
После преобразования, найденную функцию можно записать в виде линейной комбинации значений fi–1, fi и fsi–1,fsi:
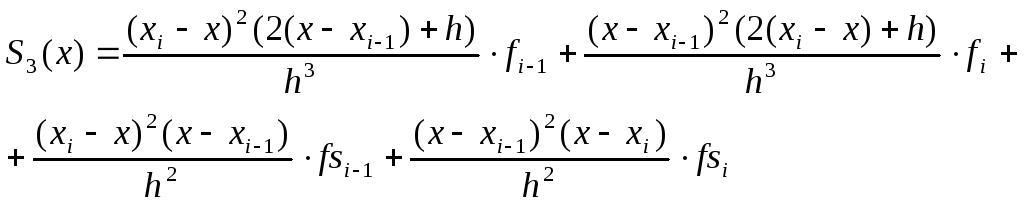
Применение кубической сплайн-интерполяции:
При большом количестве N узлов интерполяции, когда поиск интерполяционного многочлена большой степени требует большого объема вычислений, вместо него находят кубический сплайн, составленный из многочленов третьей степени, определенных каждый на своем отрезке между узлами.
Если не известны наклоны сплайна (т.е. значения производной в узлах), вычисляют их примерное значение по формулам численного дифференцирования:
,
для i
= 1,...,N–1
,
.
ГлаваIii. Численное интегрирование
§ 1. Простейшие квадратурные формулы. Составные формулы
Задача: вычислить
дляf(x),
непрерывной на [a,b].
Опр. Квадратурная
формула —
,
определяемая узлами
x0, x1, ..., xn и весами q0, ..., qn .
Квадратурная формула называется точной для многочленов степени m, если для любого многочлена, степени ≤ m, подставленной вместо f(x), формула дает точное равенство.
I. Формула прямоугольников.
.
Формула точна для многочленов степени 1.
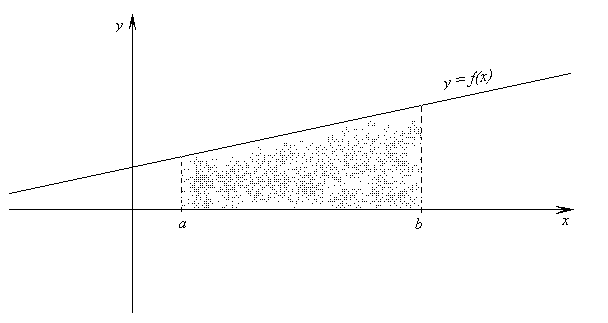
II. Формула трапеций.
,
где
.
Формула также точна для многочленов степени 1.
III. Формула Симпсона.
Пусть
.
Формула также точна для многочленов степени 2 (без док-ва).
Составные формулы получаются, если [a,b] разбить на N частей, на каждой части применить простую формулу, и результаты сложить.
Пусть
Составная формула прямоугольников:
.
Составная формула трапеций:
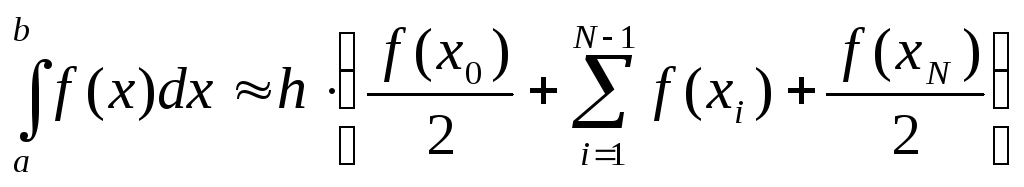
Пусть
Составная формула Симпсона:
.
§ 2. Метод неопределенных коэффициентов
Пусть известны узлы x0, ..., xn на [a,b].
Найдем квадратурную
формулу
,
точную для любых многочленов степениm.
Тогда при подстановке простых многочленов
1=x0, x, x2,...,xm получится система уравнений:
,
для j
= 0,...,m.
Это СЛУ с неизвестными q0, ..., qn.
,
для j
= 0,...,m.
В этой СЛУ (m+1) уравнений, (n+1) неизвестных.
Если m = n, то главный определитель системы
— определитель Вандермонда (транспонированный).
Следовательно, решение q0, ..., qn существует и единственно.
Пример.
Пусть m
=2,
n =2,
СЛУ:
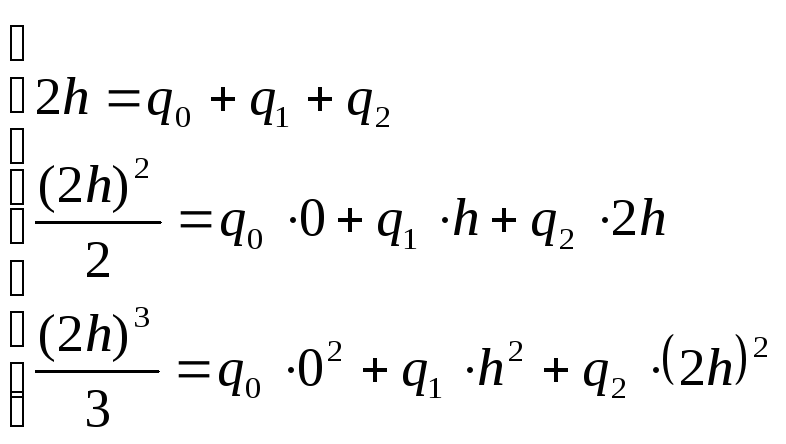
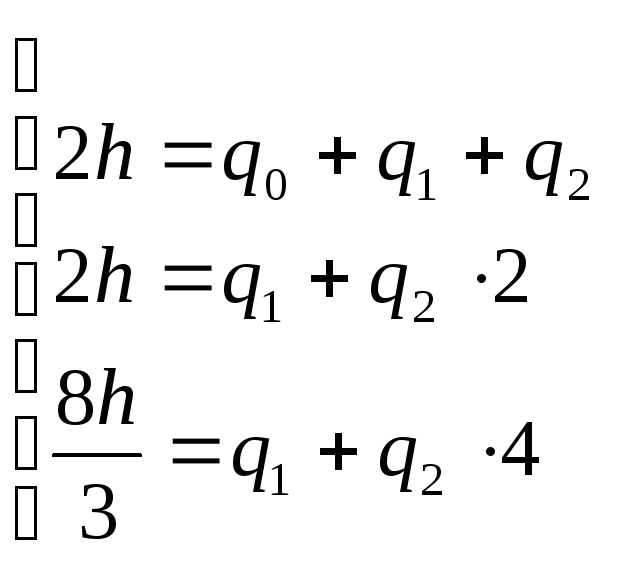
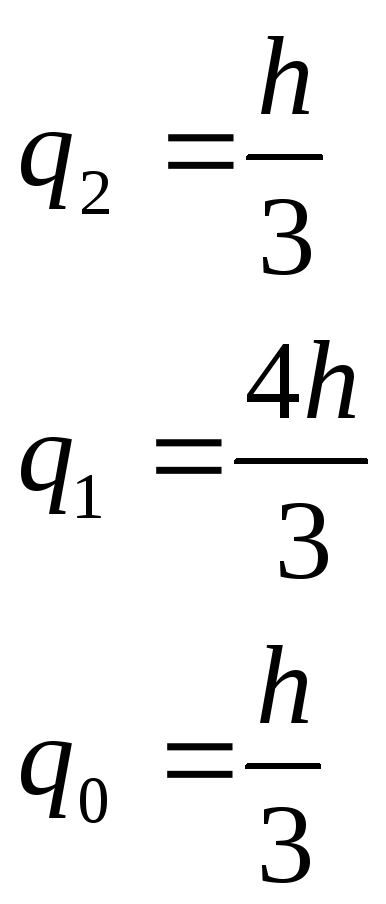
Получили формулу Симпсона.