§ 5. Погрешность квадратурных формул. Правило Рунге.

Пусть квадратурная формула точна для многочленов степениm (n ≤ m). Для оценки погрешности воспользуемся разложением f(x) по формуле Тейлора:

.

Тогда

.

Т.е. — погрешность квадратурной формулы.

Пример.

1) Для простейших формул прямоугольников и трапеций

.

2) Для формулы Симпсона

.

Теперь воспользуемся разложением f(x) по формуле Тейлора степени (m+1):

/

Тогда

.

Опр. Главным членом погрешности называется .

Правило Рунге — способ оценки главного члена погрешности без использования производной (m + 1) порядка.

Пусть I_h — приближенное значение интеграла , вычисленное по составной квадратурной формуле с длиной участка.

Тогда .

.

ГлаваIv. Численные методы алгебры

§1. Системы линейных уравнений: метод простых итераций, метод Зейделя

Задача: Дано: ,i=1,...,m.

Найти: , удовлетворяющее системе.

Пусть система Крамеровская, т.е. m = n.

Запишем систему в матричной форме:

(1),

где – столбец неизвестных,– столбец свободных коэффициентов.

Метод простых итераций:

1. Преобразуем уравнение (1) в уравнение вида (2) (B=E-A);

2. Составим рекуррентную формулу: (3);

3. Выберем любое начальное приближение .

По формуле (3) найдем ,, …,;

4. Если метод сходится, то последнее найденное приближение приблизительно равно решению системы (2).

Определения нормы вектора:

Опр. 1. .

Опр. 2. .

Опр. 3. .

Определения нормы матрицы, согласованной с нормой вектора:

Опр. .

Следовательно:

Опр. 1. .

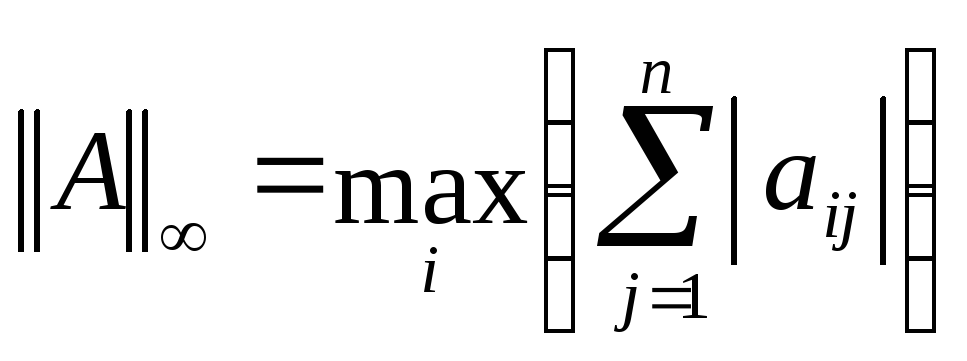Опр. 2. .

Опр. 3. , где– собственное значение матрицы,– сопряженная кA матрица (.

Замечание: Если уменьшается при , то метод простых итераций сходится.

Теорема. (Достаточное условие сходимости метода простых итераций)

Если ||B|| < 1, то система (2) имеет единственное решение, и итерационный процесс по формуле (3) сходится со скоростью убывающей геометрическое прогрессии.

Док-во:

1. Если – решение системы (2), то

.

Тогда однородная система имеет решение, удовлетворяющее

, т.е. решение существует (нулевой вектор) и единственное.

Следовательно система (2) имеет единственное решение (по теореме об общем решении СЛУ, равной сумме общего решения однородной системы и частного решения неоднородной).

2. Пусть – точное решение системы (2).

Тогда – погрешность на шагеk, и

; при.

Если обозначить , то норма погрешности меньше членов убывающей геометрической прогрессии с шагомq.

Теорема 2. (без док-ва) (Необходимое и достаточное условие сходимости метода простых итераций)

Пусть система (2) имеет единственное решение. Итерационный процесс по формуле (3) сходится к решению системы (2) при любом начальном приближении тогда и только тогда, когда все собственные значения матрицы B по модулю меньше 1.

Своеобразная модификация метода простых итераций – метод Зейделя.

Метод Зейделя:

Пусть в системе (1) в матрицеA все диагональные элементы отличны от нуля.

1. Определим матрицы ;.

Получим систему (4).

2. Построим рекуррентную формулу (5).

3. Выберем любое начальное приближение .

Система (5) имеет вид

Из первого уравнения системы (5) найдем , из второго уравнения системы (5) найдем, и т.д. Таким образом, найдем. Аналогично, найдем, …,.

4. Если норма разности уменьшается, то метод сходится, и последнее найденное приближениеприблизительно равно решению системы (4).

Замечание: Формула (5) равносильна формуле . Тогда. Итерационный процесс сходится, если все собственные значения матрицыпо модулю меньше 1.

Теорема 3. (без док-ва)

Если A – вещественная, симметричная, положительно определенная (т.е. все главные миноры положительны) матрица, то метод Зейделя сходится.