Matan__teoria

2). Для вычисления интеграла ∫ a d r по плоской линии BC с
	BC
уравнением y = y(x), x [b,c] следует:
а) записать интеграл в координатной форме ∫ P(x, y)dx + Q(x, y)dy ,
	BC
б) заменить y	в функциях P, Q на y(x),
в) заменить dy	′
	на y (x)dx,
г) вычислить получившийся определенный интеграл по отрезку [b, c].

3). В случае центрального поля a = f (r) r следует учесть, что r 2 = r 2 ;

дифференцируя это равенство, получим 2r d r = 2r d r									и
							rC
	∫ a d r = ∫ f (r) r d r = ∫ f (r) r d r ,
	BC	BC					rB
т.е. линейный интеграл поля сведен к определенному интегралу.
						= {x2, − yz, z}
Пример 11.1. Вычислить работу силы F									по прямолинейному пере(
мещению из точки B(1, 2, −1) в точку C (3, 3, 2) .
Решение. Работа A силы F вычисляется по формуле
	A= ∫			= ∫ x2dx− yz dy +z dz .
		F d r
	BC				BC
Для вычисления этого интеграла составим уравнение прямой BC :
		x −1	=		y − 2	=	z +1	= t .
		3 −1			3− 2
						2 +1
Отсюда x = 2t +1, y = t + 2, z = 3t −1;				dx = 2dt, dy = dt, dz = 3dt .

Найдем значение параметра t , соответствующее точке B . Для этого подставим

	абсциссу x = 1 точки B в формулу x = 2t +1. Получим				tB = 0 . Аналогично найдем
	tC =1 . Заменяя в интеграле x, y,		z, dx, dy, dz их выражениями, получим
	A = ∫	1		2
		2
		x dx − yz dz + z dz = ∫	(2t +1) 2 − (t + 2)(3t −		1) + (3t −1) 3 dt = 26 3.
	BC	0

Пример 11.2. Найти циркуляцию поля a = yi + 2 x j вдоль линии

─ дуга параболы y 2 = x, OAB ─ ломаная (рис. 67).										y
Решение. Циркуляцию поля a вычислим по формуле
C(a) = a d r		∫	a d r		+	∫	a d r +	∫	a d r .
∫
OABO	[OA]				[AB]		BO
На отрезке OA имеем y = 0, dy = 0. Поэтому
I1 = ∫	a d r =			∫	ydx + 2 xdy = 0 .
[OA]				[OA]						0
На отрезке AB имеем x =1,				dx = 0,			0 ≤ y ≤1. Поэтому
									1
				I2 =	∫ ydx + 2 xdy = ∫2dy = 2 .
					[AB]				0

OABO , где OB

B(1,1)

Ax

Рис. 67

91

На дуге BO имеем x = y2,

y = y

(y − параметр),

dx = 2y dy,

y

B

=1,

y = 0 . Поэтому

O

I3 = ∫ y dx + 2xdy = ∫0 (y 2y + 2y

2)dy = ∫0 4y2dy = −4 .

BO

1

1

3

Окончательно, C(a) = I + I

2

+ I

3

= 0+ 2 − 4 = 2 .

1

3

3

y

x

Пример 11.3. Вычислить циркуляцию поля a

=

−

,

по окружности (L)

x2

+ y2

x2

+ y2

радиусом R с центром в начале координат, ориентированной против часовой стрелки.

Решение. Циркуляция поля a вычисляется по формуле

	C(a) =		a d r =		−	y	dx+	x	dy .
						x2 + y2		x2 + y2
		∫		∫
		(L)		(L)

Для вычисления этого интеграла запишем параметриче(

ские уравнения окружности (L): x = Rcost,	y = Rsint .
Тогда dx = −Rsint dt , dy = Rcost dt ; угол t	при движении

против часовой стрелки меняется от 0 до 2π (рис. 68). По(

	2π −Rsint (−Rsint)+ Rcost Rcost										2π
этому C(a) =	∫	R	2	cos	2	t + R	2	sin	2	t	dt = ∫ dt = 2π .
	0										0

y

(L)

t

x

РисРис. .6868

11.4. Формулы Грина и Стокса. Ротор поля

Циркуляцию, как линейный интеграл поля по замкнутому контуру, можно вы( числять способами, изложенными в п. 11.3. Однако часто удобно вычислять цир( куляцию плоского поля по формуле Грина, а циркуляцию пространственного поля ─ по формуле Стокса.

Если при обходе замкнутого контура ограниченная область остается слева, то направление обхода называют положительным. Обход в противопо( ложном направлении называют отрицательным.

Теорема 11.1. Пусть функции P(x, y), Q(x, y) и их частные производные непрерывны в области (D) с положительно ориентированной границей (L). То( гда имеет место следующая формула Грина:

	∫			∫∫
		P dx+Qdy =			∂Q −∂P dxdy		.	(11.5)
					(D) ∂x	∂y
	(L)
Доказательство проведем для			области		(D),	описываемой		неравенствами

ϕ1(x) ≤ y ≤ ϕ2(x), a ≤ x ≤ b (рис. 69). Сначала проверим равенство

∫		∫∫	∂y	(11.6)
	Pdx=−		∂P dxdy .
(L)		(D)	∫
Сведем криволинейный интеграл P(x, y)dx				к опреде(
			L
ленному интегралу, подставляя			y = ϕ1(x) на линии AKB
и y = ϕ 2(x) на линии BMA:

y	y = ϕ2	(x)
	M	B

A

Ky = ϕ1(x)

0	a	b	x

O

Рис. 69

92

P(x, y), Q(x, y)

∫		∫		∫		b		a
	P(x, y)dx =		P(x, y)dx +		P(x, y)dx =	∫	P(x, ϕ1(x))dx+	∫
									P(x, ϕ2	(x))dx,
(L)		AKB		BMA		a		b

b

∫ P(x, y)dx = ∫[P(x, ϕ1(x))−P(x, ϕ2(x))]dx.

(L) a

Теперь преобразуем двойной интеграл, сведя его сначала к повторному, а затем к определенному интегралу:

	b	ϕ2(x)	b		y = ϕ2	(x)	b
− ∫∫	∂P dxdy = −∫dx	∫	∂P dy = −∫dx[P(x, y)]				= ∫ P(x,ϕ1(x))− P(x,ϕ2	(x)) dx .
					y = ϕ1	(x)
(D)	∂y	ϕ1(x)	∂y
	a		a				a

И криволинейный, и двойной интегралы из формулы (11.6) равны одному и то( му же определенному интегралу и, следовательно, равны между собой. Анало( гично проверяется равенство

∫		∫∫ ∂x
	Qdy =		∂Q	dxdy .	(11.7)
(L)		(D)

Складывая равенства (11.6) и (11.7), получим формулу Грина.

Замечание. Нарушение условий теоремы Грина может привести к неверным

результатам. Например, для поля a = −

y

,

x

нетрудно проверить, что

+ y2

+ y2

x2

x2

∂Q

∂P

∂

x

∂

−y

1 (x2 + y2)− x 2x 1 (x2 + y2)− y 2y

−

=

−

=

+

= 0 ,

2

2

2

2

(x2 + y2)

2

(x2

+ y2)

2

∂x

∂y

∂x x

+ y

∂y x

+ y

но циркуляция поля по окружности (L)

с центром в начале координат отлич(

наот нуля, C (a, L) = 2π

(пример 11.3). В этом примере нарушены условия тео(

ремы Грина, т.к. внутри контура (L) содержится точка (0, 0), в которой функции не определены.

Пример 11.4. Используя формулу Грина, вычислить циркуляцию поля a = yi + 2 x j вдоль линии OABO (рис. 67).

Решение. Вычислим циркуляцию C =				∫	ydx+2 xdy		, используя формулу Грина
				OABO
		∂Q			1	1	1
для P = y, Q = 2x :	C = ∫∫						dx = ∫(1− y	2	)dy = 1	− 1	= 2 .
			− ∂P dxdy = ∫∫ dxdy = ∫dy ∫
	(D)	∂x	∂y	(D)	0	y2	0			3	3

Сравните это решение с решением примера 11.2, где циркуляция этого поля была вычислена без формулы Грина.

Для обобщения формулы Грина на пространственный случай введем по( нятие ротора векторного поля a .

Ротором векторного поля a = {P, Q, R} называется вектор

i

j

k

∂

∂

∂

rot a

=

= × a

.

(11.8)

∂x

∂y

∂z

P

Q

R

93

При вычислении rot a

следует разложить определитель по элементам первой

строки. Учитывая, что

∂

P =

∂P

,

∂

Q =

∂Q

,

∂

R =

∂R

и т. д., получим

∂x

∂x

∂x

∂x

∂y

∂y

=

∂R

−

∂Q

− (∂R −

∂P )

∂Q

rot a

i

j

+

∂x

− ∂P k .

∂y

∂z

∂x

∂z

∂y

Понятие ротора позволяет удобно вычислять циркуляцию векторного поля, опираясь на следующую теорему (доказательство теоремы опустим).

Теорема 11.2. Пусть функции P(x, y, z), Q(x, y, z), R(x, y, z) и их частные производные непрерывны на ориентированной поверхности (σ ), натянутой на контур (L), причем ориентации контура (L) и поверхности (σ ) согласованы. Тогда имеет место следующая формула Стокса:

a d r =

∫

rot a dσ

.

(11.9)

∫

(L)

(σ)

В этой формуле ориентации контура (L)

и поверхности (σ )

n

согласованы, т. е., глядя с конца выбранных нормальных векто(

n

ров поверхности (σ ), обход контура (L)

виден против часовой

(σ)

стрелки (рис. 70).

Итак, по формуле Стокса циркуляция поля a

по контуру

(L)

(L) равна потоку ротора поля a

через поверхность (σ ), натя(

нутую на контур (L).

Рис. 70

a = (20x4

Пример 11.5. Для поля

+1)z i − 5y

j

+ 4x5 k

найти его

циркуляцию по окружности

x2 + z2 = 9 , лежащей в плоскости

z

n

y = 4 и ориентированной против часовой стрелки, если смотреть

с конца оси OY (рис. 71).

i

Решение.

Циркуляция

поля

a

вычисляется

по

формуле

0

y

x

4

∫

C = a d r . Непосредственное вычисление этого интеграла до(

статочно трудоемко. Посмотрим, облегчит ли вычисление цирку(

Рис. 71

ляции применение формулы Стокса. Для этого вычислим ротор

i

j

k

∂

∂

∂

rot a =

= i

(0 −

0)

− j

(20x4 −

20x4 −1)+ k

(0

− 0) =

j.

∂x

∂y

∂z

(20x4 +1) z −5y

4x5

∫

∫

∫

rot a d

σ =

(rot a,n)dσ.

По формуле Стокса имеем: C = a d r =

(L)

(σ)

(σ)

В качестве поверхности (σ ), натянутой на окружность, возьмем круг, ограни(

ченный этой окружностью. Нормальный вектор к этой поверхности направлен

вдоль оси

2

=1

;

OY , т.е. n

= j ; скалярное произведение rot a

n =

j

j =

j

C = ∫∫(rot a,n)dσ = ∫∫ dσ = S = π R2 = 9π .

(σ )

(σ )

94

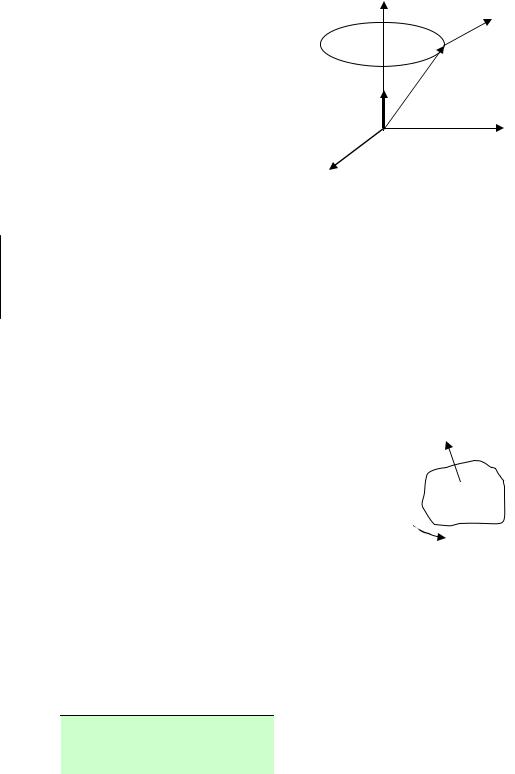
Остановимся более подробно на свойствах ротора.

Физический смысл ротора

Пусть твердое тело вращается с постоянной угловой скоростью ω . Найдем по( ле линейных скоростей точек тела и ротор этого поля.

Рассмотрим систему координат, направив ось Oz по оси вращения (рис. 72).

	Как известно из кинематики, линейная скорость v точки									z
	M равна векторному произведению v = ω × r , где r ─ ра(
	диус(вектор точки M , r = {x, y, z} , ω							─ вектор угловой
	скорости, направленный по оси вращения с длиной, рав(									M
	ной величине угловой скорости ω , т. е.							ω = ω k = {0, 0, ω} .		ω
	Найдем поле линейных скоростей:
	v = ω × r =		i	j	k					0
			0 0 ω
							= −ω y i		+ω x j .
			x	y	z				x	Рис. 72

v

y

Ротор этого поля вычислим по формуле (11.8):

			i			j		k
	=		∂			∂		∂
rot v
			∂x			∂y		∂z
		−ω y			ωx			0

		∂		∂
	= i		0 −		(ωx)
		∂y		∂z

∂

∂

∂

∂

− j

(

0 −

(−ω y))+ k

(ω x) −

(−ω y)

= 2ωk

= 2ω.

∂x

∂z

∂x

∂y

Таким образом, ротор поля линейных скоростей в любой точке равен удвоен( ному вектору угловой скорости.

В произвольном поле его ротор, вычисленный в точке M , также характе% ризует вращательную способность поля в этой точке.

Инвариантное определение ротора

Рассмотрим некоторую поверхность (σ ), содержащую точку M ,

и единичный нормальный вектор n этой поверхности (рис. 73). Вычислим по формуле Стокса циркуляцию поля a по произвольному контуру (L), лежащему на поверхности (σ ):

			∫		∫
C (a , L) = ∫	a d r	=		rot a dσ =		(rot a,n)dσ .
(L)			(σ)		(σ)

n

•M

(σ)

(L)

Рис. 73

Воспользуемся теоремой о среднем для поверхностного интеграла 1(го рода:

C (a, L) =	∫	(rot a,n)dσ = (rot a,n) σ = (прn rot a) σ
		M	M

(σ)

(прn rot a) =	C (a , L)	.
M	σ

Переходя в последнем равенстве к пределу при стягивании поверхности (σ ) в

точку M , получим:

(прn rot a)		=	lim	C (a, L)		.	(11.10)
				σ
	M		(σ ) → M
			(σ ) n

Эту величину называют плотностью циркуляции поля a в точке M в направле( нии вектора n . Плотность циркуляции, как проекция прn rot a , принимает

95

наибольшее значение, равное rot a , когда векторы rot a и n сонаправлены. По(

этому получаем следующее инвариантное ( не зависящее от системы коорди( нат) определение ротора.

Ротор поля a в точке M есть вектор, удовлетворяющий условиям:

а) в направлении этого вектора плотность циркуляции поля a в точке M принимает наибольшее значение,

б) по величине он равен наибольшей плотности циркуляции поля a в точке M.

Дифференциальные свойства ротора

1)	rot c = 0,			= 0,		− постоянный вектор),
		или × c			( c
2)	rot r = 0,			= 0,		− радиус(вектор),
		или × r			( r
3)	rot(a + b)= rot a + rotb , или × (a						+ b)= × a + × b ,
	rot( f a)								a) = f
4)		= f rot a + (grad f )× a , или × ( f								( × a)+( f )×a,
( f	− скалярное поле, a − векторное поле),
5)									( c− константа),
	rot(c a)	= c rota,	или × (c a) = c ×a,
	rot( f c)								)×c , (c − постоянный вектор),
6)		=(grad f )× c , или ×( f					c) =( f
					( f (r) r )= 0 .
7)	rot( f (r) r )= 0 или ×

Проверим эти свойства:

свойства 1) ─ 3) проверяются непосредственным вычислением,

i

j

k

i

j

k

i

j

k

4) rot( f a) =

∂

∂

∂

= f

∂

∂

∂

+

∂f

∂f

∂f

= f rot a + (grad f )× a ,

∂x

∂y

∂z

∂x

∂y

∂z

∂x ∂y ∂z

f P f Q f R

P Q R

P Q R

свойство 5) есть следствие свойства 4) при f = c , свойство 6) есть следствие свойства 4) при a = c ,

7) по свойству 4) ротора rot f (r) r = f (r) rot r + (grad f (r))× r , а по свойствам гра(

	диента grad f (r) = f ′(r) grad r = f	′(r)	r	. Учитывая, что rot r = 0, r × r = 0, получим
			r
						r
	rot f (r) r	= f (r) rot r			+ f ′(r)			× r	= 0 .
						r

11.5.Условия независимости линейного интеграла от формы пути

Вразличных приложениях важно знать, зависит ли линейный интеграл поля

∫a d r от формы кривой интегрирования или он зависит только от начальной и

конечной точек этой кривой (с физической точки зрения – зависит ли работа си( лы от формы пути). Рассмотрим три условия независимости линейного интегра(

ла поля от формы пути интегрирования. Как и раньше, будем предполагать, что вектор(функция a(M ) = {P(M ), Q(M ), R(M )} дифференцируема.

96

Теорема 11.3 (о равенстве нулю циркуляции). Для того чтобы линейный ин( теграл поля не зависел от формы пути интегрирования, необходимо и доста( точно, чтобы циркуляция поля по любой замкнутой кривой равнялась нулю.

Доказательство. Вычислим циркуляцию поля a							по произвольной замкнутой
кривой ABCDA (рис. 74)
C (a) = a d r	=	∫	a d r	+	∫	a d r =	∫	a d r −	∫	a d r.
∫
ABCDA		ABC			CDA		ABC		ADC
Из этого равенства следует: циркуляция C(a) равна нулю тогда
и только тогда, когда ∫	a d r =		∫	a d r , т. е. интеграл ∫ a d r						D	C
ABC			ADC

по двум произвольным линиям с общим началом и общим кон( цом принимает одно и то же значение и, значит, не зависит от формы пути интегрирования.

Теорема 11.3 дает критерий независимости линейного инте( грала поля от формы пути интегрирования, однако этот крите( рий трудно проверить.

B

A

Рис..74

Для формулировки следующего более эффективного критерия введем новое понятие. Область назовем односвязной, если на любой ее замкнутый контур можно натянуть поверхность, целиком лежащую в этой области.

Например, односвязными областями будут круг, шар, куб; к неодносвязным областям относятся кольцо, тор (“бублик”) (рис. 75).

zy

0	y
	x
x	Рис.75

Теорема 11.4 (о равенстве нулю ротора). Для того чтобы линейный инте( грал поля не зависел от формы пути интегрирования, необходимо, а для одно( связного поля и достаточно, чтобы ротор поля в каждой точке равнялся нулю.

Необходимость. Пусть линейный интеграл поля a не зависит от формы пути интегрирования и, значит, циркуляция C (a , L) по любому замкнутому контуру равна нулю. Тогда по формуле (11.10)

	(прn rot a)		=	lim	C (a , L)	= 0 ,
		M			σ
				(σ ) → M
				(σ ) n

т.е. проекция ротора на любой вектор n в любой точке M равна нулю. Поэтому rot a = 0 в любой точке поля.

97

Достаточность. Пусть rot a = 0 в односвязной области (D). Возьмем любой замкнутый контур (L) в (D). В силу односвязности области (D) на контур (L) можно натянуть поверхность (σ ), целиком лежащую в области (D). Вычислим циркуляцию поля a по контуру (L), используя формулу Стокса и условие rot a = 0 :

C (a, L) =

a d r = (rot a,n)dσ =0 .

∫

∫

(L)

(σ)

Так как циркуляция поля a по любому замкнутому контуру (L)

равна нулю, то

по теореме 11.3 интеграл

∫a d r не зависит от формы пути. Теорема доказана.

(L)

Теорема 11.5 (о подынтегральном выражении). Для того чтобы ли(

нейный интеграл поля

∫a d r

не зависел от формы пути интегрирования,

(L)

необходимо и достаточно, чтобы подынтегральное выражение a d r бы(

ло полным дифференциалом некоторой функции U .

Необходимость. Пусть

∫a d r не зависит от формы пути. Покажем, что функция

(L)

U (M ) = ∫ a d r

есть искомая функция (M0 ─ фиксированная точка), т.е. a d r = dU .

(M0M)

Для этого вычислим частное приращение

xU = U (x + x, y, z) −U (x, y, z) = U (M1)−U (M ) = ∫ a d r − ∫ a d r.

z

(M0 M 1)

(M0 M)

M M1

M0

Так как интеграл ∫a d r не зависит от формы пути, то кривую

y

(L)

M0 M выберем произвольно, а в качестве кривой M0 M1

возьмем

0 x x + x x

кривую M0 M и отрезок прямой MM1

(рис. 76). Тогда по свойству

Рис. 76

аддитивности интеграла

a d r −

a d r +

a d r

a d r.

x

U =

∫

∫

a d r =

∫

∫

a d r −

∫

=

∫

(M0 M 1)

(M0 M)

(M0 M)

(M M 1)

(M0 M)

(M M 1)

Запишем интеграл в координатной форме и учтем, что на отрезке MM1

меняется

только x , а y, z − постоянны, значит, dy = 0,

dz = 0 и

x+ x

xU = ∫ a d r = ∫ Pdx + Q dy + Rdz = ∫ P(x, y, z)dx.

(M M 1)

(M M1)

x

К получившемуся определенному интегралу применим теорему о среднем:

x+ x	P(x, y, z)dx = P(x, y, z) x ;
xU = ∫
	ɶ

x

	здесь x− некоторая промежуточная точка между x и x + x . Тогда
	ɶ		xU		P(x, y, z) x
	′					ɶ
	Ux =	lim		= lim	ɶ	= lim P(x, y, z) = P(x, y, z).
			x		x
		x→0		x→0		x→0

98

Итак, U′x = P(x, y, z) . Аналогично можно показать, что U′y = Q(x, y, z), U′z = R(x, y, z). Тогда a d r = Pdx + Qdy + Rdz =U′x dx +U′y dy +U′z dz = dU .

Достаточность. Пусть существует функция U(x, y, z) такая, что a d r = dU . Рассмотрим произвольную дугу AB с параметрическими уравнениями

	x = x(t), y = y(t), z = z(t); t [tA; tB ].
Сведем интеграл	∫ a d r	по этой дуге к определенному интегралу и применим
	AB
формулу Ньютона(Лейбница
		t
∫ a d r	= ∫ dU(x, y, z) = ∫B dU (x(t), y(t), z(t)) = U (x(t), y (t), z (t))			ttBA=
AB	AB	tA
	= U (xB , yB , zB) −U (xA , yA , zA) = U(B) −U(A).

Таким образом, значение интеграла ∫ a d r зависит только от точек A, B и не

AB

зависит от формы линии AB .

Попутно мы получили важную формулу, являющуюся аналогом формулы

Ньютона(Лейбница для криволинейных интегралов:
	∫ dU = U (B) −U (A).		(11.11)
	AB
Теоремы 11.3, 11.4, 11.5 иногда объединяют в одну:

Если область (D) является односвязной, то четыре условия равносильны: 1) линейный интеграл ∫a d r не зависит от формы пути интегрирования;

(L)

2)линейный интеграл ∫a d r по любому замкнутому контуру в (D) равен нулю;

(L)

3)rot a = 0 во всех точках области (D);

4)выражение a d r является полным дифференциалом некоторой функции U .

12.Некоторые классы векторных полей

12.1. Потенциальное поле

Как и раньше, предполагаем, что координаты вектора поля a ─ функции P , Q, R непрерывны и имеют частные производные.

Векторное поле a называется потенциальным, если оно является полем градиента некоторой скалярной функции U , т.е. a = gradU ; при этом функцию U называют скалярным потенциалом векторного поля.

Напомним, что gradU = U′x i +U′y j +U′z k . Так как grad(U +C) = gradU , то U + C также является потенциалом.

99

Свойства потенциального поля

1). Поле a является потенциальным с потенциалом U тогда и только тогда, когда a d r = dU .

2). Односвязное поле a потенциально тогда и только тогда, когда в каждой точке поля rot a = 0 .

3). В потенциальном поле линейный интеграл ∫a d r не зависит от формы пути.

(L)

4). В потенциальном поле циркуляция по любому контуру, не охватываю( щему особых точек поля, равна нулю.

5). В потенциальном поле циркуляции по контурам, охватывающим все особые точки поля, равны между собой.

6). В потенциальном поле линейный интеграл по дуге равен разности по( тенциалов конца и начала дуги.

Проверим эти свойства.

1). Поле a ─ потенциально, т.е. a = gradU = {U′x, U′y , U′z} тогда и только тогда, когда a d r = {U′x, U′y, U′z} {dx, dy, dz} = U′x dx +U′y dy +U′z dz = dU .

2). Это свойство следует из свойства 1) и теорем 11.5, 11.4. 3). Это свойство следует из свойства 1) и теоремы 11.5.

4). Это свойство является следствием свойства 2) и теоремы 11.4, так как поле внутри контура, не охватывающего особых точек, является односвязным.

5). Пусть (L), (l ) ─ контуры, окружающие все особые точки P1,..., Pn поля (рис. 77); ориентируем контуры так, чтобы при обходе ограниченная ими область (σ )

оставалась слева, т.е. (L)− против часовой стрелки, (l)− по часовой стрелке; контуры с такой ориентацией обозначим соответственно (L+ ), (l − ). На поверх(

ности (σ )

с границей (γ ) = (L+) (l −)

поле потенциально, и потому rot a = 0 по

свойству 3) и теореме 11.4. Тогда по формуле Стокса

=

∫

=0 .

(L+ )

a d r

rot a dσ

∫

(σ)

(γ)

(σ)

(l −)

С другой стороны,

•P1

=

+

=

−

•Pn

a d r

a d r

a d r

a d r

a d r

,

∫

∫

∫

∫

∫

(γ)

(L

+

)

−

)

(L

+

)

(l

+

)

(l

и, следовательно,

∫

a d r =

∫

a d r .

Рис. 77

(L + )

(l + )

6). Если поле a потенциально и U ─ его потенциал, то a d r = dU и по формуле (11.11)

∫ a d r = ∫ dU =U (B) −U (A) .

AB AB

100