Matan__teoria

Замечания

1). Полярной системой координат удобно пользоваться, если область интегри(

рования ограничена окружностью или линией ρ = ρ (ϕ ) ,

y

ϕ = β

ρ = ρ 2 (ϕ)

или линией, уравнение которой содержит x

2

+ y

2

.

B

2). Если уравнение линии, ограничивающей область, или

B1

(S)

ϕ = α

x2

y2

ρ = ρ1

(ϕ )

A1

подынтегральная функция содержат a2 + b2 , то удобно

A

x

перейти к обобщенным полярным координатам

0

Рис. 42

x = a ρ cosϕ , y = b ρ sinϕ ;

тогда dS = ab ρ dρ dϕ .

x2

y2 2

2xy

Пример 7.17. Вычислить площадь фигуры, ограниченной линией

+

=

.

a

2

b

2

ab

Решение.

Сначала построим

линию,

исследуя её уравнение.

Выражение

x2

+

y2 2

неотрицательно, значит, и 2 x y

неотрицательно, т.е. линия находится в

a

2

b

2

первой и третьей четвертях. Уравнение линии не изменится при замене x на (−x) и y на (−y) . Значит, эта линия симметрична относительно начала координат и её достаточно построить в первой четверти, а затем воспользоваться симметрией.

Наличие в уравнении линии выражения

x2

+

y2

наводит на мысль восполь(

a

2

b

2

зоваться обобщенными полярными координатами x = a ρ cosϕ , y = b ρ sinϕ .

Тогда

x2

+

y2

= ρ2

и уравнение линии примет вид

a

2

b

2

ρ4 = 2ρ2 sinϕ cosϕ , или ρ2 = sin 2ϕ ,

или ρ = sin 2ϕ .

Как отмечалось, достаточно сначала построить линию в первой четверти, т.е.

для ϕ , принадлежащих отрезку 0, π . Для этого составим следующую таблицу:
				2
	ϕ	0	π 8	2π 8= π 4	3π 8	4π 8 = π 2
	ρ	0	≈ 0,8	1	≈ 0,8	0
Построим точки с вычисленными координатами (ϕ,ρ) , со(								y
единим их плавной линией, которую затем, воспользовав(
шись свойством симметрии, отобразим зеркально относи(											ρ
тельно начала координат (рис. 43). Вычислим площадь S0
											x
той части фигуры, которая расположена в первой четверти:								0
				β ρ2(ϕ)
S0 = ∫ dS = ∫∫ ab ρ dρ dϕ = ab ∫dϕ ∫ ρ dρ .									Рис. 43
	(S0)	(S0)		α ρ1(ϕ)
Чтобы расставить внутренние пределы интегрирования, т.е. пределы изменения
ρ , будем двигаться в области (S0 ) по лучам, выходящим из полюса. На каждом
таком луче ρ меняется от значения ρ = 0 в точке 0 до значения ρ =
									sin 2ϕ на

линии, ограничивающей область (S0 ) . Кроме того, эта область заключена между

61

лучами ϕ = 0 и ϕ = π . Поэтому S0 = ab	π 2	sin 2ϕ
	∫ dϕ	∫ ρ dρ .
2	0	0

Вычислим повторный интеграл, начиная с вычисления внутреннего интеграла

π 2

ρ2

sin2ϕ

π 2

π 2

ab

∫

= ab

∫

sin 2ϕ dϕ = − ab cos2ϕ

, S = 2S0

= ab .

S0

= ab

dϕ

=

2

2

4

0

2

0

0

+∞

0

Пример 7.18. Доказать, что ∫ e−x 2dx =

π .

−∞

Решение. Вычислим вспомогательный интеграл ∫∫ e−x2−y2dxdy для двух областей:

(D)

а) если (D)− круг x2 + y2 ≤ R2 , то, переходя к полярным координатам, получим

		2π	R	2π
∫∫ e−x2− y2dxdy = ∫∫ e−ρ2		ρ dρ dϕ = ∫	dϕ ∫e−ρ2 ρ dρ = − 1	∫
(D)	(D)		2
		0	0	0

	2		R
e−ρ			dϕ = π
			0

	− e	−R	2
1			;

при R → ∞ область (D), расширяясь, заполнит всю плоскость (обозначим ее D∞ ) и

∫∫

e−x2−y2dxdy = lim π

1− e−R 2

= π ;

(D∞)

R→∞

б) если (D)− квадрат −a ≤ x ≤ a,

− a ≤ y ≤ a , то

2

−y

2

a

a

2

−y

2

dy =

a

e−x

2 a

e−y

2

a

e−x

2

2

∫∫

e−x

dxdy =

∫

dx

∫

e−x

∫

dx

∫

dy

=

∫

dx ;

(D)

−a

−a

−a

−a

−a

при a → ∞ область (D), расширяясь, опять заполнит всю плоскость (D∞ ) и

	e−x	2	−y	2	∞		e−x	2	2
∫∫					dxdy =	∫			dx .
(D∞)						−∞

Итак, ∫∫ e−x2−y2dxdy

(D∞)

∞		e−x	2	2
=	∫			dx	= π
	−∞

∞

∫ e−x2dx = π.

−∞

7.5. Тройной интеграл в прямоугольной системе

Вычисление тройного интеграла сводится к вычислению определенного и двойного интегралов. Рассмотрим три случая.

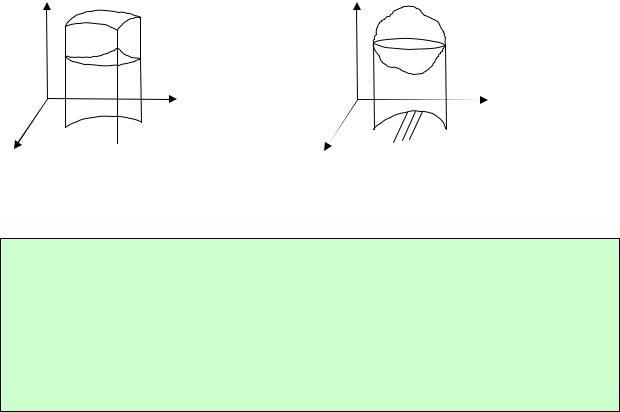
Случай 1. Пусть тело (V) ограничено поверхностями z = z1(x, y), z = z2 (x, y) ,

цилиндрической поверхностью с образующими, параллельными оси OZ (рис. 44,a). Цилиндрическая поверхность может и отсутствовать (рис. 44,б). Тогда

			z2 (x,y)
	∫∫∫ f (x, y, z)dxdydz = ∫∫ dxdy		∫ f (x, y, z)dz.		(7.24)
	(V)	(Vx y)	z1(x,y)
Здесь (Vx y )– есть проекция тела (V)		на плоскость XOY (рис. 44).

Обоснование формулы (7.24) проводится так же, как и для двойного интеграла.

62

zz = z2(x, y)

z = z1(x, y)

y

0

(Vx y )

х

zz = z2(x, y)

z = z1(x, y)

y

0

(Vx y )

х

a)

б)

Рис. 44

Чтобы применять формулу (7.24) на практике, рекомендуем:

1)построить тело (V) ;

2)записать тройной интеграл через повторный интеграл; в повторном ин( теграле сначала расставить внутренние пределы интегрирования, т.е. пре( делы изменения z . При этом переменная интегрирования z меняется от z1(x, y) на нижней поверхности до z2(x, y) на верхней поверхности;

3)вычислить внутренний интеграл при фиксированных x, y ;

4)вычислить внешний интеграл по проекции тела (V) на плоскость XOY .

Случай 2. Пусть тело (V) ограничено поверхностями y = y1(x, z) , y = y2 (x, z) и цилиндрической поверхностью с образующими, параллельными оси OY . Тогда

		y2(x,z)
∫∫∫ f (x, y, z) dxdydz =	∫∫ dxdz	∫ f (x, y, z)dy.	(7.25)
(V)	(Vxz)	y1(x,z)

Случай 3. Пусть тело (V) ограничено поверхностями x = x1(y, z) , x = x2 (y, z) и цилиндрической поверхностью с образующими, параллельными оси OX . Тогда

		x2(y,z)
∫∫∫ f (x, y, z)dxdydz =	∫∫ dydz	∫ f (x, y, z)dx.	(7.26)
(V)	(Vyz)	x1(y,z)

Указания к применению формулы (7.24) с очевидными изменениями перено( сятся и на формулы (7.25), (7.26).

Для вычисления тройных интегралов надо уметь строить поверхности с задан( ными уравнениями. Дадим следующие рекомендации.

1. Если уравнение поверхности не содержит одной переменной, например, уравнение F(x, y) = 0 не содержит z , то поверхность является цилиндрической с образующими, параллельными оси OZ . Сначала строим направляющую с за( данным уравнением F(x, y) = 0, затем через её точки проводим образующие, па( раллельные оси OZ (пример 7.19).

2. Если уравнение поверхности содержит переменные x, y, z , то удобно строить поверхность методом сечения плоскостями x = 0, y = 0, z = 0 или па( раллельными им плоскостями (пример 7.20).

63

	Пример 7.19. Найти объём тела, ограниченного				z
	поверхностями y = −	x ,	y = 0, x + z = 3, x + 3z = 3 .		A
	Решение. Построим	поверхности, ограничиваю(
					(σ2)
	щие тело. В уравнении y = − x отсутствует z ,
					D
	следовательно, это уравнение определяет цилин(			(σ1)	O	y
	дрическую поверхность с образующими, парал(
	лельными оси OZ . Направляющая в плоскости
	XOY имеет уравнение		y = − x (или y2 = x , y ≤ 0 ),	C	B
	которое определяет левую часть параболы. Строя
				x	Рис. 45
	направляющую и образующие, проходящие через
	её точки (рис. 45), получим цилиндрическую поверхность (σ1) . Уравнение y = 0
	определяет плоскость XOZ .
	Следующее уравнение x + z = 3 есть уравнение первой степени, значит,
	оно определяет плоскость. В уравнении отсутствует			y , значит, плоскость па(
	раллельна оси OY . Кроме того, при x = 0 имеем z = 3 , при z = 0 имеем x = 3. Че(
	рез полученные две точки A и B проводим плоскость (σ 2 ) , параллельную оси
	OY . Эта плоскость пересечет плоскость XOZ по отрезку AB , а цилиндрическую
	поверхность – по дуге		AC (рис. 45).
	Аналогично, уравнение x + 3z = 3 определяет плоскость, параллельную оси
	OY , пересекающую плоскость XOZ по отрезку BD, а цилиндрическую поверх(
	ность – по дуге DC .
	Объём тела, ограниченного рассмотренными поверхностями, найдем по од(
	ной из формул (6.6):

V = ∫ dV = ∫∫∫dxdydz .

(V) (V)

Запишем тройной интеграл через повторный по формуле (7.24). Чтобы расста( вить внутренние пределы интегрирования, т.е. пределы изменения z , будем дви(

гаться параллельно оси OZ . При этом z						меняется от	z =	3− x			на плоскости BDC
									3
до z =3−x на плоскости ABC . Поэтому
	∫		3−x		∫∫		3		∫∫		(3− x)dxdy .
			∫
V =		dxdy		dz =	(3− x)	− (3− x)/3 dxdy = 2
	(Vx y)		(3−x) 3		(Vx y)				(Vx y)

Здесь (Vx y ) есть проекция тела (V ) на плоскость XOY , т.е. криволинейный тре(

угольник OBC . Вычислим теперь двойной интеграл. Для этого запишем его че( рез повторный интеграл с внутренним интегрированием по y . Для выяснения пределов изменения y будем двигаться в области OBC параллельно оси OY . При этом y меняется от y = − x на дуге OC до y = 0 на отрезке OB . Поэтому

30

V =	2	∫dx	∫ (3− x)dy .
3

0− x

64

dxdz = dS

x2 + z2 на ρ2 , а

Вычисляя сначала внутренний интеграл при фиксированном x , а затем внеш(
ний интеграл, получим																	z
3											3
													8	3
2		2	x	3 2	2	− x	5 2			2		=
V = 3 ∫(3− x) x dx = 3 (3					3					5)	0			5		.			(V)
0
Пример 7.20. Найти центр тяжести тела, ограни(
ченного поверхностями			x2 + z2 = y ,					y = 4.									0	C	4	y
Решение. Построим поверхности, ограничивающие
тело. Первую поверхность с уравнением x2 + z2 = y																	x	Рис. 46
построим методом сечений. В сечении плоскостью																	x = 0	получим параболу
z2 = y с осью симметрии – осью OY (рис. 46). В сечении плоскостью y = 4 полу(
чим окружность		x2 + z2 = 4. По этим сечениям видно, что уравнение																	x2 + z2 = y

определяет параболоид. Вторая поверхность – плоскость y = 4 – отсекает от па( раболоида его часть, изображенную на рис. 46.

Центр тяжести полученного однородного тела, в силу его симметрии, нахо( дится на оси OY (в точке C ). Следовательно, xc = zc = 0 . Координату yc центра тяжести тела найдем с помощью тройных интегралов по формулам (6.9) и (6.7):

yc =	1	∫ γ ydV , где	m = ∫γ dV .
	m
		(V)	(V )

Так как тело однородное, то его плотность γ является постоянной величиной и её можно вынести за знак интеграла. Поэтому

	γ ∫	ydV		∫	ydV
y =	(V)		=	(V)		=	I1	.
c	γ ∫	dV		∫	dV I2
	(V)			(V)

Вычислим сначала интеграл I1 , стоящий в числителе; для этого запишем его в виде повторного интеграла с внутренним интегрированием по y . Для выяснения пределов изменения y будем двигаться параллельно оси OY . При этом y меня( ется от y = x2 + z2 на поверхности параболоида до y = 4 на плоскости. Поэтому

4

I1 = ∫

y dV = ∫∫∫ y dxdy dz = ∫∫

dx dz

∫ y dy.

(V)

(V)

(Vxz)

x2+z2

Сначала вычислим внутренний интеграл

y

2

4

2

I1

= ∫∫ dxdz

= 1

∫∫ 16− (x2

+ z2) dxdz .

(Vxz)

2

x2+z2

2

(Vxz)

Так как проекция (Vxz ) тела (V)

на плоскости XOZ есть круг, то получившийся

двойной интеграл удобно вычислять в полярной системе координат, заменяя на ρ dρdϕ . Тогда получим

I1	= 1	∫∫	16 − ρ4 ρ dρ dϕ .
	2	(Vxz)

Двойной интеграл запишем через повторный с внутренним интегрированием по ρ .

65

Так как сечение параболоида x2 + z2 = y плоскостью y = 4 есть окружность x2 + z2 = 4 радиуса 2 , то ρ меняется от 0 до 2 ; ϕ меняется от 0 до 2π и, следовательно,

					2π		2			2π							6			2			2π
				= 1	∫ dϕ ∫(16 − ρ4)ρ dρ = 1						∫ dϕ					ρ						= 32	∫ dϕ = 64π .
	I1											8ρ2			−
				2	0		0			2	0				6					0		3	0	3
Аналогично вычисляется интеграл I2 :
												4										4 − (x2 + z2 ) dxdz =
			I2 = ∫ dV = ∫∫∫ dx dy dz =							∫∫	dx dz	∫			dy =			∫∫
					(V)			(V)		(Vxz)	x2+ z2						(Vxz)
								2		2π	2		2							2π			2	ρ4			2
			= ∫∫				− ρ			∫ dϕ ∫(4 − ρ				)ρ dρ = ∫ dϕ 2ρ −													= 8π .
						4			ρ dρ dϕ =
				(Vxz)						0	0										0			4			0
Итак, yc =	I1			= 8	и центр тяжести данного тела находится в точке C (0,																							8	, 0).
	I	2		3																								3

7.6. Тройной интеграл в криволинейной системе

Для вычисления тройного интеграла иногда удобно использовать не пря( моугольные координаты (x, y, z), а некоторые криволинейные координаты

(u,v,w). Пусть известна связь между этими координатами

D(x, y, z)

x′

x′

x′

x = x(u,v,w), y = y(u,v,w), z = z(u,v,w) и

u

v

w

=

y′

y′

y′

≠ 0 .

D(u,v,w)

u

v

w

′

′

′

z

z

v

z

w

u

Аналогично случаю двойного интеграла можно показать, что

dV = dxdydz =

D(x, y, z)

du dvdw,

(7.27)

D(u,v,w)

∫∫∫ f (x, y, z)dxdy dz = ∫∫∫ f (x(u,v,w), y(u,v,w), z(u,v,w))

D(x, y, z)

du dvdw.

(7.28)

D(u,v, z)

( )

(V

)

V

Здесь (V ) и (V ) ─ области изменения соответственно переменных (x, y, z) и (u,v,w).

Для вычисления тройного интеграла ∫		f (P)dV = ∫ f (x, y, z)dV следует
	(V)		(V)
1) заменить x, y, z,	dV на их выражения в криволинейной системе координат,
x = x(u,v,w),	y = y(u,v,w), z = z(u,v,w),	dV =		D(x, y, z)			dudvdw;
				D(u,v,w)

2) заменить область (V ) изменения переменных (x, y, z) на область (V )

изменения переменных (u,v,w).

66

	Замечание.Иногда удобнее вычислить не якобиан	D(x, y, z)	= I, а якобиан	D(u,v,w)	= I .
		D(u,v,w)		D(x, y, z)
					1

Тогда искомый якобиан I = 1 .

I1

Пример 7.21. Вычислить объем параллелепипеда, ограниченного плоскостями

a1 x + b1 y + c1 z = ± h1, a2 x + b2 y + c2 z = ± h2 , a3 x + b3 y + c3 z = ± h3.

Решение. Введем новые переменные

u = a1 x + b1 y + c1 z,

v = a2 x + b2 y + c2 z, w = a3 x + b3 y + c3 z

D(u,v,w)

u′

u′

u′

a

b

c

x

y

z

1

1

1

и вычислим якобиан

=

=

v′

v′

v′

=

a

b

c

.

D(x, y, z)

x

y

z

2

2

2

w′

w′

w′

a

b

c

x

y

z

3

3

3

Тогда искомый объем равен

D(x, y, z)

1

h1

h2

h3

8h1h2

h3

V = ∫

dV = ∫∫∫ dxdy dz = ∫∫∫

du dvdw =

∫ du ∫

dv ∫ dw =

.

D(u,v, z)

(V )

(V )

(V )

−h1

−h2

−h3

Тройной интеграл в цилиндрических координатах

Положение точки M (x, y, z)

в пространстве можно охарактеризовать с помо(

щью цилиндрических координат (ρ,ϕ, z), где ρ,ϕ − полярные координаты про(

екции точки M на плоскость XOY,

z − аппликата точки M . Поэтому аналогич(

но полярной системе координат

x = ρ cosϕ ,

y = ρ sinϕ ,

z = z.

(7.29)

x′

x′

x′

cosϕ

−ρ sinϕ

0

D(x, y, z)

ρ

ϕ

z

Вычислим якобиан

=

y′

y′

y′

=

sinϕ

ρ cosϕ

0

= ρ .

D(ρ,ϕ, z)

ρ

ϕ

z

z′

z′

z′

0

0

1

ρ

ϕ

z

Тогда элемент объема в цилиндрических координатах

dV = ρ dρ dϕ dz

.

(7.30)

Для вычисления тройного интеграла ∫

f (P)dV = ∫

f (x, y, z)dV следует

(V)

(V)

1) заменить x, y, z, dV на их выражения в цилиндрической системе координат,

x = ρ cosϕ , y = ρ sinϕ ,

z = z ,

dV = ρ dρ dϕ dz ;

2) заменить область (V ) изменения переменных (x, y, z)

на область (V ) из(

менения переменных (ρ,ϕ, z).

Замечания

1). К цилиндрическим координатам целесообразно переходить, когда уравнение поверхностей, ограничивающих тело, содержит x2 + y2 .

2). Внутреннее интегрирование обычно удобно вести по z .

67

Пример 7.22. Вычислить массу тела, ограниченного поверхностями z = 6 − x2 − y2, z = x2 + y2 , если плотность γ = z.

Решение. Поверхность z = 6 − x2 − y2 строим методом сечений:

	x = 0,			z = 0,			Получаем параболоид (рис. 47).
	2		2		2
z = 6 − y ,		x		+ y		= 6.

z

6

Поверхность				z = x2 + y2 также строим методом сечений
x = 0,				z =1,		Получаем конус (рис. 47).			y
z =			x2 + y2					O
	y	,			= 1.		x
В цилиндрической						системе координат уравнения этих по(		Рис. 47

верхностей имеют более простой вид: z = 6 − ρ2, z = ρ2 = ρ .

Решив систему из этих двух уравнений, найдем пересечение этих поверхностей ─ окружность ρ = 2.

Вычислим массу тела, используя для вычисления интеграла цилиндриче(

скую систему координат, учитывая, что

dV = ρ dρ dϕ dz , внутреннее интегри(

рование ─ по z , причем на прямой, параллельной оси OZ , z

меняется от

z = ρ

на конусе до z = 6− ρ2

на поверхности параболоида (рис. 47):

6− ρ2

2π

2

m = ∫ γ dV =∫∫∫z ρ dρ dϕ dz =

∫∫

ρ dρ dϕ ∫

z dz = 12 ∫ dϕ ∫ (6 − ρ2)2 − ρ2 ρ dρ = 923 π .

(V )

(V )

(Vx y)

ρ

0

0

Тройной интеграл в сферических координатах

Положение точки M (x, y, z)

в пространстве можно оха(

z

рактеризовать с помощью сферических координат (r,θ,ϕ) ,

r

M

где r − длина радиус(вектора точки M (рис. 48), θ − угол

отклонения радиус(вектора точки M от оси OZ (0 ≤ θ ≤ π ),

θ

ϕ − угол отклонения проекции на плоскость XOY радиус(

0

ϕ

y

вектора точки M от оси OX

(0 ≤ ϕ ≤ 2π ).

x

P

Установим связь между прямоугольными и сфериче(

Рис. 48

скими координатами. Из прямоугольного треугольника

OMP имеем OP = r sinθ , z = MP = r cosθ . Так как x = OP cosϕ ,

y = OP sinϕ , то

x = rsinθ cosϕ ,

y = rsinθ sinϕ ,

z = r cosθ ;

x2 + y2 + z2 = r2.

(7.31)

Вычислим якобиан

x′

x′

x′

sinθ cosϕ

r cosθ cosϕ − r sinθ sinϕ

D(x, y, z)

r

θ

ϕ

=

y′

y′

y′

=

sinθ sinϕ

r cosθ sinϕ

r sinθ cosϕ

.

D(r,θ,ϕ )

r

θ

ϕ

z′

z′

z′

cosθ

− rsinθ

0

r

θ

ϕ

Раскроем определитель по элементам третьей строки

D(x, y,z)

rcosθ cosϕ − rsinθ sinϕ

sinθ cosϕ − rsinθ sinϕ

= cosθ

rsinθ cosϕ

+ rsinθ

sinθ sinϕ

rsinθ cosϕ

=

D(r,θ,ϕ )

rcosθ sinϕ

68

= r2sinθ cos2θ + r2 sin3θ = r2sinθ (cos2θ + sin2θ )= r2sinθ > 0.

Тогда элемент объема в сферических координатах

dV = r2 sinθ dr dθ dϕ .

(7.32)

Для вычисления тройного интеграла ∫ f (P)dV = ∫ f (x, y, z)dV следует

(V) (V)

1) заменить x, y, z, dV на их выражения в сферической системе координат, x = rsinθ cosϕ , y = rsinθ sinϕ , z = r cosθ, x2 + y2 + z2 = r2, dV = r2 sinθ drdθ dϕ ; 2) заменить область (V ) изменения переменных (x, y, z) на область (V )

изменения переменных (r,θ,ϕ) .

Замечания

1). К сферическим координатам целесообразно переходить, когда тело ограни( чено сферой r = const , конусом θ = const или поверхностью, уравнение которой содержит x2 + y2 + z2 .

2). Тройной интеграл следует записать в виде трехкратного с интегралами (сле( ва направо) по ϕ , θ , r.

3). Сначала расставить пределы интегрирования по r (двигаясь по лучу из начала координат), потом ─ по θ (двигаясь от оси OZ ), потом ─ по ϕ .

4). Если уравнение границы области или подынтегральная функция содержат

x2

+

y2

+

z2

, то следует перейти к обобщенным сферическим координатам

2

2

a

b

2

c

тогда

x2

+

y2

+

z2

= r2

,

x = a rsinθ cosϕ , y = b rsinθ sinϕ , z = c r cosθ ;

2

a

b

2

c

2

dV = abc r2 sinθ dr dθ dϕ.

(7.33)

Пример 7.23. Вычислить момент инерции относительно плоскости XOY одно(

родного

(с плотностью

γ ) тела, ограниченного

поверхностями

x2 + y2 + z2 = R2, x2 + y2 = 3z2 (z ≥ 0).

Решение. Момент инерции тела вычислим по формуле (6.10)

Ixy = ∫ z2 γ dV = γ ∫ z2 dV.			z
(V )	(V )
Так как тело ограничено сферой и конусом (рис. 49), то пе(
рейдем к сферическим координатам. При этом, учитывая
формулы (7.30), уравнение сферы примет вид		r2 = R2 или	о	y
r = R ; уравнение конуса примет вид
r2 sin2θ cos2ϕ + r2 sin2θ sin2ϕ = 3r2 cos2θ , или tg2θ = 3,		или θ = π .	x
		3

Рис. 49

Используя формулы (7.30) и (7.31), получим

69

			2π	π /	3	R
	Ixy = γ ∫	z2 dV = γ ∫∫∫r2 cos2θ r2 sinθ dr dθ dϕ = −γ	∫ dϕ ∫			cos2θ d cosθ ∫r4dr =	7	π γ R 5.
							60
	(V )	(V )	0	0		0

Пример 7.24. Найти объем тела, ограниченного поверхностью

x2

+

y2

+ z2 3

x2

+

y2

= z2 (z ≥ 0).

4

9

4

9

Решение. Перейдем к обобщенным сферическим координатам

x = 2rsinθ cosϕ ,

y = 3rsinθ sinϕ ,

z = r cosθ . В этих координатах

x2

+

y2

+ z2

= r2

,

x2

+

y2

= r2 sin2θ (cos2ϕ + sin2ϕ )= r2 sin2θ

4

4

9

9

и уравнение поверхности примет вид

x

r6 r2 sin2θ = r2 cos2θ или r = 3 ctgθ .

z

оy

					Рис. 50
По условию z ≥ 0 , поэтому ct gθ ≥ 0 и θ (0,π / 2]. Cоставим таблицу:
	θ	0	π / 4	π 2
	r	∞	1	0

Построим точки с вычисленными координатами (r,θ,ϕ) сначала при ϕ = π / 2, т.е. в плоскости YOZ (рис. 50). Так как уравнение поверхности r = 3 ct gθ от ϕ не зави( сит, то при любом ϕ получим такую же линию; все эти линии образуют поверх( ность вращения (рис. 50). Объем тела, ограниченного этой поверхностью, вы( числим с учетом соотношения (7.33) при a = 2, b = 3, c =1:

V = ∫	dV = ∫∫∫2 3 r2 sinθ dr dθ dϕ .
(V )	(V )

Чтобы расставить пределы изменения r , будем двигаться в области (V ) по лучам, выходящим из начала координат. На каждом таком луче r меняется от значе(

ния r = 0 в начале координат до значения r = 3 ctgθ							на поверхности, ограничи(
вающей область (V ). Кроме того, эта область заключена между лучами θ = 0 и
θ = π / 2 , ϕ [0,2π ] . Поэтому
2π				2π
	π / 2	3	ctgθ			π / 2
V = 6 ∫ dϕ	∫ sinθ dθ		∫	r2 d r = 2 ∫ dϕ		∫ sinθ ct gθ dθ = 4π .
0	0	0		0		0	=cosθ
7.7. Поверхностный интеграл первого рода
Вычисление поверхностного интеграла 1 рода							∫ f (P)dσ сводится к вычис(
							(σ)

лению двойного интеграла. Рассмотрим несколько случаев.

Случай 1. Пусть гладкая поверхность (σ ) задана параметрическими уравнениями

x = x(u,v), y = y(u,v), z = z(u,v) или r = r (u,v), (u,v) (S) .

По определению, поверхностный интеграл функции f (P) по поверхности (σ )

есть предел интегральной суммы функции f (P) , который не зависит от способа разбиения поверхности (σ ) на ячейки:

70