Учебник

9. Преобразования систем координат

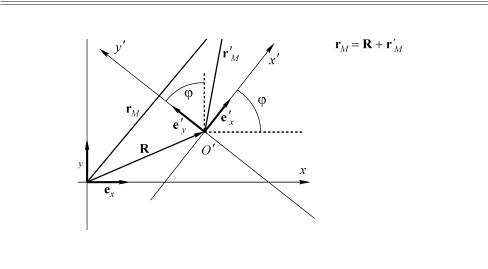
Аналогичная ситуация возникает и при описании точек в разных системах отсчета. На рис. 9.2 приведен пример точки M и трех систем отсчета, повернутых и сдвинутых относительно друг друга. Мы видим, что в системе отсчета K у точки M обе координаты не равны нулю. В системе отсчета K′ абсцисса точки M равна нулю xM′ = 0, а в системе отсчета K′′ уже обе координаты равны нулю. При этом точка M осталась геометрически на прежнем месте. Следовательно, между координатами точки в различных системах отсчета, как и у координат вектора, должна быть определенная связь, которая должна определяться тем, как связаны между собой системы координат.

9.2. Связь между координатами точки в различных системах координат

Предположим, что нам задана точка			M (x, y) своими коор-
динатами в системе отсчета K. А также задана вторая система
координат K′ — новая система отсчета, которая получена из
старой системы	отсчета K	после параллельного переноса на
заданный вектор	R = ( X0 ,Y0 )	и поворота на заданный угол ϕ
(ñì. ðèñ. 9.3.):
Вектор R связывает между собой радиус-векторы точки M
в новой и в старой системах отсчета
	rM = R +rM′ .		(9.1)

Это соотношение поможет нам найти связь и между координатами.

Представим векторы rM è R в виде их разложений по ортам системы K :

rM = xex + yey è R = X0ex +Y0ey ,

а вектор rM′ разложим по базису новой системы отсчета K ′:

rM′ = x′e′x + y′e′y .

143

I. Векторная алгебра

Ðèñ. 9.3. Связь между радиус-векторами точки в различных системах отсчета

Здесь коэффициенты x′ è y′ — не что иное, как координаты точки M в системе отсчета K ′, то есть искомые новые координаты. Теперь подставим эти разложения в соотношение (9.1):

xex + yey = X0ex +Y0ey + x′e′x + y′e′y .

(9.2)

Дальше можно рассуждать двумя способами, которые, естественно, приводят к одному результату.

Способ 1

Умножим соотношение (9.2) поочередно на векторы ex è ey , и воспользуемся соотношениями, справедливыми для ортов в ортонормированных базисах: exex = eyey =1 è exey = eyex = 0. Тогда из (9.2) получим два соотношения для координат:

x = X0 + x′(exe′x ) + y′(exe′y ) ,

y =Y0 + x′(eye′x ) + y′(eye′y ) .

144

9. Преобразования систем координат

Скалярные произведения ортов в этих соотношениях равны косинусам углов между векторами, так как длины ортов равны единице. Например, exe′x = cos( exe′x ). Углы же между ортами можно вязать с заданным углом поворота ϕ. Так, например, угол между первыми базисными векторами просто равен ϕ. Таким образом, для скалярных произведений ортов старого и нового базисов получаем следующие соотношения:

exe′x = cosϕ , exe′y = cos π2 +ϕ = −sinϕ ,

π			= sinϕ ,	eye′y = cosϕ ,	(9.3)
eye′x = cos	2	−ϕ

с помощью которых получаем окончательные выражения для связи координат:

x = X0	+ x′cosϕ − y′sinϕ	.	(9.4)
	+ x′sinϕ + y′cosϕ
y =Y0

Полученное выражение называется законом преобразования

координат.
Способ 2
В выражение (9.2) входят векторы e′x							è e′y ,	заданные в двумер-
ном пространстве с базисом	(ex ,ey ). Следовательно, их можно
представить в виде разложения по этому базису:
e′ =α		e		+α		e	y ,	(9.5)
x	xx		x		xy
e′y =α yxex +α yyey

где коэффициенты αij являются координатами ортов нового базиса в старом базисе. Эти же выражения (9.5) можно трактовать как закон преобразования базисных векторов.

Коэффициенты αij находим так же, как и координаты любого вектора в базисе — путем скалярного произведения этого вектора на соответствующий орт:

αij = e′ie j .

Такие скалярные произведения мы только что вычислили в (9.3) и поэтому для новых ортов получаем:

145

I. Векторная алгебра

e′	= e		cosϕ +e		sinϕ	.	(9.6)
x		x		y
e′y	= −ex sinϕ +ey cosϕ

Теперь нам осталось подставить эти выражения в (9.2):

xex + yey = X0ex +Y0ey + x′(ex cosϕ +ey sinϕ )+ y′(−ex sinϕ +ey cosϕ )

и приравнять между собой коэффициенты перед ортами ex è ey в правой и левой части этого равенства. В итоге получим соотношения

x = X0 + x′cosϕ − y′sinϕ ,

y =Y0 + x′sinϕ + y′cosϕ

которые совпадают с результатом (9.4).

Оба вышеприведенных вывода могут рассматриваться как доказательство теоремы о линейности преобразований координат при параллельных переносах и поворотах систем координат.

Теорема о линейности преобразований координат

При переходе от одной декартовой системы координат к другой путем параллельного переноса и поворота, координаты выражаются друг через друга линейным образом.

Только что мы получили так называемые формулы перехода от одной декартовой системы отсчета к другой при параллельном переносе начал отсчета на вектор ( X0 ,Y0 ) и поворота на угол ϕ :

x = X0	+ x′cosϕ − y′sinϕ	.	(9.4)
	+ x′sinϕ + y′cosϕ
y =Y0

Несмотря на то, что эти соотношения не дают явных выражений для новых координат, они описывают так называемый

переход от старых координат к новым. Дело в том, что они позволяют любую функцию старых координат, заданную в старой системе отсчета, выразить через новые координаты, например:

f (x, y) = f (x(x′, y′), y(x′, y′)) ≡ f ′(x′, y′).

Для того чтобы выразить новые координаты через старые, нужно провести так называемое обратное преобразование ко-

146

9. Преобразования систем координат

ординат. С этой целью можно умножить основное равенство (9.2) поочередно на орты нового базиса и получить явные выражения для новых координат x′ = x′(x, y) è y′ = y′(x, y).

Однако, такую связь можно получить и из соотношений (9.4), если рассмотреть их как систему уравнений относительно двух переменных x′ è y′. Решение такой системы дает закон обратного преобразования координат:

	x′ = (x − X0 ) cosϕ +(y −Y0 ) sinϕ
			.	(9.7)
		0 ) sinϕ +(y −Y0 ) cosϕ
y′ = −(x − X

Интересным является тот факт, что в случае поворота соотношения (9.7) можно получить из (9.4) без вычислений, если учесть, что обратное преобразование можно трактовать как поворот в противоположную сторону, то есть просто заменить ϕ → −ϕ.

9.3. Преобразования координат в пространстве

Теперь рассмотрим преобразование координат точки в трехмерном пространстве. Предположим, что в старой системе от- счета K задан радиус-вектор R = ( X1 , X2 , X3 ) начала отсчета и базисные векторы (e1′,e′2 ,e′2 ) новой системы координат K ′:

3
e′i = ∑αik ek .	(9.8)

k =1

Эти выражения с одной стороны можно трактовать как разложение новых базисных векторов по старому базису, а с другой стороны, как закон преобразования базиса при вращениях в трехмерном пространстве.

Радиус-вектор rM заданной точки M , как и в двумерной задаче, можно представить в следующем виде: rM = R +rM′ , ãäå rM′ — это радиус-вектор точки M в новой системе отсчета, и поэтому его координаты являются новыми координатами точки M .

Умножая это соотношение поочередно на базисные векторы старого базиса ek , получим искомые выражения старых координат через новые:

147

I. Векторная алгебра

′	Xk		3	′ ′		3	′	3
xk ≡ rM ek = (R +rM )ek =		+	∑xiei		ek = Xk + ∑xi			∑αije jek =
		i=1				m=1		j=1
3	3					3
= Xk + ∑∑xi′αijδ jk =Xk + ∑xi′αik .
i=1	j=1					m=1

Мы получили аналогичное (9.4) выражение для преобразования координат в трехмерном пространстве:

3
xk = Xk + ∑xi′αik ,	(9.9)
i=1
ãäå αik = eiek ≡ cos( eiek ) — косинусы углов	между соответ-
ствующими ортами.

Полученное соотношение имеет одно существенное (и очень важное) отличие от формулы преобразования ортов. В формуле преобразования ортов суммирование ведется по второму индексу коэффициентов αik , а в формуле преобразований координат — по первому. Такое отличие особенно будет важным в будущем при изучении неэвклидовых пространств.

Âнашем случае это отличие приводит к тому, что в формулах прямого преобразования (9.4) знак «минус» стоит в первом уравнении, а в формулах для обратного преобразования (9.7) знак минус стоит во втором уравнении.

Âдвумерном случае нам удалось углы между всеми ортами выразить через угол поворота (9.3). В трехмерном случае возможны различные способы описания поворотов систем отсчета, с которыми можно познакомиться в различных учебниках по геометрии или физике.

9.4.Преобразования векторов.

Новое определение вектора

Теперь рассмотрим преобразования координат векторов при поворотах системы отсчета, или, другими словами, при переходе от одного базиса к другому.

148

9. Преобразования систем координат

Предположим, что задан			вектор			a		своими координатами
1 2	( 1	2 )	À	также				даны базисные векторы
a = (a , a ) в базисе	e ,e	.
нового базиса:
	e′ =α e +α				12	e	2 .
		1	11	1
	e′2 =α 21e1 +α 22e2

Тогда можно совершить переход к новому базису:

a = a1e1 + a2e2 ≡ a1′e1′ + a2′e′2 = a1′(α11e1 +α12e2 )+ a2′(α 21e1 +α 22e2 ). (9.10)

Раскрывая скобки и сравнивая коэффициенты, перед соответствующими ортами, получаем следующие формулы для преобразования координат векторов:

a =α a′	+α a′	(9.11)
1 11 1	21 2 .
a2 =α12a1′+α 22a2′

Мы видим, что координаты вектора меняются по тому же закону, что и координаты точки при поворотах. В этом нет ниче- го удивительного, так как координаты точки, по сути, являются координатами радиус-вектора этой точки, и мы могли получить формулы (9.11) прямо из соотношений (9.9). Таким образом, в случае поворотов координаты вектора преобразуются по следующему закону:

a = a′cosϕ −a′sinϕ			.	(9.12)
1	1	2
a2	= a1′sinϕ + a2′ cosϕ

Давайте найдем квадрат длины вектора в старом и в новом базисе:

a2 = a12 + a22 = (a1′cosϕ − a2′sinϕ )2 + (a1′sinϕ + a2′ cosϕ )2 ≡ (a1′)2 +(a2′)2 .

Мы видим, что длина вектора не изменяется при переходе от одного базиса к другому, и, кроме того, выражается одинаковым образом через координаты в различных базисах. Такие величины называются инвариантами èëè скалярами.

149

I. Векторная алгебра

Другим примером скалярной величины является скалярное произведение. Вычислим скалярное произведение двух векторов в разных базисах:

ab = a1 b1 + a2b2 = (a1′cosϕ − a2′ sinϕ )(b1′cosϕ −b2′sinϕ ) +

+(a1′sinϕ + a2′ cosϕ )(b1′sinϕ +b2′cosϕ ) = a1′ b1′ + a2′ b2′ .

Тот факт, что результатом скалярного произведения векторов является скалярная величина, и послужил причиной, по которой это произведение назвали скалярным произведением.

В трехмерном пространстве формулы преобразования координат векторов тоже совпадают с формулами (9.11) преобразования координат вектора в плоскости:

ai = ∑α kiak′,	(9.13)
k

где число αik является координатой орта нового базиса e′i , соответствующей орту старого базиса ek :

ei = ∑αike′k . k

В этих соотношениях намеренно не поставлены пределы суммирования по компонентам, потому что эти формулы справедливы в пространствах с любой размерностью. Именно изучение преобразования векторов позволяет нам обобщить понятие вектора для пространств любой размерности и на объекты любой математической или физической природы, которые уже трудно представить в виде направленных отрезков.

Напомним, что в начале нашего курса вместо «школьного» геометрического определения вектора как направленного отрезка, который определяет «направление и расстояние», было введено понятие вектора как класса эквивалентности равных направленных отрезков, которые изучает аналитическая геометрия. Теперь мы можем перейти к еще более абстрактному понятию

150

9. Преобразования систем координат

вектора, вообще не связанному с геометрическими понятиями. А именно, можно определить вектор как упорядоченный набор чисел в некотором базисе. Причем главным в этом определении будет то, что эти числа изменяются при переходе от одного базиса к другому по определенному закону (9.13):

ai = ∑α kiak′. k

Как мы уже неоднократно отмечали, координатами ai в обобщенном определении вектора может быть что угодно — абсцисса или ордината точек в декартовом пространстве, коэффициент в разложении решения дифференциального уравнения, например, уравнения теплопроводности, по простым решениям, количество химического реагента, амплитуда вероятности состояния в квантовой теории поля, соответствующая какой-то новой элементарной частице, относительное количество красного цвета

âсиреневом цвете, и даже время в теории относительности. Исследованию таких векторов и пространств, в которых за-

даны такие векторы, будут посвящены последующие разделы высшей математики и физики.

Там также будут встречаться некоторые сложные понятия и объекты, которые можно рассмотреть и с точки зрения обычных векторов в аналитической геометрии. Теперь, в качестве дополнительного материала, мы рассмотрим некоторые из таких понятий.

9.5.Преобразования координат при переходе

всистему отсчета с другой ориентацией. Собственные и несобственные преобразования

Как вы уже знаете, системы координат могут отличаться друг от друга не только поворотом и переносом начала координат, но и ориентацией. На рис. 9.4 а приведены примеры таких преобразований.

Простейшим примером перехода от системы отсчета с правым базисом к системе отсчета с левым базисом является смена

151

I. Векторная алгебра

направления одной из осей координат (см. рис. 9.4 б). Например, если новая система может отличаться от старой лишь переменой направлений оси ординат:

O → O′ = O

K → K′: ex →e′x = ex . (9.14)ey → e′y = −ey

à)

á)

Ðèñ. 9.4. Переход между системами с различной ориентацией

Такое преобразование системы координат похоже на отражение в зеркале, поэтому их так и называют зеркальными преобразованиями. Главная их особенность заключается в том, что их невозможно свести к какой-нибудь последовательности поворотов.

Нарисуйте на бумаге систему координат, и вы увидите, что повороты можно производить, не выводя лист бумаги из той плоскости, в которой он изначально находился. А для того, чтобы перевести нарисованную систему в систему с противоположной ориентацией, вам обязательно придется перевернуть лист вокруг какой-нибудь из прямых, лежащих на листе.

По этой причине нельзя пользоваться для этих преобразований формулами перехода (9.4) и (9.7), содержащими угол поворота. Однако те же соотношения можно записать в более общем виде, аналогичном (9.9):

152