Учебник

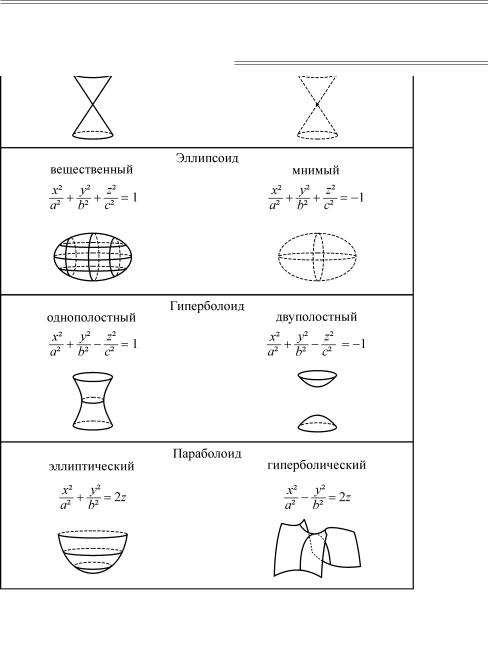
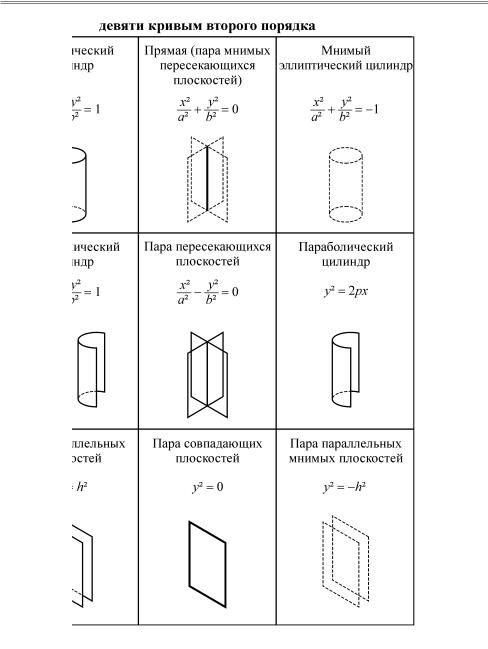
22. Поверхности второго порядка

При вращении этой гиперболы вокруг оси OZ					мы получим
поверхность с уравнением
	x2 + y2	−	z2	= −1.	(22.17)
	b2		c2

Ðèñ. 22.2. Однополостный и двуполостный гиперболоиды

Последующее сжатие вдоль оси OX приводит это уравнение к общей форме канонического уравнения двуполостных гиперболоидов:

	x2	+	y2	−	z2	= −1.	(22.18)
	a2		b2		c2

Горизонтальными сечениями обоих гиперболоидов являются эллипсы:

x2

+

y2

−

z2

= ±1,

z = z

x2

+

y2

= ±1+

z2

. (22.19)

0

0

a2

b2

c2

a2

b2

c2

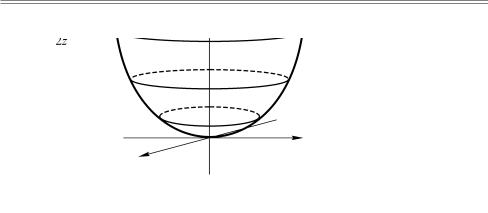
Причем у однополостного гиперболоида такое сечение всегда существует, и наименьшие размеры имеет эллипс, который является пресечением гиперболоида и плоскости XOY. Он получил название горловой эллипс. А у двуполостного гиперболоида есть область z < c, в которой гиперболоид не имеет точек. Значит, он состоит из двух разделенных частей, каждая из которых является границей некоторой полости. Поэтому эта поверхность называется двуполостным гиперболоидом.

343

III. Кривые и поверхности второго порядка

Если эти однополостный и двуполостный гиперболоиды построены вращением сопряженных гипербол, то они называются сопряженными гиперболоидами. Асимптоты сопряженных гипербол при таком вращении переходят в конус с уравнением x2 / a2 + y2 / b2 = z2 / c2 , который делит пространство на две части, каждая из которых содержит только один из гиперболоидов. Более того, при удалении от начала координат оба гиперболоида стремятся к этому конусу, поэтому такой конус называется

асимптотическим.

22.4. Параболоиды

Для изучения параболоидов особенно хорошо подходит метод сечений. Рассмотрим, например, эллиптический параболоид

	x2	+	y2	= 2z.	(22.20)
	a2		b2

Горизонтальные сечения его оказываются эллипсами:

x2

+

y2

= 2z,

z = z

x2

+

y2

= 2z

.

(22.21)

a2

b2

0

a2

b2

0

Причем существуют они только при положительных значе- ниях z. Сечения вертикальными плоскостями являются параболами. Например, сечение плоскостью XOZ (y = 0) дается уравнением

x2	+	y2	= 2z,	y = 0	x	2	= 2a	2	z.	(22.22)
a2		b2

В принципе, эллиптический параболоид можно было исследовать аналогично гиперболоидам путем вращения параболы y2 = 2b2 z, заданной в плоскости YOZ. Полученная в итоге такого вращения поверхность называется параболоид вращения, и описывается уравнением x2 + y2 = 2b2 z. Последующее его сжатие вдоль оси OX èëè OY позволяет получить произвольный эллиптический параболоид.

344

22. Поверхности второго порядка

Ðèñ. 22.3. Эллиптический параболоид

Однако, такой метод не подходит к описанию гиперболического параболоида, который задан уравнением

	x2	−	y2	= 2z.	(22.23)
	a2		b2

Его форму можно исследовать только методом сечений.

Сначала построим сечение этой поверхности плоскостью

XOZ (y = 0):

	x2	−	y2	= 2z, y = 0	x2	= 2z.	(22.24)
	a2		b2		a2

Значит, в плоскости XOZ кривая пересечения является параболой, направленной вверх. Если мы рассмотрим пересечение параболоида с плоскостью YOZ (x = 0), то мы получим параболы, ветви которых направлены вниз.

	x2	−	y2	= 2z, x = 0	y2	= −2z.	(22.25)
	a2		b2		b2

Пересечения параболоида с другими плоскостями x = x0 = const.

345

III. Кривые и поверхности второго порядка

	y2			= −2z +			x	2
								0		(22.26)
	b2						a2
è y = y0 = const :
		x2		= 2z −		y2
						0				(22.27)
		a2			b2

являются параболами с тем же параметром, что и первые две параболы, но с другими вершинами. Например, вершины парабол (22.26), направленных вниз, лежат на параболе (22.24), а вершины парабол (22.27), направленных вверх, лежат на параболе (22.25).

Пересечения параболоида с любой горизонтальной плоскостью являются гиперболами. Причем в области положительных значений z эти гиперболы являются прямыми гиперболами, а в области отрицательных — сопряженными:

x2

−

y2

= 2z,

z = z

x2

−

y2

= 2z

.

(22.28)

a2

b2

0

a2

b2

0

Ðèñ. 22.4. Гиперболический параболоид

На рис. 22.4 гиперболический параболоид нарисован двумя различными способами. Эти способы отличаются линиями, которые

346

22. Поверхности второго порядка

выбраны в качестве границ изображенной части поверхности. Так, на рис. 22.4 а) границами являются параболы (22.26) и гиперболы (22.28) для отрицательных значений z0 . На рис. 22.4 б) роль границ играют параболы, направленные вверх (22.27), и гиперболы (22.28) для отрицательных значений z0.

На плоскости z = 0 сопряженные гиперболы (22.28) вырождаются в пару пересекающихся прямых кривых:

	x2	−	y2	= 2z, z = 0	x2	−	y2	= 0.	(22.29)
	a2		b2		a2		b2

Причем эти прямые полностью содержатся в параболоиде. Этот факт, на первый взгляд, является неожиданным. Ведь гиперболический параболоид, все-таки достаточно далекая от плоскости поверхность. Но оказывается, эти прямые не единственные, которые содержит параболоид. Более того, весь параболоид можно представить себе полностью составленным из прямых. То есть, гиперболический параболоид является линейчатой поверхностью (см. раздел 14).

Чтобы это показать, достаточно заметить, что в уравнение гиперболического параболоида входит квадрат разности координат, который можно представить в виде произведения соответствующих суммы и разности:

x2

y2

x

y x

y

= 2z.

−

=

−

+

(22.30)

a

2

b

2

a

b a

b

Теперь одну из этих скобок можно приравнять к какому-ни- будь числу, например, ax − by = t, и мы получим систему двух уравнений первой степени:

		x		−	y	= t
		a			b		.	(22.31)
	x				y
t			+t				= 2z
					b
a

347

III. Кривые и поверхности второго порядка

Каждое из этих уравнений представляет собой плоскость, а, следовательно, система (22.31) описывает некоторую прямую. Величина t играет роль параметра, разные значения которого соответствуют различным прямым. Таким образом, при непрерывном изменении параметра t от −∞ до +∞ мы получим множество прямых, полностью покрывающих гиперболический параболоид.

Задача 22.1. Покажите, что эллипсоид можно получить, сжимая в одном из направлений эллипсоид вращения — фигуру вращения полученную из эллипса.

Задача 22.2. Покажите, что однополостный гиперболоид является линейчатой поверхностью.

Задача 22.3. Предложите практический способ, позволяющий определить положение фокуса круговой параболической антенны.

348

22.Поверхности второго порядка

22.6.Краткие сведения

оповерхностях второго порядка

349

III. Кривые и поверхности второго порядка

ЛИТЕРАТУРА

1.Моденов П. С. Аналитическая геометрия. — М:. Изд-во Московского университета, 1969 г.

2.Александров П.П. Лекции по аналитической геометрии. — М:. Наука, 1968 г.

3.Постников М. М. Аналитическая геометрия. — М:. Наука. 1973 г.

4.Ильин В. А., Поздняк Э. Г. Аналитическая геометрия. — М:. Главная редакция ôèç.-ìàò. ëèò., 1981 ã.

5.Моденов П. С., Пархоменко А. С. Сборник задач по аналити- ческой геометрии. — М:. Главная редакция ôèç.-ìàò. ëèò., 1976 ã.

6.Ефимов Н. В. Краткий курс аналитической геометрии. М:. Высшая школа, 1998.

7.Беклемишев Д. В. Курс аналитической геометрии и линейной алгебры. — М:. Высшая школа, 1998.

8. Резниченко С. В. Аналитическая геометрия в примерах

èзадачах. — М:. Èçä-âë ÌÔÒÈ, 2001.

9.Роджерс Д. Алгоритмические основы машинной графики. — М:. Мир, 1989.