Учебник

14. Кривые и поверхности в аналитической геометрии

На этих двух примерах мы убедились, что если кривая задана в одной системе отсчета полиномом определенного порядка, то в другой системе отсчета она также описывается полиномом, причем такого же порядка. Оказывается, это утверждение является достаточно общим и его можно доказать для произвольных линейных преобразований координат. Напомним, что поворот и параллельный перенос систем координат приводит к линейной связи между старыми и новыми координатами.

Для того чтобы доказать неизменность порядка полинома, введем понятие алгебраических кривых как кривых, уравнения которых имеют вид полинома определенного порядка.

Определение алгебраических кривых

Алгебраическая кривая порядка N — это кривая, уравнение которой имеет вид полинома N -го порядка:

i+ j≤N

∑ aij xi y j = 0. i, j=0

Напомним, что порядком полинома называется максимальная суммарная степень у переменных, входящих в одно слагаемое

aij xi y j .

N = max(i + j).

Например, полином x3 + 2xy − y = 0 имеет третий порядок,

àпорядок полинома x3 + 2x2 y2 − y = 0 равен четырем. Теперь мы можем доказать следующую теорему.

Теорема об инвариантности порядка алгебраической кривой

При линейных преобразованиях координат порядок алгебраической кривой не изменяется.

Доказательство

1. Предположим, что нам задана кривая N -го порядка уравнением:

223

II.Прямые и плоскости. Кривые и поверхности

i+ j≤N

∑aij xi y j = 0

i, j=0

и мы совершаем линейное преобразование координат по закону

x = Ax′ + By′+C

y = Dx′ + Ey′+ F .

Тогда в новых координатах уравнение кривой будет выглядеть так:

i+ j≤N

∑ aij (Ax′ + By′ +C)i (Dx′+ Ey′+ F)j = 0.

i, j=0

Из всех слагаемых в этой сумме выберем то, у которого сумма показателей максимальна и равна, по определению, порядку полинома. Пусть, например, это будет слагаемое, содержащее обе переменные:

aij xi y j = aij (Ax′ + By′+C)i (Dx′+ Ey′+ F)j ,

ãäå i + j = N.

Возведем трехчлены, стоящие в скобках, в соответствующие степени

(Ax′+ By′+C )i = (Ax′)i +(By′)i +... è

(Dx′ + Ey′ + F)j = (Dx′)j +(Ey′)j +...,

оставив только слагаемые с максимальными показателями. После перемножения этих выражений мы получим многочлен:

(Ax′ + By′ +C)i (Dx′+ Ey′+ F)j = ((Ax′)i +(By′)i ) ((Dx′)j +(Ey′)j )+... =

= (Ax′)i (Dx′)j +(By′)i (Dx′)j +(Ax′)i (Ey′)j +(By′)i (Ey′)j +... =...

Мы видим, что результат произведения содержит одночлены порядка N, например, (Ax′)i (Dx′)j . Следовательно, в новой системе отсчета порядок исходного полинома не изменится. ■

224

14. Кривые и поверхности в аналитической геометрии

Следует отметить, что существуют такие линейные преобразования, при которых, после перехода в новую систему отсчета старшие члены взаимно сокращаются и полином оказывается меньшего порядка, чем в исходной системе. В нашем курсе мы ограничиваемся только исследованиями таких преобразований, при которых такого сокращения не происходит. Исследование преобразований, уменьшающих степень полиномов, выходит за рамки нашего курса.

Напомним, что мы уже применяли эту теорему при выводе общего уравнения прямых и плоскостей и будем ее использовать при исследовании кривой второго порядка.

14.3. Поверхности, составленные из прямых. Цилиндр

Мы увидели, что поверхности можно описывать уравнением f (x, y, z) = 0. Однако такой вид уравнения настолько общий, что он, казалось бы, не позволяет сделать никаких выводов о свойствах самой кривой. Однако это не так.

Давайте предположим, что функция f (x, y, z) является функцией только одной переменной, например f = f (x). Тогда поверхность с уравнением f (x) = 0 будет состоять из плоскостей, параллельных плоскости YOZ.

Убедиться в этом можно после таких рассуждений. Пусть вели-

÷èíà	x0	является корнем уравнения	f (x) = 0, òî åñòü	f (x0 ) = 0,
Тогда	координаты точки M (x0 ,0,0)		удовлетворяют	уравнению
f (x) = 0		и, следовательно, точка M (x0 ,0,0) принадлежит данной

поверхности. Но, так как уравнение этой поверхности не зависит ни от y, íè îò z, то и координаты любой точки N(x0 , y, z) (абсцисса которой совпадает с абсциссой точки M (x0 ,0,0)) также удовлетворяют уравнению поверхности, а значит, принадлежат ей. Следовательно, все точки пространства с одинаковой абсциссой, а это множество точек является плоскостью, параллельной YOZ, принадлежат данной поверхности.

Рассуждать можно и по-другому. Если	x0 является корнем
уравнения поверхности, то есть f (x 0 ) = 0,	то уравнение поверх-

225

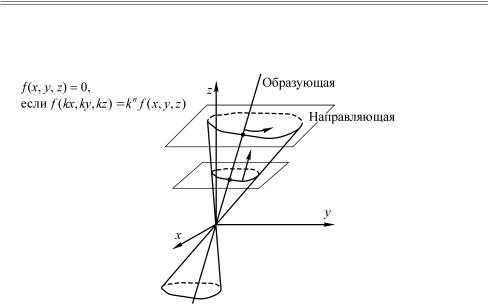
II. Прямые и плоскости. Кривые и поверхности

ности f (x) = 0 можно представить в виде x = x 0. А это ни что иное, как уравнение плоскости, параллельной YOZ.

Главной особенностью этих рассуждений является то, что нам не потребовался явный вид функции f (x).

Теперь предположим, что функция f (x, y, z) является функцией только двух переменных, например, f = f (x, y). Тогда, поверхность с уравнением f (x, y) = 0 будет состоять из прямых параллельных оси OZ.

Убедиться в этом можно двумя способами.

1. Предположим, что нам известна точка M (x0 , y0 , zM ), координаты которой удовлетворяют уравнению поверхности: f (x, y) = 0. Возьмем другую точку N(x0 , y0 , zN ), которая отличается от точки M (x0 , y0 , zM ) только третьей координатой z. Так как уравнение поверхности не зависит от координаты z , то после подстановки координат точки N(x0 , y0 , zN ) в уравнение поверхности мы получим то же самое значение функции f , что и для точки M : f (xN , yN ) = f (x0 , y0 ). А это выражение, в силу того, что точ- ка M принадлежит поверхности, равно нулю. Следовательно, и координаты точки N(x0 , y0 , zN ) удовлетворяют уравнению данной поверхности, а значит, и сама точка N принадлежит этой поверхности. Вместе с ней этой поверхности принадлежат все точки, отличающиеся от точки M только координатой z, а это множество точек является прямой, параллельной оси Z.

2. Допустим, мы нашли корни x0 , y0 уравнения f (x, y) = 0, òî åñòü f (x0 , y0 ) = 0. Тогда этой поверхности будут принадлежать âñå точки с координатами, удовлетворяющими следующим условиям:

x = x0 .y = y0

А эта система представляет собой уравнение прямой в пространстве как пересечения двух плоскостей, причем эта прямая параллельна оси Z.

Таким образом, поверхность, заданная уравнением
f (x, y) = 0,	(14.18)

226

14. Кривые и поверхности в аналитической геометрии

полностью состоит из прямых, параллельных между собой. Такие поверхности принято называть цилиндрами. Параллельные прямые, которые, собственно, и образуют цилиндр, называют образующими.

Цилиндр — это поверхность, образованная параллельными прямыми. Уравнение цилиндра можно записать в виде уравнения f (x, y) = 0, в котором отсутствует одна из координат.

Второе утверждение можно доказать из первого. Попробуйте сделать это самостоятельно, выбрав такую систему отсчета, в которой ось аппликат параллельна образующим.

Ðèñ. 14.2. Цилиндр и уравнение цилиндра. Стрелками показаны движения образующих или направляющих,

приводящие к построению цилиндра

Исследовать форму этой поверхности можно и таким способом. Давайте рассмотрим плоскость XOY. Тогда уравнение f (x, y) = 0 представляет собой уравнение некоторой кривой в плоскости XOY. Строго говоря, эта кривая является пересечением поверхности f (x, y) = 0 и плоскости z = 0, а значит, описывается системой уравнений:

227

II.Прямые и плоскости. Кривые и поверхности

f (x, y) = 0

z = 0 .

Через эту кривую проходят все образующие, и можно считать, что цилиндр получается движением одной из образующих вдоль этой кривой. Поэтому такая кривая называется направляющей. Под этим названием имеется в виду, что если мы двигаем одну из образующих так, чтобы она оставалась параллельной самой себе и при этом имела всегда только одну точку пересечения с направляющей, то тогда образующая «заметает» поверхность, которую называют цилиндром.

Пересечение цилиндра с другими горизонтальными плоскостями z = z0 дается системой

f (x, y) = 0	,
z = z0

а значит, дает такую же связь между координатами x, y, как и в плоскости XOY. Таким образом, можно считать, что цилиндр образован при движении направляющей вдоль оси OZ.

В завершение раздела отметим, что направляющая не обязательно должна быть перпендикулярна образующим, и более того, она может и не лежать в одной плоскости. То есть, в общем слу- чае уравнение направляющей выглядит как

f (x, y) = 0g(x, y, z) = 0 ,

ãäå g(x, y, z) = 0 — уравнение произвольной поверхности. Необходимо лишь, чтобы направляющая имела общие точки со всеми образующими.

14.4. Поверхности, составленные из прямых. Конусы

Цилиндр является не единственной поверхностью, которую можно получить движением прямой. Такие поверхности называются линейчатыми, и ниже мы рассмотрим еще несколько примеров таких поверхностей.

228

14. Кривые и поверхности в аналитической геометрии

Для того чтобы рассмотреть еще один частный случай поверхностей, заданных уравнением f (x, y) = 0, вернемся к двумерной системе координат и рассмотрим уравнение прямой, проходящей через начало отсчета, например, y = kx. Эта прямая обладает своеобразным свойством подобия. Если взять две точки, абсциссы которых отличаются, например, в три раза, то и ординаты у этих точек также будут отличаться в три раза. То есть, для

любого числа N

	y = kx Ny = kNx.
Этим свойством	íå	обладают многие функции, например,
y = kx +b èëè y =	x,	потому что Ny ≠ kNx +b è Ny ≠ Nx. Îä-

нако, существует целый ряд функций, для которых это правило выполняется, например, y2 = a2 x2 , y4 −a2 y2 x2 +bx4 = 0 и тому подобных. Такие функции выделяют в особый класс однородных функций, которые определяют следующим образом. Однородными называются функции f (x, y), для которых для любого числа

k справедливо следующее соотношение:
	f (kx, ky) = kn f (x, y).
Число n называется показателем однородности функ-
ции. Например,	показатель однородности функции f (x, y) =
= y4 −a2 y2 x2 +bx4	равен четырем.

Грубо говоря, однородные функции допускают масштабирова-
ние координат. То есть графики кривых, заданных уравнением
f (x, y) = 0,	когда f (x, y) — однородная функция, переходит сам
â ñåáÿ ïðè	увеличении координат в одинаковое число раз, и, ес-

тественно, проходит через начало координат.

Посмотрим, как выглядит график какой-нибудь однород-

ной функции f (x, y) = 0 íà	плоскости. Предположим, что точ-
êà (x0 , y0 ) принадлежит	этой кривой, то	åñòü f (x0 , y0 ) = 0.
Тогда можно показать,	что любая точка	ñ	координатами
(x, y) = (kx0 , ky0 ), при произвольном значении k			также принад-
лежит этой кривой:

229

II. Прямые и плоскости. Кривые и поверхности

f (x, y) = f (kx , ky ) = kn f (x , y ) = kn 0				f (x, y) = 0.
0	0	0	0

Но координаты точки (x, y) связаны между собой соотноше-

íèåì y / y0 = x / x0 .

Это соотношение есть не что иное, как уравнение прямой. Следовательно, кривые, заданные уравнением f (x, y) = 0, ãäå f (x, y) — однородная функция, являются прямыми, проходящими через начало отсчета.

Вернемся к трехмерному пространству и рассмотрим поверхности, уравнение которых выражается через однородные функции:

f (x, y, z) = 0, åñëè f (kx, ky, kz) = kn f (x, y, z).

(14.19)

Повторяя те же самые рассуждения, что и для плоскости, мы получаем, что координаты точек на этой поверхности связаны между собой соотношением

	y	=	x	=	z		,	(14.20)
	y		x		z	0
	0		0

где точка (x0 , y0 , z0 ) — одна из точек на поверхности. А это соотношение является уравнением прямой, проходящей через начало отсчета. Таким образом, если некоторая точка (x0 , y0 , z0 ) принадлежит поверхности (14.19), то вместе с ней этой поверхности принадлежит и вся прямая (14.20), проходящая через на- чало координат и эту точку. Значит, эта поверхность полностью состоит из прямых, проходящих через начало координат. Такие поверхности называются конусами.

Конус — это поверхность, образованная прямыми, проходящими через одну точку — вершину конуса. Уравнение конуса можно записать в виде f (x, y, z) = 0, ãäå f (x, y, z) — однородная функция.

Мы только что доказали, что уравнение (14.19) описывает конус согласно его определению. Однако, для согласованности такого определения еще нужно доказать, что уравнение любого конуса как множества кривых может быть выражено через какую-то однород-

230

14. Кривые и поверхности в аналитической геометрии

ную функцию. Попробуйте сделать это самостоятельно, выбрав такую систему отсчета, центр которой совпадает с вершиной конуса.

Ðèñ. 14.3. Конус и уравнение конуса. Стрелками показаны движения образующих

или направляющих, приводящие к построению конуса

Прямые, из которых состоит конус, называются образующими. Давайте в пространстве проведем плоскость с уравнением A1x + B1 y +C1z + D1 = 0, не проходящую через вершину конуса и пересекающую âñå образующие конуса. Линия пересечения конуса и этой плоскости будет описываться системой уравнений

f (x, y, z) = 0

A1x + B1 y +C1z + D1 = 0

и пересекать все образующие конуса. Эта кривая, как и в цилиндре, называется направляющей. Это значит, что если мы возьмем любую образующую, проходящую через вершину конуса, и будем двигать ее так, чтобы она имела всегда только одну точку пересечения с направляющей, то тогда образующая «заметет» собой всю поверхность конуса.

Àтеперь возьмем каждую из точек направляющей и умножим

ååкоординаты на одно и то же число:

231

II. Прямые и плоскости. Кривые и поверхности

(x, y, z) → (x′, y′, z′) = k(x, y, z).

Мы получим координаты точек новой кривой, которая является пересечением конуса с поверхностью, уравнение которой получается из уравнения исходной плоскости:

A1x + B1 y +C1z + D1 = 0 → A1 xk′ + B1 yk′ +C1 zk′ + D1 =

=0 → A1x′+ B1 y′+C1z′+ D1k = 0.

Àэто, — уравнение плоскости параллельной исходной. Значит, конус может быть получен плоскопараллельным дви-

жением направляющей с постепенным ее масштабированием.

Ðèñ. 14.4. Однополостный гиперболоид (а) и гиперболический параболоид (б) как линейчатые поверхности.

Приведены примеры прямолинейных образующих

Наряду с только что рассмотренными поверхностями — цилиндрами и конусами — существуют и простейшие линейчатые поверхности. Это плоскости, которые одновременно являются и цилиндрами, и конусами.

232