
- •Определение вероятности.
- •Теоремы сложения и умножения вероятностей.
- •Формула полной вероятности и формула Байеса.
- •Формулы Бернулли и Пуассона.
- •Закон распределения вероятностей.
- •6. Математическое ожидание и дисперсия.
- •7. Функция распределения и плотность вероятности.
- •8. Равномерное распределение.
- •9. Эмпирическая функция распределения.
- •Определения
- •13.Проверка нулевой гипотезы.
-
Формулы Бернулли и Пуассона.
Формула Бернулли удобна для вычислений лишь при сравнительно небольшом числе испытаний n. При больших значениях n пользоваться этой формулой неудобно. Чаще всего в этих случаях используют формулу Пуассона. Эта формула определяется теоремой Пуассона.
Теорема.
Если вероятность p наступления события
A в каждом испытании постоянна и мала,
а число независимых испытаний n достаточно
велико, то вероятность наступления
события A ровно m раз приближенно равна
Pn(m)
= ![]()
![]()
![]()
![]() ,
где
,
где ![]()
![]() .
.
Доказательство.
Пусть даны вероятность наступления
события A в одном испытании p и число
независимых испытаний n. Обозначим ![]()
![]() .
Откуда p =
.
Откуда p = ![]()
![]() .
Подставим это выражение в формулу
Бернулли:
.
Подставим это выражение в формулу
Бернулли:
Pn(m)
= ![]()
![]() (
(![]()
![]() )m(1
–
)m(1
– ![]()
![]() )n-m
=
)n-m
=
![]()
![]() m\
nm
m\
nm
![]()
![]() (1
-
(1
-![]()
![]() )n(1
–
)n(1
– ![]()
![]() )-m
=
)-m
= ![]()
![]() m\m!
* (n - 1)\ n * (n - 2)\n * (n – m +1)\n * (1 –
m\m!
* (n - 1)\ n * (n - 2)\n * (n – m +1)\n * (1 – ![]()
![]() )n
(1 –
)n
(1 – ![]()
![]() )-m
=
)-m
= ![]()
![]() m\
m! (1 –1\n) (1 – 2\n) … (1 – (m-1)\n) (1 –
m\
m! (1 –1\n) (1 – 2\n) … (1 – (m-1)\n) (1 – ![]()
![]() )n
(1
–
)n
(1
– ![]()
![]() )-m.
)-m.
При достаточно большом !!n,, и сравнительно небольшом !!m,, все скобки, за исключением предпоследней, можно принять равными единице, т.е.
Pn(m)
= ![]()
![]() m\
m! (1 –
m\
m! (1 – ![]()
![]() )n.
)n.
Учитывая
то, что n достаточно велико, правую часть
этого выражения можно рассмотреть при
n ![]()
![]() ,
т.е. найти предел
,
т.е. найти предел ![]()
![]() n
=
n
=
![]()
![]() .
.
Тогда
получим Pn(m)
= ![]()
![]() m\m!
*
m\m!
* ![]()
![]() .
.
-
Закон распределения вероятностей.
Распределение вероятностей — это закон, описывающий область значений случайной величины и вероятности их принятия.
Определение.
Пусть задано вероятностное пространство
(![]()
![]() ),
и на нём определена случайная величина
X :
),
и на нём определена случайная величина
X : ![]()
![]() .
В частности, по определению, X является
измеримым отображением измеримого
пространства (
.
В частности, по определению, X является
измеримым отображением измеримого
пространства (![]()
![]() )
в измеримое пространство (R,
)
в измеримое пространство (R, ![]()
![]() ),
где
),
где ![]()
![]() обозначает борелевскую сигма-алгебру
на R. Тогда случайная величина X индуцирует
вероятностную меру Px
на R следующим образом:
обозначает борелевскую сигма-алгебру
на R. Тогда случайная величина X индуцирует
вероятностную меру Px
на R следующим образом:
Px(B)
= P(X-1(B)),
![]()
![]() .
.
Мера
Px
называется распределением случайной
величины X. Иными словами, Px(B)
= P(X![]()
![]() ),
таким образом Px(B)
задаёт вероятность того, что случайная
величина попадает во множество B
),
таким образом Px(B)
задаёт вероятность того, что случайная
величина попадает во множество B![]()
![]() .
.
6. Математическое ожидание и дисперсия.
Математическое ожидание - число, вокруг которого сосредоточены значения случайной величины. Математическое ожидание случайной величины x обозначается Mx .
Математическое ожидание дискретной случайной величины x , имеющей распределение
|
x1 |
x2 |
... |
xn |
|
p1 |
p2 |
... |
pn |
называется
величина ![]() ,
если число значений случайной величины
конечно.
,
если число значений случайной величины
конечно.
Если
число значений случайной величины
счетно, то ![]() .
При этом, если ряд в правой части равенства
расходится, то говорят, что случайная
величина x не имеет математического
ожидания.
.
При этом, если ряд в правой части равенства
расходится, то говорят, что случайная
величина x не имеет математического
ожидания.
Математическое
ожидание непрерывной случайной величины
с плотностью вероятностей px
(x)
вычисляется по формуле 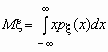 .
При этом, если интеграл в правой части
равенства расходится, то говорят, что
случайная величина x не имеет математического
ожидания.
.
При этом, если интеграл в правой части
равенства расходится, то говорят, что
случайная величина x не имеет математического
ожидания.
Если случайная величина h является функцией случайной величины x , h = f(x), то
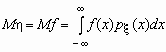 .
.
Аналогичные формулы справедливы для функций дискретной случайной величины:
![]() ,
,
![]() .
.
Основные свойства математического ожидания:
-
математическое ожидание константы равно этой константе, Mc=c ;
-
математическое ожидание - линейный функционал на пространстве случайных величин, т.е. для любых двух случайных величин x , h и произвольных постоянных a и b справедливо: M(ax + bh ) = a M(x )+ b M(h );
-
математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(x h ) = M(x )M(h ).
Дисперсия случайной величины характеризует меру разброса случайной величины около ее математического ожидания.
Если случайная величина x имеет математическое ожидание Mx , то дисперсией случайной величины x называется величина Dx = M(x - Mx )2.
Легко показать, что Dx = M(x - Mx )2= Mx 2 - M(x )2.
Эта универсальная формула одинаково хорошо применима как для дискретных случайных величин, так и для непрерывных. Величина Mx 2 >для дискретных и непрерывных случайных величин соответственно вычисляется по формулам
![]() ,
,
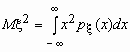 .
.
Для
определения меры разброса значений
случайной величины часто используется
среднеквадратичное
отклонение ![]() ,
связанное
с дисперсией соотношением
,
связанное
с дисперсией соотношением ![]() .
.
Основные свойства дисперсии:
-
дисперсия любой случайной величины неотрицательна, Dx
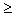 0;
0;
-
дисперсия константы равна нулю, Dc=0;
-
для произвольной константы D(cx ) = c2D(x );
-
дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D(x ± h ) = D(x ) + D (h ).
