8. Равномерное распределение.

Непрерывная случайная величина x , принимающая значения на отрезке [a, b], распределена равномерно на [a, b], если ее плотность распределения p_x (x) и функция распределения F_x (x ) имеют соответственно вид:

, .

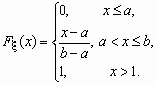
На практике встречаются случайные величины, о которых заранее известно, что они могут принять какое-либо значение в строго определенных границах, причем в этих границах все значения случайной величины имеют одинаковую вероятность (обладают одной и той же плотностью вероятностей).

Например, при поломке часов остановившаяся минутная стрелка будет с одинаковой вероятностью (плотностью вероятности) показывать время, прошедшее от начала данного часа до поломки часов. Это время является случайной величиной, принимающей с одинаковой плотностью вероят­ности значения, которые не выходят за границы, определенные продолжительностью одного часа. К подобным случайным величинам относится также и погрешность округления. Про такие величины говорят, что они распределены равномерно, т. е. имеют равномерное распределение.

Определение. Непрерывная случайная величина Х имеет равномерное распределение на отрезке [а, в], если на этом отрезке плотность распределения вероятности случайной величины постоянна, т. е. если дифференциальная функция распределения f(х) имеет следующий вид:

Иногда это распределение называют законом равномерной плотности. Про величину, которая имеет равномерное распределение на некотором отрезке, будем говорить, что она распределена равномерно на этом отрезке.

Найдем значение постоянной с. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то

откуда с=1/(b-a).

Теперь функцию f(x) можно представить в виде

 

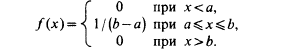
Построим функцию распределения F(x), для чего найдем выражение F(x) на интервале [a, b]:

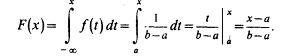
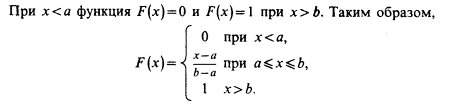
Графики функций f(x) и F(x) имеют вид:

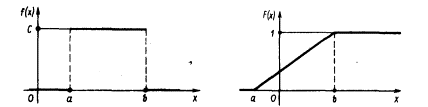
Найдем числовые характеристики.

Используя формулу для вычисления математического ожидания НСВ, имеем:

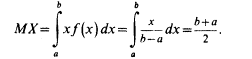
Таким образом, математическое ожидание случайной вели­чины, равномерно распределенной на отрезке [a, b] совпадает с серединой этого отрезка.

Найдем дисперсию равномерно распределенной случайной величины:

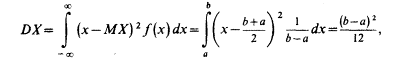
откуда сразу же следует, что среднее квадратическое отклонение:

Найдем теперь вероятность попадания значения случайной величины, имеющей равномерное распределение, на интервал (,), принадлежащий целиком отрезку [a, b]:

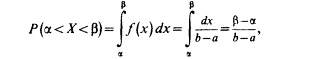
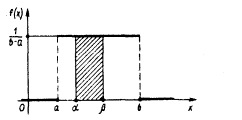
Геометрически эта вероятность представляет собой площадь заштрихованного прямоугольника. Числа а и b называются параметрами распределения и однозначно определяют равномерное распределение.

9. Эмпирическая функция распределения.

Эмпирическая функция распределения (выборочная функция распределения) — естественное приближение теоретической функции распределения данной случайной величины, построенное по выборке.

Определения

Пусть задана случайная выборка наблюдений Построим по выборке ступенчатую функцию , возрастающую скачками величины в точках Построенная функция называется эмпирической функцией распределения. Для задания значений в точках разрыва формально определим её так:

Замечание: при этом эмпирическая функция непрерывна справа.

На рисунке представлена функция стандартного нормального распределения и эмпирическая функция распределения, построенная по выборке из 10 случайных наблюдений из стандартного нормального закона.

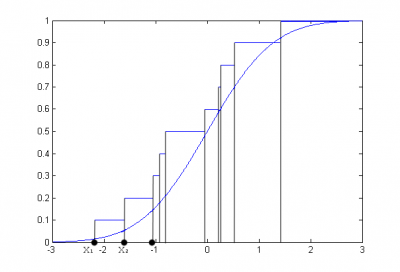
Пример эмпирической функции распределения, построенной по выборке из 10 наблюдений.

Свойства эмпирической функции распределения

Эмпирическое распределение для фиксированного

Поскольку случайная величина имеет распределение Бернулли с вероятностью успеха (где - теоретическая функция распределения случайной величины ), а последовательность - схема Бернулли с вероятностью успеха , то по отношению к этой последовательности есть частота попаданий левее x.

Из сказанного вытекает, что эмпирическое распределение служит естественным приближением к теоретической функции распределения.

Математическое ожидание и дисперсия эмпирического распределения

Математическое ожидание эмпирической функции распределения

• 

таким образом эмпирическое распределение является несмещённой оценкой теоретической функции распределения .

Дисперсия эмпирического распределения

• 

Асимптотические свойства эмпирической функции распределения

1. По усиленному закону больших чисел сходится почти наверное к теоретической функции распределения :

почти наверное при

2. Выборочная функция распределения является асимптотически нормальной оценкой функции распределения при условии, что :

при

10.Полигон и гистограмма.

Полигоном частот называют ломаную линию, отрезки которой соединяют точки . Для построения полигона частот на оси абсцисс откладывают варианты , а на оси ординат – соответствующие им частоты и соединяют точки отрезками прямых.

Полигон относительных частот строится аналогично, за исключением того, что на оси ординат откладываются относительные частоты .

В случае непрерывного признака строится гистограмма, для чего интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала – сумму частот вариант, попавших в i–й интервал.

Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которой служат частичные интервалы длиною h, а высоты равны отношению . Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии (высоте) . Площадь i–го прямоугольника равна – сумме частот вариант i–о интервала, поэтому площадь гистограммы частот равна сумме всех частот, т.е. объему выборки.

В случае гистограммы относительных частот по оси ординат откладываются относительные частоты , на оси абсцисс – частичные интервалы, над ними проводят отрезки, параллельные оси абсцисс на высоте . Площадь i–го прямоугольника равна относительной частоте вариант , попавших в i–й интервал. Поэтому площадь гистограммы относительных частот равна сумме всех относительных частот, то есть единице.

11.Выборочная средняя.

Пусть для изучения генеральной совокупности относительно количественного признака Х извлечена выборка объема n.

  Выборочной средней называют среднее арифметическое значение признака выборочной совокупности.

Если все значения признака выборки различны, то

если же все значения имеют частоты n₁, n₂,…,n_k, то

Выборочная средняя является несмещенной и состоятельной оценкой генеральной средней.

Замечание: Если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

12.Доверительный интервал.

Доверительный интервал — термин, используемый в математической статистике при интервальной (в отличие от точечной) оценке статистических параметров, что предпочтительнее при небольшом объёме выборки. Доверительным называют интервал, который покрывает неизвестный параметр с заданной надёжностью.

Метод доверительных интервалов разработал американский статистик Ю. Нейман, исходя из идей английского статистика Р. Фишера.

Доверительным интервалом параметра θ распределения случайной величины X с уровнем доверия 100p%, порождённым выборкой (x₁,…,x_n), называется интервал с границами (x₁,…,x_n) и (x₁,…,x_n), которые являются реализациями случайных величин L(X₁,…,X_n) и U(X₁,…,X_n), таких, что

.

Граничные точки доверительного интервала и называются доверительными пределами.

Интерпретация доверительного интервала, основанная на интуиции, будет следующей: если p велико (скажем, 0,95 или 0,99), то доверительный интервал почти наверняка содержит истинное значение θ.

Еще одно истолкование понятию доверительного интервала: его можно рассматривать как интервал значений параметра θ, совместимых с опытными данными и не противоречащих им.