
- •Н. Н. Пустовалова компьютерные информационные технологии лабораторный практикум
- •Лабораторная работа № 1. Операционная система Windows. Программы группы «Стандартные»
- •Лабораторная работа № 2. Приложение Microsoft Word Задание 1
- •Задание 2
- •Программирование циклических процессов
- •Лабораторная работа № 3. Приложение Microsoft Excel Задание 1
- •Зарплата работников за январь
- •Задание 2
- •Лабораторная работа № 4. Реализация алгоритмов линейной структуры в приложении Excel Задание 1
- •Задание 2
- •Лабораторная работа № 5. Циклы в инженерных расчетах
- •Лабораторная работа № 6. Разветвляющиеся программы в приложении Excel
- •Лабораторная работа № 7. Одномерные массивы
- •Лабораторная работа № 8. Использование подпрограмм
- •Лабораторная работа № 9. Создание форм пользователя в приложении Excel
- •Лабораторная работа № 10. Простые и комбинированные списки
- •Лабораторная работа № 11. Разработка проекта с использованием форм в приложении Excel Задание 1
- •Задание 2
- •Лабораторная работа № 12. Создание баз данных в приложении Access Задание 1
- •Задание 2
- •Задание 3
- •Лабораторная работа № 13. Разработка презентации в PowerPoint
- •Задание 3
- •Лабораторная работа № 15. Графический редактор Adobe Photoshop Задание 1
- •Задание 2
- •Лабораторная работа № 16. Приложение Machcad Задание 1
- •Лабораторная работа № 17. Приближенное вычисление интегралов
- •Лабораторная работа № 18. Приближенное решение уравнений
- •Лабораторная работа № 19. Решение систем уравнений в приложениях Excel и Machcad
- •Лабораторная работа № 20. Математические модели одномерных процессов
- •Лабораторная работа № 21. Оптимизация процессов
- •Лабораторная работа № 22. Решение дифференциальных уравнений
- •Лабораторная работа № 23. Компьютерная графика. Приложение Macromedia Flash Задание 1
- •Задание 2
- •Лабораторная работа № 24. Создание html-документов в сети Интернет
- •Операционная система windows
- •Программы группы «стандартные»
- •Приложение microsoft word
- •Приложение microsoft excel
- •Линейные программы в приложении excel
- •Циклические программы
- •Разветвляющиеся программы
- •Одномерные массивы
- •Использование подпрограмм
- •Формы пользователя
- •Работа со списками
- •Использование мастера слияния
- •Базы данных
- •Создание таблиц
- •Заполнение, сохранение и редактирование данных в таблице. Порядок заполнения таблиц зависит от связей в таблицах. Вначале заполняются таблицы главные, затем – подчиненные.
- •Итоговый запрос. Чтобы подводить итоговые значения по группам данных, используются итоговые запросы. Например, пусть надо получить итоговые суммы по продажам отдельных групп товаров.
- •Создание форм
- •Разработка отчетов
- •Приложение power point
- •Компьютерная графика. Приложение ms visio
- •Выделение областей. Для выделения всего рисунка или слоя служит команда Select / All (Выделение / Все).
- •Приложение mathcad
- •Вычисление определенных интегралов
- •Согласно методу трапеций значение интеграла определяется по формуле
- •Приближенное решение уравнений
- •Решение систем линейных уравнений
- •Рассмотрим алгоритм решения системы линейных уравнений методом Гаусса.
- •Получение математической модели одномерного объекта
- •Решение задач оптимизации
- •Приближенное решение дифференциальных уравнений
- •Приложение macromedia flash
- •Создание html-документов
- •Компьютерные информационные технологии
Приближенное решение дифференциальных уравнений
Рассмотрим дифференциальное уравнение первого порядка:
![]()
Требуется найти решение на интервале [x0, xn], удовлетворяющее начальному условию y(x0) = y0.
Для приближенного решения дифференциального уравнения интервал [x0, xn] разбивается на n частей с шагом h:
xi+1 = xi + h, i = 0, 1, 2, …, n – 1.
Согласно методу Эйлера значения yi определяются по формуле
yi+1 = yi + h f(xi, yi).
Алгоритм метода Эйлера.
1. Ввод n, конечного значения xn, начального значения x0 (в переменную x), ввод y0 (в переменную y).
2.
Вычисление h
=![]() x
= x0,
y
= y0.
x
= x0,
y
= y0.
3. Вывод x, y.
4. Вычисление y = y + hf(x,y), x = x + h.
5. Если x > xn, то переход к пункту 6, иначе – переход к пункту 3.
6. Конец вычислений.
Например, пусть нужно найти решение дифференциального уравнения на отрезке [0, 1].
![]()
Зная начальные условия, определим y(0,01) и y(0,02):
y(0,01) = 1 + 0,01( – 21 + 0) = – 0,98;
y(0,02) = – 0,98 + 0,01( – 2( – 0,98) + 0,01) = –0,78.
Аналогичным образом определяются остальные значения y на отрезке [0, 1].
Для получения достоверных результатов значение h должно быть достаточно мало, при этом можно не выводить все получающиеся значения x и y. Целесообразно внести изменения в алгоритм программы так, чтобы вычисления проводились с малым шагом, а вывод результатов − с большим.
Расчетные формулы метода Рунге – Кутта четвертого порядка имеют вид:
k1 = hf(xi, yi),
k2
=
hf(xi
+
![]() ,
yi
+
,
yi
+
![]() ),
),
k3
=
hf(xi
+
![]() ,
yi
+
,
yi
+
![]() ),
),
k4 = hf(xi + h, yi + k3),
yi+1
= yi
+
![]() (k1
+ 2 k2
+ 2 k3
+ k4),
xi+1
= xi
+ h,
i
= 0, 1, 2, …, n
– 1.
(k1
+ 2 k2
+ 2 k3
+ k4),
xi+1
= xi
+ h,
i
= 0, 1, 2, …, n
– 1.
Для разработки программы, реализующей метод Рунге – Кутта можно использовать тот же алгоритм, что и для метода Эйлера, внеся в него соответствующие изменения.
Решение дифференциальных уравнений в приложении Excel. Пусть имеется дифференциальное уравнение
![]() x0
= 0, y0
= 1, h
=
0,1.
x0
= 0, y0
= 1, h
=
0,1.
Надо найти решение на отрезке [0; 1].
Программа решения этого уравнения методом Эйлера может иметь следующий вид:
Sub CommandButton1_Click()
х = Val(InputBox(“Введите начальное значение х”))
y = Val(InputBox(“Введите начальное значение y”))
хn = Val(InputBox(“Введите конечное значение х”))
h = Val(InputBox(“Введите шаг”))
i = 1
Do
y = y + h * (0.2 * y + x)
x = x + h
Cells(i, 1) = x : Cells(i, 2) = y : i = i + 1
Loop While x<= xn
End Sub
Решение дифференциальных уравнений в приложении Mathcad. В приложении Mathcad решить дифференциальное уравнение можно, записав формулы выбранного метода. Например, для решения методом Эйлера уравнения
![]() x0
= 0, y0
= 1, h
=
0,1
x0
= 0, y0
= 1, h
=
0,1
на рабочем поле приложения Mathcad надо записать:
h := 0.1 n := 3 i := 0..n x0 := 0 y0 := 1
xi+1 = xi + h yi+1 = yi + h (0.2∙yi + xi)
x= y =
И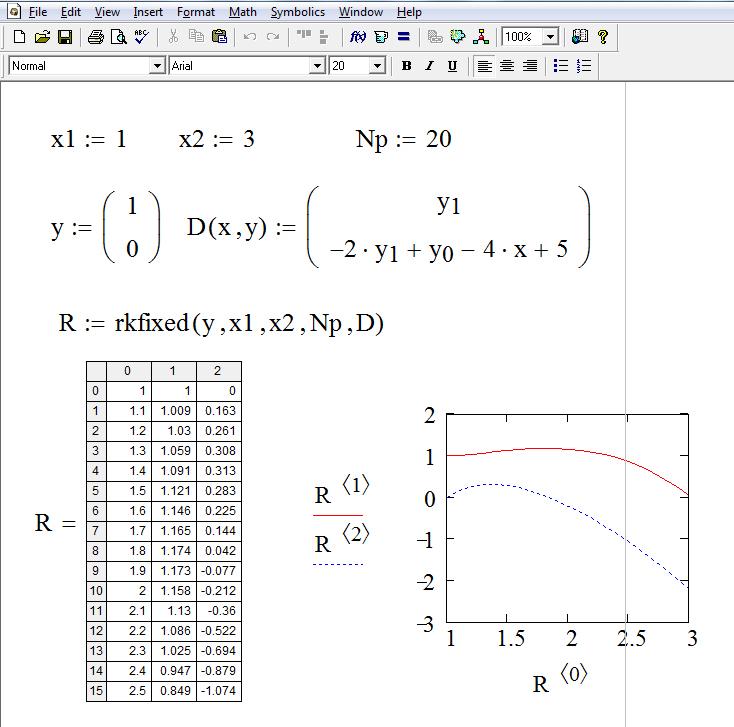 меются
также встроенные функции для решения
дифференциальных уравнений, например
функцияrkfixed.
меются
также встроенные функции для решения
дифференциальных уравнений, например
функцияrkfixed.
На рисунке приведена страница документа в приложении Mathcad с решением системы дифферен-циальных уравнений
![]()
![]()
на отрезке [1; 3].
Здесь x1, x2 – левая и правая границы интервала, на котором ищется решение; Np – число точек, в которых определяется решение; y0, y1 – начальные условия; D(x, y) – вектор правых частей системы.
На рисунке приведены также графики решения, характеризующие зависимость R(1, i) от R(0, i) и зависимость R(2, i) от R(0, i), т. е. зависимость y от x и зависимость z от x.
Назад
