Определим p1() и p0():

P₁() = ₁() – ₂(); P₀() = ₀() –₂().

С учетом ранее введенных определений

P₁() =  + 0(); P₀() = 1 –  + 0(). (2.5)

Подставим в систему уравнений (2.4) полученные значения вероятностей P₁() и P₀(). Затем, перенеся в левую часть уравнений P_k(t), поделим левые и правые части уравнения на . Переходя к пределу, получим

(2.6)

Решив систему дифференциальных уравнений, получим формулу Пуассона

. (2.7)

Таким образом, вероятность поступления точно k заявок простейшего потока за отрезок времени t определяется формулой Пуассона (2.7). По этой причине простейший поток также называют стационарным пуассоновским потоком.

Основные характеристики простейшего потока. При объединении n независимых простейших потоков c ₁, ₂, …, _n образуется простейший поток с параметром ₁ + ₂ + … + _n. Вероятность точно k заявок за отрезок времени t определяется формулой Пуассона

. (2.8)

Можно показать, что объединение большого числа независимых стационарных ординарных потоков с практически любым последействием при малых значениях параметров этих потоков создает общий поток, близкий к простейшему. Если каждый из потоков поступает от отдельного источника заявок, то простейший поток можно представить как поток от бесконечного числа источников, параметры каждого из которых стремятся к нулю.

Сумма вероятностей всех возможных значений числа поступающих заявок за рассматриваемый промежуток времени t равна 1. Действительно,

.

При t = 1 получаем

.

Функция P_k(t) есть функция распределения дискретной случайной величины K. Из (2.7) следует, что она зависит от t и k, а при t=1 –от  и k.

Как и для любой дискретной случайной величины, распределенной по закону Пуассона, математическое ожидание М(k) дисперсии D(k) и среднеквадратическое отклонение (k) числа заявок простейшего потока, поступивших за отрезок времени t, равны: M(k) = D(k) = t; (k) = . Приt = 1 M(k) = D(k) = , (k) = .

Из этого следует, что интенсивность простейшего потока равна его параметру  = M(k) = . Равенство  =  справедливо не только для простейшего потока, но и для любого стационарного ординарного потока.

Вероятность поступления k и более заявок определяется по формуле

.

Вероятности P_k(t) и P_ik(t) для различных значений k и t табулированы [11].

Функция F(z) распределения вероятностей промежутков времени между заявками. Согласно определению функция F(z) равна вероятности того, что промежуток времени между заявками будет меньше заданного промежутка z, что равносильно вероятности ₁(z) того, что за промежуток z поступит одна заявка и более. Используя (2.7), получим

F(z) = P(Z < z) = ₁(z) = ₀(z) – P₀(z) = 1 – e^–Z, z  0, (2.9)

а плотность распределения вероятности промежутков времени между заявками

. (2.10)

Таким образом, распределение промежутков времени между заявками простейшего потока подчиняется показательному (отрицательному экспоненциальному) закону. Функция F(z) зависит от параметра потока .

Характеристики промежутков времени между заявками Z можно записать в виде

, (2.11)

, (2.12)

. (2.13)

Из (2.11) и (2.13) следует, что M(z) = (z). Такое равенство характерно для показательного закона распределения любой случайной величины. Формула (2.11) показывает, что с увеличением параметра потока  уменьшается математическое ожидание промежутка времени между заявками M(z).

Распределение промежутков времени между заявками по показательному закону (2.9) является не только необходимым, но и достаточным условием существования простейшего потока. Можно показать, что поток с независимыми промежутками между заявками, распределенными по одинаковому показательному закону (2.9), является простейшим потоком.

Показательный закон обладает следующим свойством: если промежуток времени, распределенный по показательному закону, уже длится некоторое время, то это никак не влияет на закон распределения оставшейся части промежутка; он будет таким же, как и закон распределения всего промежутка. Для доказательства предположим, что промежуток времени между заявками равен t. Найдем по условию вероятность того, что он будет продолжаться еще не менее времени . На основании теоремы умножения вероятностей можно записать

P(z > t + ) = P(z > t) P(z > /z > t).

С учетом (2.9)

e^{–(t+)} = e^– P(z > /z > t),

откуда условная вероятность

P(z > /z > t) = e^– = P(z > ),

т.е. она не зависит от уже длившейся части времени обслуживания и равна безусловной вероятности P(z > ), что и требовалось доказать.

Показательный закон – единственный, обладающий таким свойством. Это свойство показательного закона представляет собой, в сущности, другую формулировку основного свойства простейшего потока – отсутствие последействия. Такое замечательное свойство показательного распределения позволяет упростить математические преобразования, в частности, при анализе процесса поступления заявок и их обслуживания.

2.5. Нестационарный и неординарный пуассоновские потоки

Нестационарный пуассоновский поток (который также называется потоком с переменными параметрами или нестационарным простейшим потоком) есть ординарный поток без последействия, для которого в любой момент времени t существует конечный параметр (t), зависящий от момента t. По аналогии с простейшим потоком в качестве математической модели нестационарного пуассоновского потока выбирается вероятность Р_k(t₀, t) поступления точно k вызовов за данный промежуток времени [t₀, t). В силу нестационарности потока эта вероятность зависит не только от длины промежутка времени [t₀, t), но и от начального момента t₀.

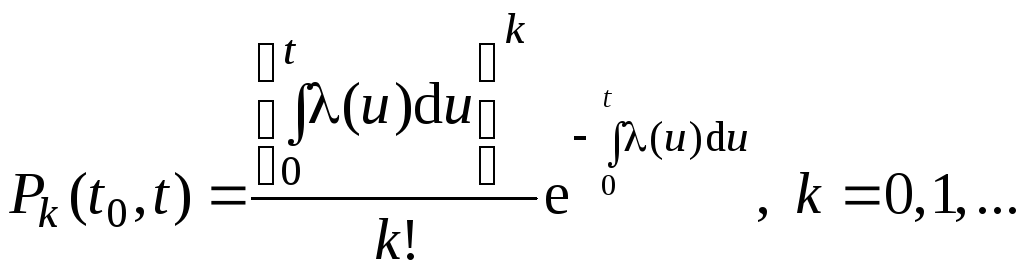(2.14)

Заметим, что для стационарного потока (n)=, (и формула (2.14) преобразуется в (2.7)).

Для неординарного потока, т.е. для стационарного неординарного потока без последействия, следует различать поток вызывающих моментов и поток заявок. Поток вызывающих моментов характеризуется вероятностью появления точно i вызывающих моментов в промежутке времени t. Эта вероятность P_i(t) определяется формулой Пуассона (2.7).

В каждый вызывающий момент поступает l (1  l  r) заявок. Величина l называется характеристикой неординарного потока, может быть постоянной и переменной. Если l = const, то с вероятностью P_i(t) суммарное число заявок, поступающих за отрезок времени t, составляет k = l_i.

Для неординарного пуассоновского потока с переменной величиной l, в котором в каждый вызывающий момент с вероятностью _i поступает l заявок (), также получена формула, определяющая вероятностьP_k(t) поступления точно k заявок за промежуток времени t (см. работу [6]). Параметр такого потока для каждого значения l равен _i. Отсюда общий параметр для потока () такой же, как и для потока вызывающих моментов, т.е. для простейшего потока. Интенсивность неординарного пуассоновского потока, как и любого стационарного неординарного потока, больше его параметра . Действительно,

.

2.6. Потоки с простым последействием

Основной характеристикой потока с простым последействием является зависимость параметра потока от состояния системы массового обслуживания в любой момент времени t. Под параметром потока в некотором состоянии S(t) будем понимать предел

, (2.15)

где ₁(t, t + /S(t)) – вероятность поступления за промежуток [t, t + r) одной заявки и более, если в момент t система находилась в состоянии S(t). Это определение позволяет сформулировать понятие потока с простым последействием. Под потоком с простым последействием понимается ординарный поток, для которого в любой момент времени t существует конечный параметр потока в состоянии S(t) (2.15), зависящий только от состояния S(t) системы в момент t и не зависящий от процесса обслуживания заявок до момента t.

Параметр потока с простым последействием в любой момент времени t зависит от состояния системы в этот момент времени, а состояние системы S(t), в свою очередь, зависит от процесса поступления и обслуживания заявок до момента t. Такое последействие принято называть простым, поскольку для определения параметра потока в момент t достаточно ограничиться значением состояния системы S(t) в этот момент времени. Поток с простым последействием является нестандартным, так как его параметр зависит от момента t. Заметим, что эта зависимость проявляется через состояние S(t). Для каждого конкретного состояния параметр потока с простым последействием является постоянной величиной.

Понятие потока с простым последействием – одно из самых общих в теории потоков. Практически любой поток заявок можно считать потоком с простым последействием, поскольку обслуживающая система всегда влияет на процесс поступления заявок. К частным случаям потока с простым последействием относятся симметричный поток, примитивный поток и поток с повторными заявками.