Вектор, обладающий свойствами (2.20) и (2.21), называется стохастическим. Если его компоненты представляют вероятности состояний системы, то вектор называется вектором состояний системы.
Предположим, что
переход из одного состояния в другое
зависит только от этих двух состояний.
Более строго, предположим, что каждой
паре (En,
)
можно поставить в соответствие условную
вероятность
того, что система находится в состоянииn1
в момент i
+ 1 при условии, что она находилась в
состоянии n
в момент i.
Считая, что начальные вероятности Pn(0)
известны, получим цепь Маркова, вектор
состояний которой удовлетворяет
уравнениям
,
(2.22)
или в матричных обозначениях
P(i + 1) = P(i)F (2.23)
(квадратная матрица F образована из элементов Pnn1, удовлетворяющих условиям
0
1 для всех n
и n1
(2.24)
и
для
всех n).
(2.25)
Всякая матрица,
обладающая свойствами (2.24) и (2.25),
называется стохастической; каждая ее
сторона представляет стохастический
вектор. Вероятности
называются вероятностями перехода,
сама стохастическая матрица часто
называется матрицей (вероятностей)
перехода.
Цепь Маркова полностью определяется стохастической матрицей F и совокупностью начальных вероятностей состояний Pn(0).
Матрица перехода
F
может зависеть от времени, т.е. вероятности
перехода
могут быть функциямиi,
тогда
где
Pn(0)
и
(i)
заданы.
Такая цепь называется неоднородной.
Наличие в матрице
перехода элемента
,
не равного нулю, указывает на то, что
переходEn
возможен. Рассмотрим несколько примеров
цепей Маркова.
Пример 2.3. Имеются три лотерейных круга А, В и С [2.8], каждый из которых разбит на три неравных сектора А, В и С, которые также обозначены буквами А, B и С (рис. 2.3).
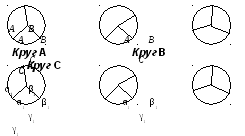
Рис. 2.3. Пример, иллюстрирующий цепь Маркова
У каждого круга с параметром n (n = 1, 2, 3) центральные углы n, n и n, соответствующие трем секторам, измерены в таких единицах, что n + + n + n = 1. Производится серия испытаний, из которых начальное (нулевое) состоит в том, что случайным равновероятным образом выбирается один из кругов и этот круг приводится во вращение. Следующее испытание проводится с кругом, определенным в результате первого испытания. Назовем состоянием системы в момент i результат i-го испытания, обозначаемый одним из чисел 1, 2 или 3. Тогда получается цепь Маркова с начальными вероятностями (т.е. вероятностями в момент 0):
P1(0) = 1/3(1 + 2 + 3),
P2(0) = 1/3(1 + 2 + 3),
P3(0) = 1/3(1 + 2 + 3),
где 1 + 1 + 1 = 1, 2 + 2 + 2 = 1, 3 + 3 + 3 = 1.
Матрица перехода имеет вид
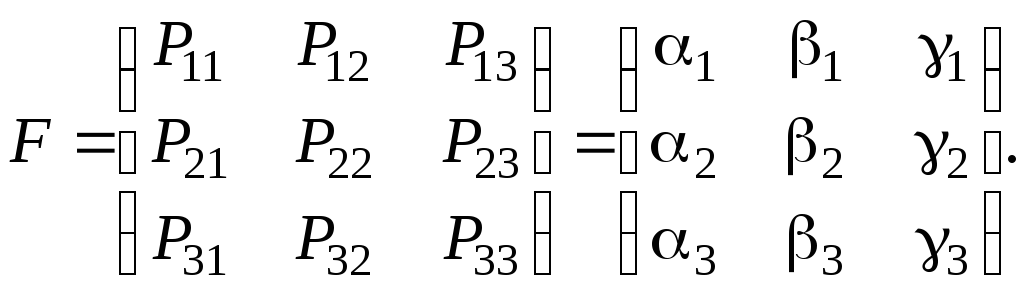
После первого испытания вероятности состояний равны:
(P1(1); P2(1); P3(1)) = (P1(0); P2(0); P3(0))F = 1P1(0) 2P2(0) + 3P3(0);
1P1(0) + 2P2(0) + 3P3(0); 1P1(0)+2P2(0)+3P3(0).
На рис. 2.4 представлен граф возможных переходов с соответствующими вероятностями.
Рис. 2.4. Граф перехода к примеру 2.3
Например,
P2(1) = 1/3{(1 + 2 + 3) 1 + (1 + 2 + 3) 2 + (1 + 2 + 3) 3}.
Предположим, что результатом i-го испытания является состояние А; посмотрим, какова в этом случае вероятность перейти в состояние А в (i+2)-м испытании. Рассматривая i-е испытание как начальное, имеем
(P1(2); P2(2); P3(2)) = (1; 0; 0) F2 = (12 + 12 + 13;
11 + 12 + 13; 1 1 + 11 + 13).
Следовательно,
.
Пример 2.4. Эскадрилья бомбардировщиков [13] насчитывает 4 самолета. Как правило, эскадрилья получает боевое задание один раз в день. Если к концу дня наличный состав уменьшается до 0; 1 или 2 самолетов из-за потерь, нанесенных противником, командир эскадрильи получает 1 самолет из резерва; этот самолет ему доставляют ночью. Если наличный состав остается равным 3 или 4 самолетам, то командир не имеет права на пополнение. На следующий день, если в наличии имеется 3 или 4 самолета, задание эскадрилье дается, в противном случае задание отменяется. Во время выполнения задания каждый самолет может быть выведен из строя с вероятностью Р.
Если на задание посылается n самолетов, вероятность того, что k из них будут выведены из строя, задается биномиальным распределением
.
Граф переходов показан на рис. 2.5; здесь имеется цепь Маркова с матрицей
в момент i+1
где
q
= 1 –p
в
момент i
Рис. 2.5. Граф перехода к примеру 2.4
Первая строка матрицы относится к случаю, когда в момент i имеется один самолет; тогда в момент i+1 в наличии будут два самолета, потому что будет получено пополнение (1 самолет) и не будет вылета на задание. Вторая строка представляет состояние 2 (2 самолета) в момент i; в этом случае также не будет вылета и будет пополнение. Третья строка изображает состояние 3 в момент i; очевидно, в этом случае состоится боевой вылет группы в составе 3 самолетов; вероятность того, что к моменту i+1 будет 1 самолет, соответствуют случаю, когда ни один самолет не вернется, следовательно, р31 = р3; вероятность того, что к моменту i+1 будет 2 самолета, соответствует случаю, когда с задания вернется 1 самолет, т.е. p32 = = 3p2q; вероятность того, что в момент i = 1 будет 3 самолета, соответствует случаю возвращения 2 или 3 самолетов, откуда p33 = 3pq2 + q3. Аналогичными рассуждениями можно найти элементы четвертой строки рассматриваемой матрицы.