Частные производные. Применение дифференциального исчисления в теории ошибок измерений.

1.D = .

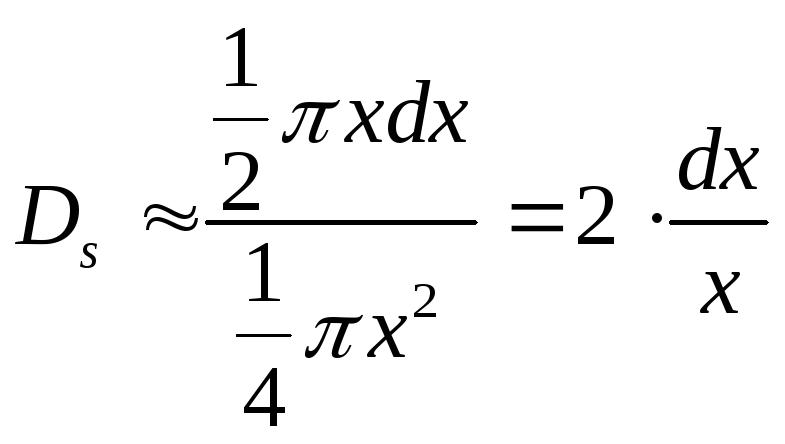2. Относительная погрешность вычисленной площади , а её приближённое значение мы получим, заменив в этом равенстве ∆S на dS. В таком случае . Но площадь круга(x-диаметр), а поэтому . Таким образом. (Иначе:).По условию x = 6,7 см; dx = 0,03 см, а потому, а умножая эту величину на 100, получим погрешность в процентах, которая равна (0,009 · 100)% = 0,9%.

3.Объём шара вычисляется по формуле, гдеx- диаметр шара. Приближённо погрешность ∆V вычисленного объёма (приращение объёма как функции диаметра) равна. Относительная погрешность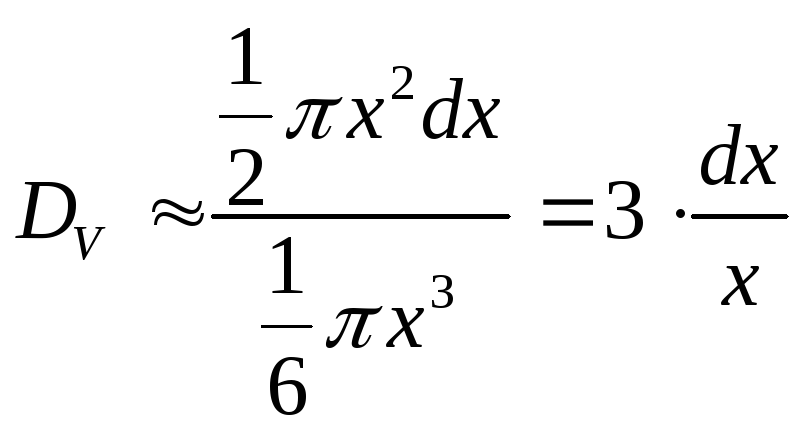. Но относительна погрешность измерения диаметра, а поэтому, что и требовалось доказать.

4.D_R = 0,66%.

5.поэтому относительная погрешностьD_T=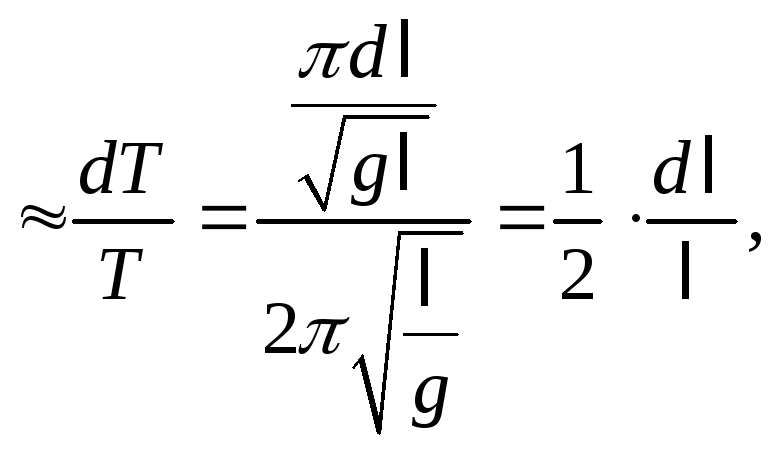а так как относительная погрешность измерения длины маятникаD_l≈тоD_TD_l.

6.Задача состоит в определении приращения периода как функции приращения длины маятника. Вспомнив, что дифференциал функции является главной частью приращения функции, легко получить ответ, найдя дифференциал периода по переменной - длине маятника.) =Перейдя к конечным приращениям получим приближённую формулу:. Далее:. Длину маятника следует увеличить на 2,5 см.

7.Условие задачи позволяет считатьgфункцией только длины.

8.D_g = 2D_T; 9. 10.11.;12.

13.;14. 15. ; 16.17.18.

19.«Градиент» скорости и скорость сдвига.

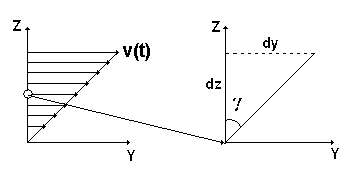
«Градиент» скорости , входящий в формулу закона Ньютона для вязкой жидкости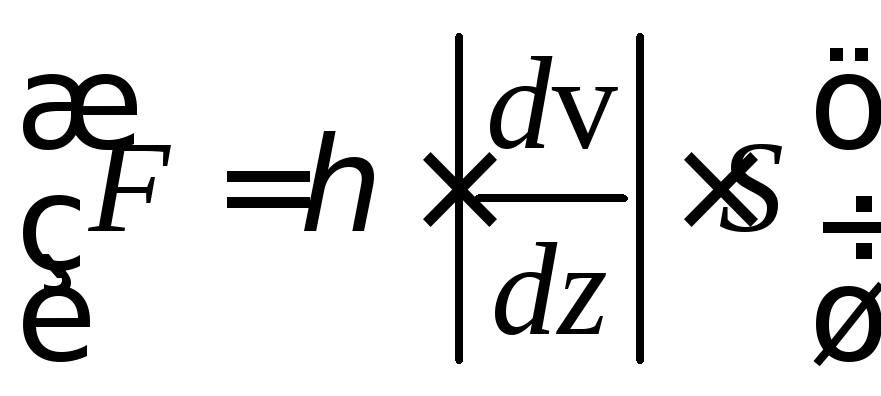, как это видно из рисунка, представляет собой, с математической точки зрения, смешанную производную от координатыyпо аргументамzиt. Обоснованно предположив независимость аргументов и непрерывность частных производных по этим аргументам получим: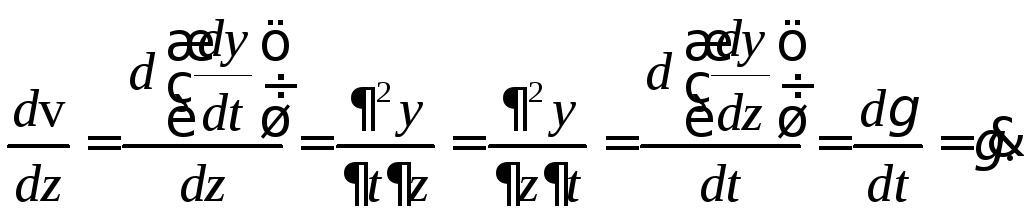в физике называют скоростью деформации сдвига (скоростью сдвига) и эта величина измеряетсяили обратными секундами. Иначе говоря, скорость деформации при простом сдвигеравна градиенту скорости течения.

Скалярное поле. Производные по направлению. Градиент.

1.Полагаяu=1, 2, 3, 4, 5, получим уравнения соответствующих линий уровня:

x + y = 1; x + y = 2; x + y = 3; x + y = 4; x + y = 5.

Построив эти линии в прямоугольной системе координатx0y, получим прямые, параллельные биссектрисе 2 – го и 4 - го координатных углов.

2.Написав уравнения линий уровня:x²+y²=1,x²+y²=2,x²+y²=3,x²+y²=4,x²+y²=5 и построив их в плоскостиx0y, получим концентрические окружности с центром в начале координат.

3.Линии уровня 2y=x²,y=x², 2y= 3x²,y= 2x², 2y= 5x²представляют параболы, симметричные оси 0yс общей вершиной в начале координат.

4.Находим частные производные функцииuи вычисляем их значения в точке А:

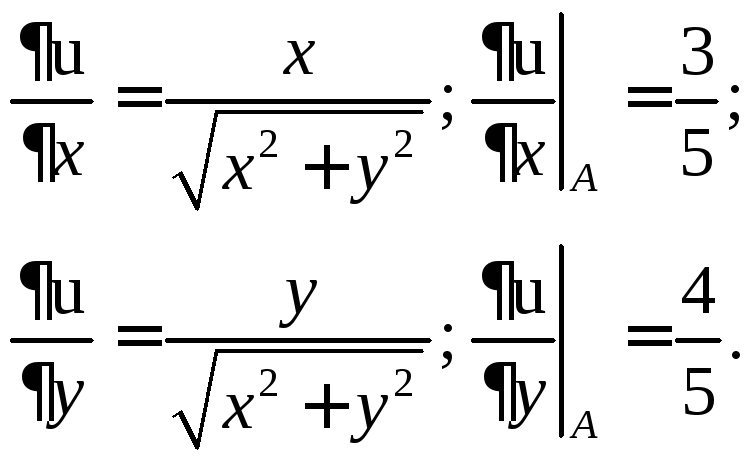
Подставляя в формулу: найдём производную функцииuв точкеAпо любому направлению

Находим далее косинусы углов α и β, образованныхзаданным направлением дифференцирования с осями координат, и производную функцииuпо заданному направлению.

Для биссектрисы первого координатного угла: α = β = 45⁰_, cosα =cosβ =

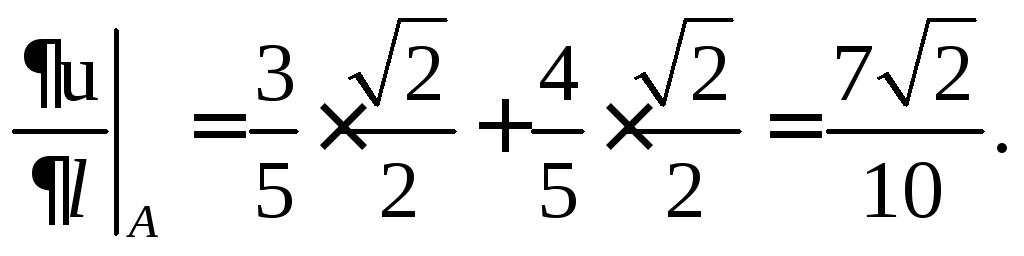
5.Находим частные производные функцииuи вычисляем их значения в точке А:

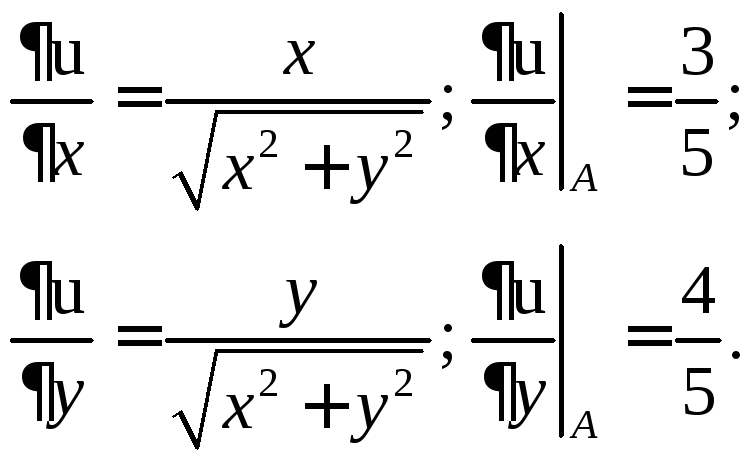
Подставляя в формулу найдём производную функцииuв точкеAпо любому направлению

Находим далее косинусы углов α и β, образованныхзаданным направлением дифференцирования с осями координат, и производную функцииuпо заданному направлению.

Для вектора :_, cosα =cosβ =

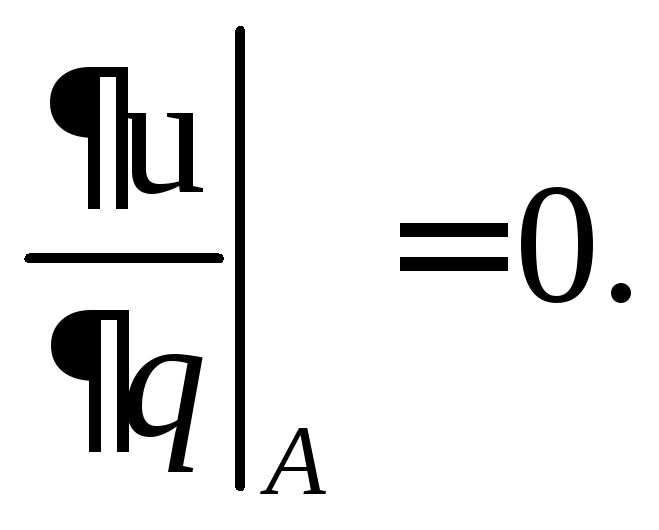
6.Находим частные производные функцииuи вычисляем их значения в точке А:

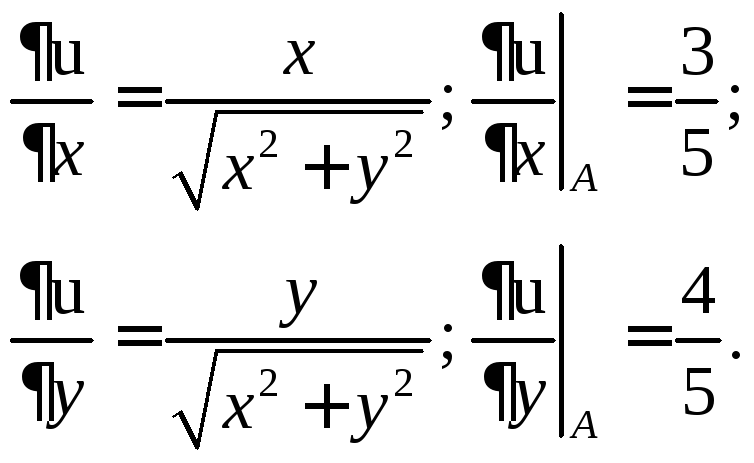
Подставляя в формулу: найдём производную функцииuв точкеAпо любому направлению

Находим далее косинусы углов α и β, образованныхзаданным направлением дифференцирования с осями координат, и производную функцииuпо заданному направлению.

Для вектора :_, cosα =cosβ =

7.Наибольшая по абсолютной величине скорость изменения (возрастания или убывания) функцииu(M) при переходе точкиMв точкуPчисленно равна модулю градиента функции в точкеP. При этом функция,будет возрастать или убывать с наибольшей скоростью, смотря по тому, будет ли точкаMпри переходе через точкуPдвигаться по направлению градиента функции в точкеPили по прямо противоположному направлению.

Руководствуясь этими положениями, находим частные производные функции uи по формуле ─ её градиент в любой точке:

Далее находим:

1)

2) его модуль, численно равный искомой наибольшей скорости возрастания функции u(M)при переходе М через М₀, будет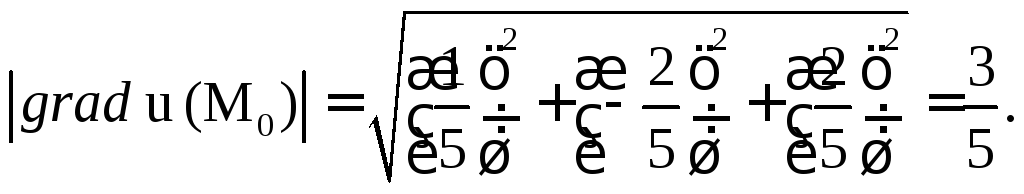

8.Наибольшая по абсолютной величине скорость изменения (возрастания или убывания) функцииu(M) при переходе точкиMв точкуPчисленно равна модулю градиента функции в точкеP. При этом функция, будет возрастать или убывать с наибольшей скоростью, смотря по тому, будет ли точкаMпри переходе через точкуPдвигаться по направлению градиента функции в точкеPили по прямо противоположному направлению.

Руководствуясь этими положениями, находим частные производные функции uи по формуле ─её градиент в любой точке:

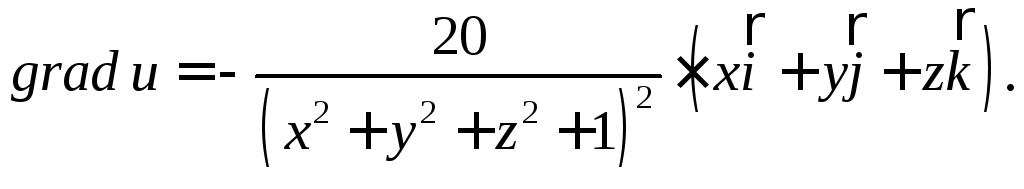Далее находим:

1)

2) искомый вектор, имеющий прямо противоположное направление, будет

─

Чтобы функция u(M) убывала с наибольшей скоростью, при переходе через точкуM₁точкаMдолжна двигаться в направлении ─

9.Чтобы в некоторой точкеPпроизводная функции по любому направлению была равна нулю, необходимо и достаточно, чтобы в этой точке все частные производные первого порядка функции одновременно обращались в нуль. [Согласно формуле:.]

Поэтому, найдя частные производные:

и и решая систему уравненийи, получим две точки: (-3, 1) и (1, -1), в которых функция стационарна.

10.Поверхностями уровня данного поля являются концентрические сферы с центром в начале координат:x²+y²+z²= С.

11.

12.Найдём единичный вектор:

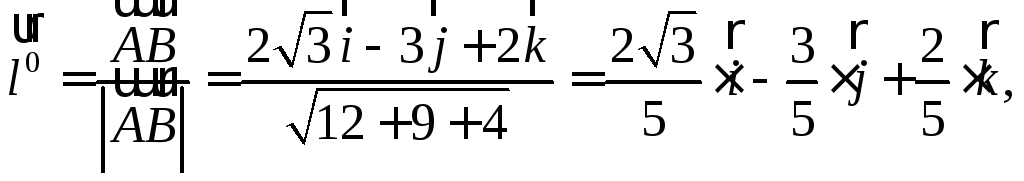
а затем производную скалярного поля Uпо направлению векторав точке А:

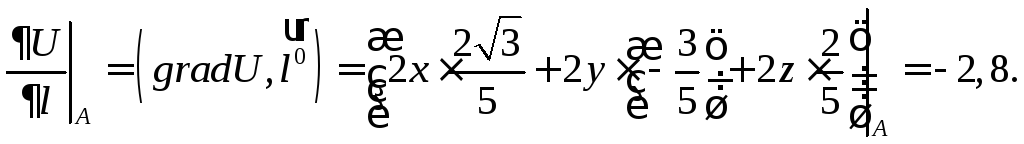
Так как то данное скалярное поле убывает в направлении вектора.

13. 1). Воспользуемся определением градиента скалярной функции:

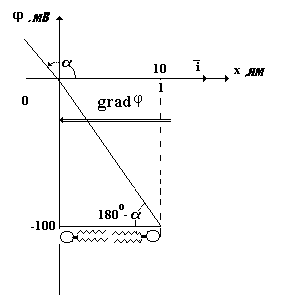
2). Направим ось x поперёк мембраны снаружи внутрь. Учтём, что вданном случае, потенциал – скалярная функция только одной координаты х, тогда:. 3). Изобразим график зависимости потенциала от координатыx.

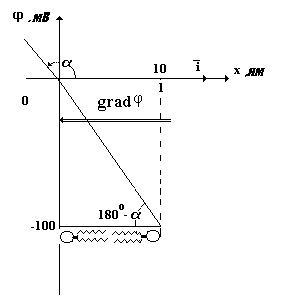
4). По графику можно определить tgα. Видно, что он отрицательный и по определению равен производной потенциала по координате x. Вычислим производную.

5). , т.е. вектор градиент потенциала направлен наружу клетки и по модулю равен

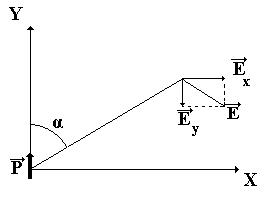
_14.По известному выражению для потенциала поля точечного электростатического диполянайдём модуль напряжённости поля. При этом учтём, что особым выделенным направлением в данном случае окажется направление, совпадающее с направлением дипольного моментаP. Если расположить диполь в пространстве так, что он находится в начале координат и направлен вдоль осиY, то картина силовых линий поля диполя окажется одинаковой для любой плоскости, проходящей через вектор дипольного момента.φи Ε симметричны относительно осиY.

Воспользуемся связью напряжённости электростатического поля с его потенциалом и найдём проекции вектора напряжённости

и . После чего модуль вектора напряженности получится как:.

На плоскости XY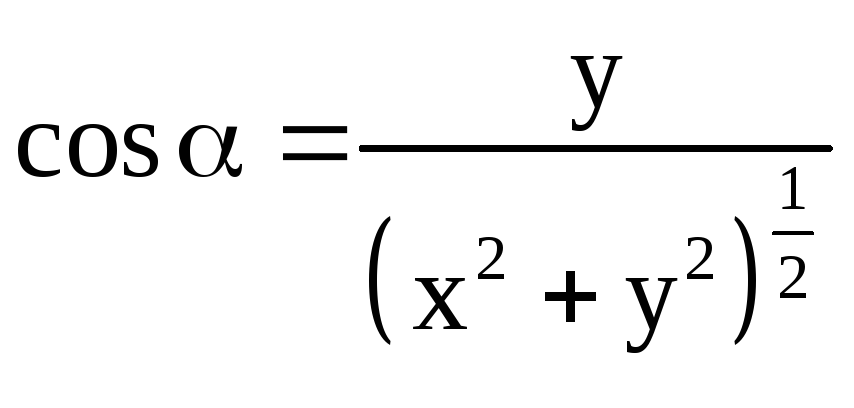,и.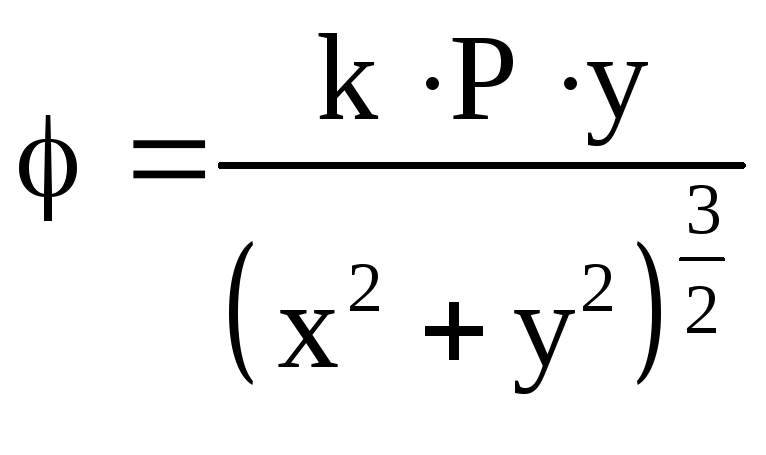

Для проекции получим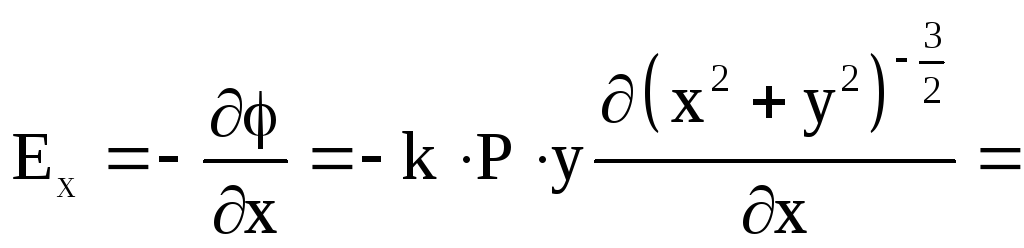

.

Для проекции получим:

.

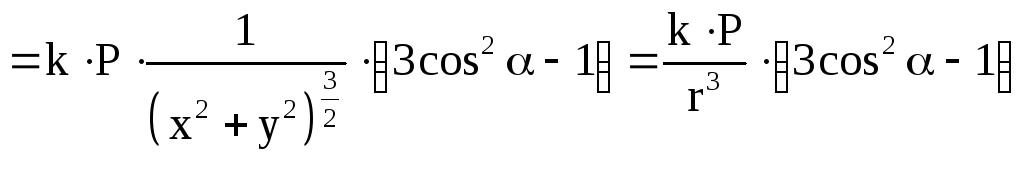Итак:,иначе.